Considering Perspectives for Automated Driving Ethics: Collective Risk in Vehicular Motion Planning

Recent automated vehicle (AV) motion planning strategies evolve around minimizing risk in road traffic. However, they exclusively consider risk from the AV's perspective and, as such, do not address the ethicality of its decisions for other road users. We argue that this does not reduce the risk of each road user, as risk may be different from the perspective of each road user. Indeed, minimizing the risk from the AV's perspective may not imply that the risk from the perspective of other road users is also being minimized; in fact, it may even increase. To test this hypothesis, we propose an AV motion planning strategy that supports switching risk minimization strategies between all road user perspectives. We find that the risk from the perspective of other road users can generally be considered different to the risk from the AV's perspective. Taking a collective risk perspective, i.e., balancing the risks of all road users, we observe an AV that minimizes overall traffic risk the best, while putting itself at slightly higher risk for the benefit of others, which is consistent with human driving behavior. In addition, adopting a collective risk minimization strategy can also be beneficial to the AV's travel efficiency by acting assertively when other road users maintain a low risk estimate of the AV. Yet, the AV drives conservatively when its planned actions are less predictable to other road users, i.e., associated with high risk. We argue that such behavior is a form of self-reflection and a natural prerequisite for socially acceptable AV behavior. We conclude that to facilitate ethicality in road traffic that includes AVs, the risk-perspective of each road user must be considered in the decision-making of AVs.

Risk Estimation for Automated Driving

Safety is a central requirement for automated vehicles. As such, the assessment of risk in automated driving is key in supporting both motion planning technologies and safety evaluation. In automated driving, risk is characterized by two aspects. The first aspect is the uncertainty on the state estimates of other road participants by an automated vehicle. The second aspect is the severity of a collision event with said traffic participants. Here, the uncertainty aspect typically causes the risk to be non-zero for near-collision events. This makes risk particularly useful for automated vehicle motion planning. Namely, constraining or minimizing risk naturally navigates the automated vehicle around traffic participants while keeping a safety distance based on the level of uncertainty and the potential severity of the impending collision. Existing approaches to calculate the risk either resort to empirical modeling or severe approximations, and, hence, lack generalizability and accuracy. In this paper, we combine recent advances in collision probability estimation with the concept of collision severity to develop a general method for accurate risk estimation. The proposed method allows us to assign individual severity functions for different collision constellations, such as, e.g., frontal or side collisions. Furthermore, we show that the proposed approach is computationally efficient, which is beneficial, e.g., in real-time motion planning applications. The programming code for an exemplary implementation of Gaussian uncertainties is also provided.

Collision Probability Estimation for Optimization-based Vehicular Motion Planning

Many motion planning algorithms for automated driving require estimating the probability of collision (POC) to account for uncertainties in the measurement and estimation of the motion of road users. Common POC estimation techniques often utilize sampling-based methods that suffer from computational inefficiency and a non-deterministic estimation, i.e., each estimation result for the same inputs is slightly different. In contrast, optimization-based motion planning algorithms require computationally efficient POC estimation, ideally using deterministic estimation, such that typical optimization algorithms for motion planning retain feasibility. Estimating the POC analytically, however, is challenging because it depends on understanding the collision conditions (e.g., vehicle's shape) and characterizing the uncertainty in motion prediction. In this paper, we propose an approach in which we estimate the POC between two vehicles by over-approximating their shapes by a multi-circular shape approximation. The position and heading of the predicted vehicle are modelled as random variables, contrasting with the literature, where the heading angle is often neglected. We guarantee that the provided POC is an over-approximation, which is essential in providing safety guarantees, and present a computationally efficient algorithm for computing the POC estimate for Gaussian uncertainty in the position and heading. This algorithm is then used in a path-following stochastic model predictive controller (SMPC) for motion planning. With the proposed algorithm, the SMPC generates reproducible trajectories while the controller retains its feasibility in the presented test cases and demonstrates the ability to handle varying levels of uncertainty.

Predicting the Influence of Adverse Weather on Pedestrian Detection with Automotive Radar and Lidar Sensors

Pedestrians are among the most endangered traffic participants in road traffic. While pedestrian detection in nominal conditions is well established, the sensor and, therefore, the pedestrian detection performance degrades under adverse weather conditions. Understanding the influences of rain and fog on a specific radar and lidar sensor requires extensive testing, and if the sensors' specifications are altered, a retesting effort is required. These challenges are addressed in this paper, firstly by conducting comprehensive measurements collecting empirical data of pedestrian detection performance under varying rain and fog intensities in a controlled environment, and secondly, by introducing a dedicated Weather Filter (WF) model that predicts the effects of rain and fog on a user-specified radar and lidar on pedestrian detection performance. We use a state-of-the-art baseline model representing the physical relation of sensor specifications, which, however, lacks the representation of secondary weather effects, e.g., changes in pedestrian reflectivity or droplets on a sensor, and adjust it with empirical data to account for such. We find that our measurement results are in agreement with existent literature related to weather degredation and our WF outperforms the baseline model in predicting weather effects on pedestrian detection while only requiring a minimal testing effort.

Fast Collision Probability Estimation for Automated Driving using Multi-circular Shape Approximations

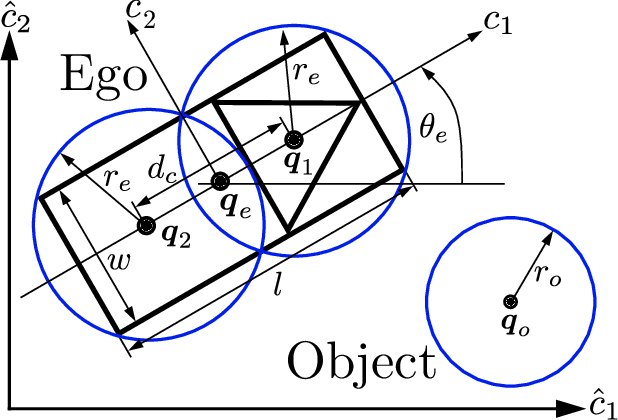
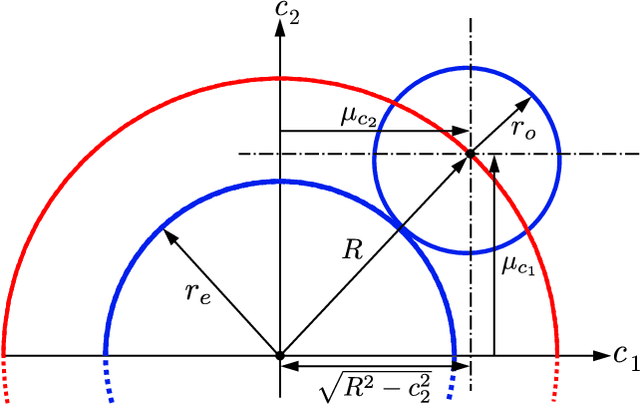
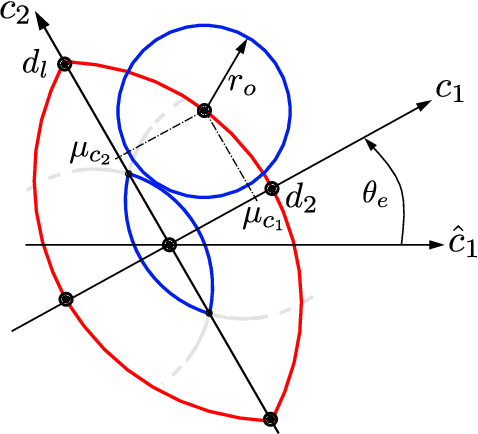
Many state-of-the-art methods for safety assessment and motion planning for automated driving require estimation of the probability of collision (POC). To estimate the POC, a shape approximation of the colliding actors and probability density functions of the associated uncertain kinematic variables are required. Even with such information available, the derivation of the POC is in general, i.e., for any shape and density, only possible with Monte Carlo sampling (MCS). Random sampling of the POC, however, is challenging as computational resources are limited in real-world applications. We present expressions for the POC in the presence of Gaussian uncertainties, based on multi-circular shape approximations. In addition, we show that the proposed approach is computationally more efficient than MCS. Lastly, we provide a method for upper and lower bounding the estimation error for the POC induced by the used shape approximations.