Sonja Füllhase
Graph Isomorphic Networks for Assessing Reliability of the Medium-Voltage Grid
Oct 03, 2023Abstract:Ensuring electricity grid reliability becomes increasingly challenging with the shift towards renewable energy and declining conventional capacities. Distribution System Operators (DSOs) aim to achieve grid reliability by verifying the n-1 principle, ensuring continuous operation in case of component failure. Electricity networks' complex graph-based data holds crucial information for n-1 assessment: graph structure and data about stations/cables. Unlike traditional machine learning methods, Graph Neural Networks (GNNs) directly handle graph-structured data. This paper proposes using Graph Isomorphic Networks (GINs) for n-1 assessments in medium voltage grids. The GIN framework is designed to generalise to unseen grids and utilise graph structure and data about stations/cables. The proposed GIN approach demonstrates faster and more reliable grid assessments than a traditional mathematical optimisation approach, reducing prediction times by approximately a factor of 1000. The findings offer a promising approach to address computational challenges and enhance the reliability and efficiency of energy grid assessments.
Adaptive Blending Units: Trainable Activation Functions for Deep Neural Networks
Jun 26, 2018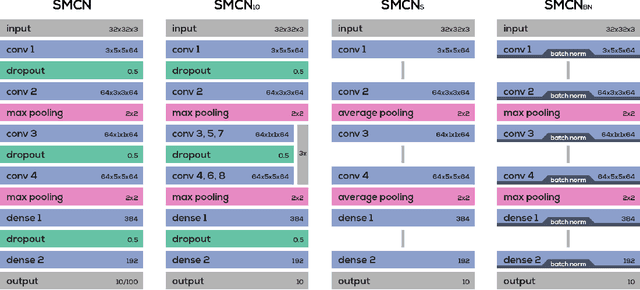
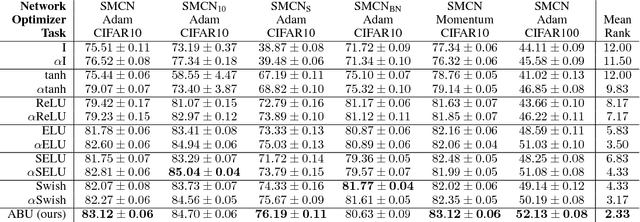
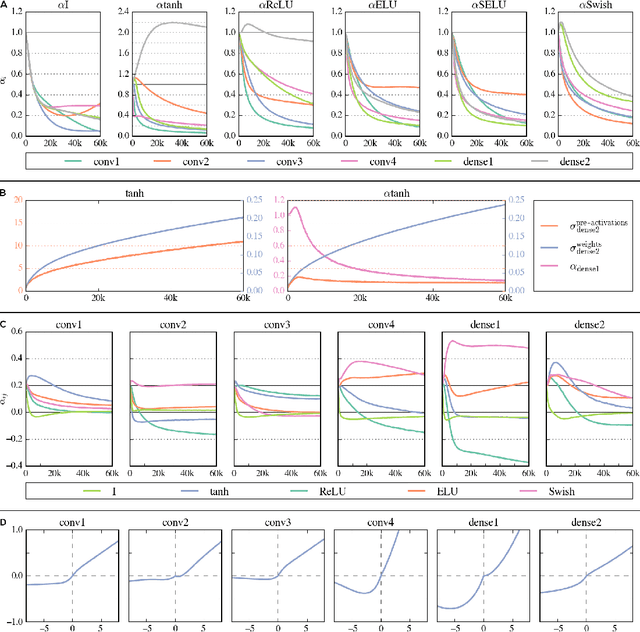

Abstract:The most widely used activation functions in current deep feed-forward neural networks are rectified linear units (ReLU), and many alternatives have been successfully applied, as well. However, none of the alternatives have managed to consistently outperform the rest and there is no unified theory connecting properties of the task and network with properties of activation functions for most efficient training. A possible solution is to have the network learn its preferred activation functions. In this work, we introduce Adaptive Blending Units (ABUs), a trainable linear combination of a set of activation functions. Since ABUs learn the shape, as well as the overall scaling of the activation function, we also analyze the effects of adaptive scaling in common activation functions. We experimentally demonstrate advantages of both adaptive scaling and ABUs over common activation functions across a set of systematically varied network specifications. We further show that adaptive scaling works by mitigating covariate shifts during training, and that the observed advantages in performance of ABUs likewise rely largely on the activation function's ability to adapt over the course of training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge