Genesis: Towards the Automation of Systems Biology Research

The cutting edge of applying AI to science is the closed-loop automation of scientific research: robot scientists. We have previously developed two robot scientists: `Adam' (for yeast functional biology), and `Eve' (for early-stage drug design)). We are now developing a next generation robot scientist Genesis. With Genesis we aim to demonstrate that an area of science can be investigated using robot scientists unambiguously faster, and at lower cost, than with human scientists. Here we report progress on the Genesis project. Genesis is designed to automatically improve system biology models with thousands of interacting causal components. When complete Genesis will be able to initiate and execute in parallel one thousand hypothesis-led closed-loop cycles of experiment per-day. Here we describe the core Genesis hardware: the one thousand computer-controlled $\mu$-bioreactors. For the integrated Mass Spectrometry platform we have developed AutonoMS, a system to automatically run, process, and analyse high-throughput experiments. We have also developed Genesis-DB, a database system designed to enable software agents access to large quantities of structured domain information. We have developed RIMBO (Revisions for Improvements of Models in Biology Ontology) to describe the planned hundreds of thousands of changes to the models. We have demonstrated the utility of this infrastructure by developed two relational learning bioinformatic projects. Finally, we describe LGEM+ a relational learning system for the automated abductive improvement of genome-scale metabolic models.

The Use of AI-Robotic Systems for Scientific Discovery

The process of developing theories and models and testing them with experiments is fundamental to the scientific method. Automating the entire scientific method then requires not only automation of the induction of theories from data, but also experimentation from design to implementation. This is the idea behind a robot scientist -- a coupled system of AI and laboratory robotics that has agency to test hypotheses with real-world experiments. In this chapter we explore some of the fundamentals of robot scientists in the philosophy of science. We also map the activities of a robot scientist to machine learning paradigms, and argue that the scientific method shares an analogy with active learning. We demonstrate these concepts using examples from previous robot scientists, and also from Genesis: a next generation robot scientist designed for research in systems biology, comprising a micro-fluidic system with 1000 computer-controlled micro-bioreactors and interpretable models based in controlled vocabularies and logic.

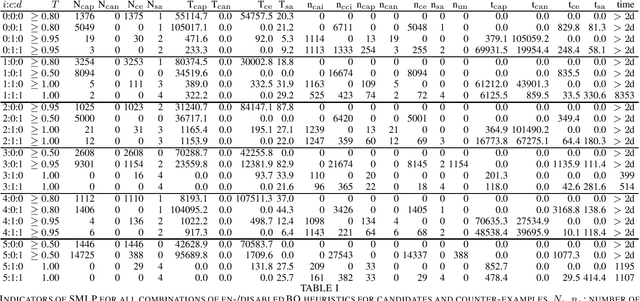
SMLP: Symbolic Machine Learning Prover

Symbolic Machine Learning Prover (SMLP) is a tool and a library for system exploration based on data samples obtained by simulating or executing the system on a number of input vectors. SMLP aims at exploring the system based on this data by taking a grey-box approach: SMLP combines statistical methods of data exploration with building and exploring machine learning models in close feedback loop with the system's response, and exploring these models by combining probabilistic and formal methods. SMLP has been applied in industrial setting at Intel for analyzing and optimizing hardware designs at the analog level. SMLP is a general purpose tool and can be applied to systems that can be sampled and modeled by machine learning models.

Machine Learning Meets The Herbrand Universe

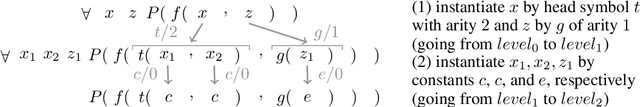
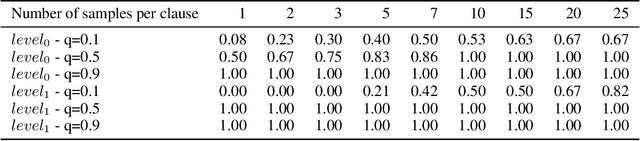
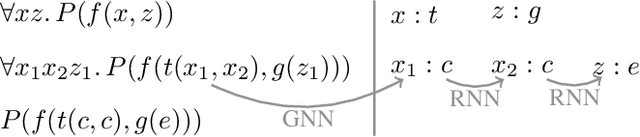
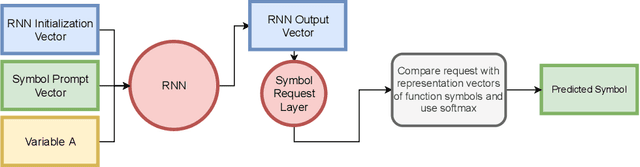
The appearance of strong CDCL-based propositional (SAT) solvers has greatly advanced several areas of automated reasoning (AR). One of the directions in AR is thus to apply SAT solvers to expressive formalisms such as first-order logic, for which large corpora of general mathematical problems exist today. This is possible due to Herbrand's theorem, which allows reduction of first-order problems to propositional problems by instantiation. The core challenge is choosing the right instances from the typically infinite Herbrand universe. In this work, we develop the first machine learning system targeting this task, addressing its combinatorial and invariance properties. In particular, we develop a GNN2RNN architecture based on an invariant graph neural network (GNN) that learns from problems and their solutions independently of symbol names (addressing the abundance of skolems), combined with a recurrent neural network (RNN) that proposes for each clause its instantiations. The architecture is then trained on a corpus of mathematical problems and their instantiation-based proofs, and its performance is evaluated in several ways. We show that the trained system achieves high accuracy in predicting the right instances, and that it is capable of solving many problems by educated guessing when combined with a ground solver. To our knowledge, this is the first convincing use of machine learning in synthesizing relevant elements from arbitrary Herbrand universes.

Bayesian Optimisation with Formal Guarantees

Application domains of Bayesian optimization include optimizing black-box functions or very complex functions. The functions we are interested in describe complex real-world systems applied in industrial settings. Even though they do have explicit representations, standard optimization techniques fail to provide validated solutions and correctness guarantees for them. In this paper we present a combination of Bayesian optimisation and SMT-based constraint solving to achieve safe and stable solutions with optimality guarantees.

Premise selection with neural networks and distributed representation of features

We present the problem of selecting relevant premises for a proof of a given statement. When stated as a binary classification task for pairs (conjecture, axiom), it can be efficiently solved using artificial neural networks. The key difference between our advance to solve this problem and previous approaches is the use of just functional signatures of premises. To further improve the performance of the model, we use dimensionality reduction technique, to replace long and sparse signature vectors with their compact and dense embedded versions. These are obtained by firstly defining the concept of a context for each functor symbol, and then training a simple neural network to predict the distribution of other functor symbols in the context of this functor. After training the network, the output of its hidden layer is used to construct a lower dimensional embedding of a functional signature (for each premise) with a distributed representation of features. This allows us to use 512-dimensional embeddings for conjecture-axiom pairs, containing enough information about the original statements to reach the accuracy of 76.45% in premise selection task, only with simple two-layer densely connected neural networks.