Machine Learning for Quantifier Selection in cvc5

In this work we considerably improve the state-of-the-art SMT solving on first-order quantified problems by efficient machine learning guidance of quantifier selection. Quantifiers represent a significant challenge for SMT and are technically a source of undecidability. In our approach, we train an efficient machine learning model that informs the solver which quantifiers should be instantiated and which not. Each quantifier may be instantiated multiple times and the set of the active quantifiers changes as the solving progresses. Therefore, we invoke the ML predictor many times, during the whole run of the solver. To make this efficient, we use fast ML models based on gradient boosting decision trees. We integrate our approach into the state-of-the-art cvc5 SMT solver and show a considerable increase of the system's holdout-set performance after training it on a large set of first-order problems collected from the Mizar Mathematical Library.

Graph2Tac: Learning Hierarchical Representations of Math Concepts in Theorem proving

Concepts abound in mathematics and its applications. They vary greatly between subject areas, and new ones are introduced in each mathematical paper or application. A formal theory builds a hierarchy of definitions, theorems and proofs that reference each other. When an AI agent is proving a new theorem, most of the mathematical concepts and lemmas relevant to that theorem may have never been seen during training. This is especially true in the Coq proof assistant, which has a diverse library of Coq projects, each with its own definitions, lemmas, and even custom tactic procedures used to prove those lemmas. It is essential for agents to incorporate such new information into their knowledge base on the fly. We work towards this goal by utilizing a new, large-scale, graph-based dataset for machine learning in Coq. We leverage a faithful graph-representation of Coq terms that induces a directed graph of dependencies between definitions to create a novel graph neural network, Graph2Tac (G2T), that takes into account not only the current goal, but also the entire hierarchy of definitions that led to the current goal. G2T is an online model that is deeply integrated into the users' workflow and can adapt in real time to new Coq projects and their definitions. It complements well with other online models that learn in real time from new proof scripts. Our novel definition embedding task, which is trained to compute representations of mathematical concepts not seen during training, boosts the performance of the neural network to rival state-of-the-art k-nearest neighbor predictors.

Graph Neural Networks For Mapping Variables Between Programs -- Extended Version

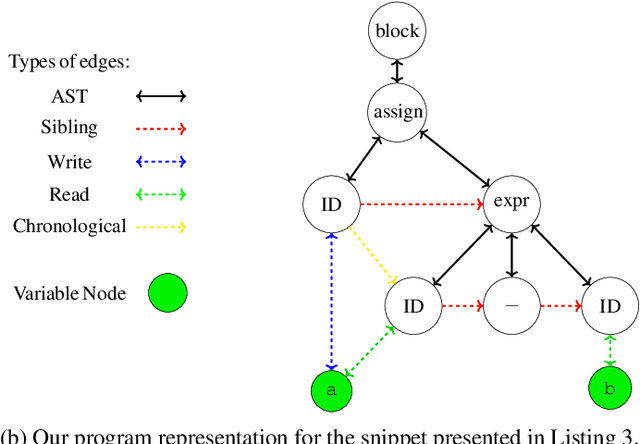
Automated program analysis is a pivotal research domain in many areas of Computer Science -- Formal Methods and Artificial Intelligence, in particular. Due to the undecidability of the problem of program equivalence, comparing two programs is highly challenging. Typically, in order to compare two programs, a relation between both programs' sets of variables is required. Thus, mapping variables between two programs is useful for a panoply of tasks such as program equivalence, program analysis, program repair, and clone detection. In this work, we propose using graph neural networks (GNNs) to map the set of variables between two programs based on both programs' abstract syntax trees (ASTs). To demonstrate the strength of variable mappings, we present three use-cases of these mappings on the task of program repair to fix well-studied and recurrent bugs among novice programmers in introductory programming assignments (IPAs). Experimental results on a dataset of 4166 pairs of incorrect/correct programs show that our approach correctly maps 83% of the evaluation dataset. Moreover, our experiments show that the current state-of-the-art on program repair, greatly dependent on the programs' structure, can only repair about 72% of the incorrect programs. In contrast, our approach, which is solely based on variable mappings, can repair around 88.5%.

Machine Learning Meets The Herbrand Universe

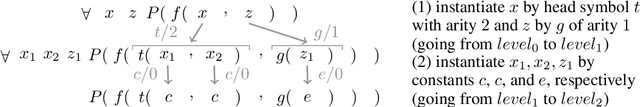
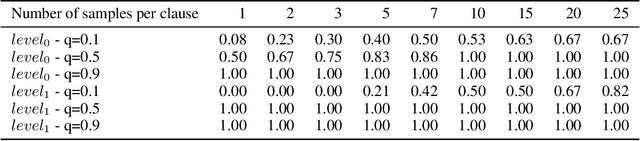
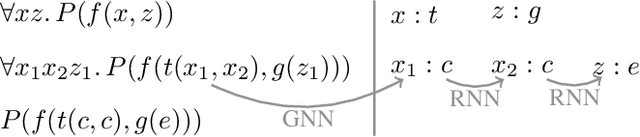
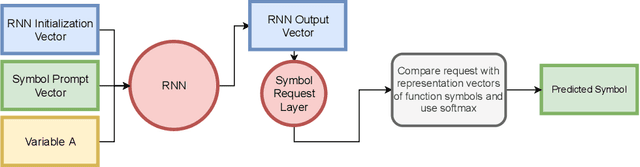
The appearance of strong CDCL-based propositional (SAT) solvers has greatly advanced several areas of automated reasoning (AR). One of the directions in AR is thus to apply SAT solvers to expressive formalisms such as first-order logic, for which large corpora of general mathematical problems exist today. This is possible due to Herbrand's theorem, which allows reduction of first-order problems to propositional problems by instantiation. The core challenge is choosing the right instances from the typically infinite Herbrand universe. In this work, we develop the first machine learning system targeting this task, addressing its combinatorial and invariance properties. In particular, we develop a GNN2RNN architecture based on an invariant graph neural network (GNN) that learns from problems and their solutions independently of symbol names (addressing the abundance of skolems), combined with a recurrent neural network (RNN) that proposes for each clause its instantiations. The architecture is then trained on a corpus of mathematical problems and their instantiation-based proofs, and its performance is evaluated in several ways. We show that the trained system achieves high accuracy in predicting the right instances, and that it is capable of solving many problems by educated guessing when combined with a ground solver. To our knowledge, this is the first convincing use of machine learning in synthesizing relevant elements from arbitrary Herbrand universes.

The Isabelle ENIGMA

We significantly improve the performance of the E automated theorem prover on the Isabelle Sledgehammer problems by combining learning and theorem proving in several ways. In particular, we develop targeted versions of the ENIGMA guidance for the Isabelle problems, targeted versions of neural premise selection, and targeted strategies for E. The methods are trained in several iterations over hundreds of thousands untyped and typed first-order problems extracted from Isabelle. Our final best single-strategy ENIGMA and premise selection system improves the best previous version of E by 25.3% in 15 seconds, outperforming also all other previous ATP and SMT systems.

Learning Equational Theorem Proving

We develop Stratified Shortest Solution Imitation Learning (3SIL) to learn equational theorem proving in a deep reinforcement learning (RL) setting. The self-trained models achieve state-of-the-art performance in proving problems generated by one of the top open conjectures in quasigroup theory, the Abelian Inner Mapping (AIM) Conjecture. To develop the methods, we first use two simpler arithmetic rewriting tasks that share tree-structured proof states and sparse rewards with the AIM problems. On these tasks, 3SIL is shown to significantly outperform several established RL and imitation learning methods. The final system is then evaluated in a standalone and cooperative mode on the AIM problems. The standalone 3SIL-trained system proves in 60 seconds more theorems (70.2%) than the complex, hand-engineered Waldmeister system (65.5%). In the cooperative mode, the final system is combined with the Prover9 system, proving in 2 seconds what standalone Prover9 proves in 60 seconds.