Learning Guided Automated Reasoning: A Brief Survey

Automated theorem provers and formal proof assistants are general reasoning systems that are in theory capable of proving arbitrarily hard theorems, thus solving arbitrary problems reducible to mathematics and logical reasoning. In practice, such systems however face large combinatorial explosion, and therefore include many heuristics and choice points that considerably influence their performance. This is an opportunity for trained machine learning predictors, which can guide the work of such reasoning systems. Conversely, deductive search supported by the notion of logically valid proof allows one to train machine learning systems on large reasoning corpora. Such bodies of proof are usually correct by construction and when combined with more and more precise trained guidance they can be boostrapped into very large corpora, with increasingly long reasoning chains and possibly novel proof ideas. In this paper we provide an overview of several automated reasoning and theorem proving domains and the learning and AI methods that have been so far developed for them. These include premise selection, proof guidance in several settings, AI systems and feedback loops iterating between reasoning and learning, and symbolic classification problems.

Graph2Tac: Learning Hierarchical Representations of Math Concepts in Theorem proving

Concepts abound in mathematics and its applications. They vary greatly between subject areas, and new ones are introduced in each mathematical paper or application. A formal theory builds a hierarchy of definitions, theorems and proofs that reference each other. When an AI agent is proving a new theorem, most of the mathematical concepts and lemmas relevant to that theorem may have never been seen during training. This is especially true in the Coq proof assistant, which has a diverse library of Coq projects, each with its own definitions, lemmas, and even custom tactic procedures used to prove those lemmas. It is essential for agents to incorporate such new information into their knowledge base on the fly. We work towards this goal by utilizing a new, large-scale, graph-based dataset for machine learning in Coq. We leverage a faithful graph-representation of Coq terms that induces a directed graph of dependencies between definitions to create a novel graph neural network, Graph2Tac (G2T), that takes into account not only the current goal, but also the entire hierarchy of definitions that led to the current goal. G2T is an online model that is deeply integrated into the users' workflow and can adapt in real time to new Coq projects and their definitions. It complements well with other online models that learn in real time from new proof scripts. Our novel definition embedding task, which is trained to compute representations of mathematical concepts not seen during training, boosts the performance of the neural network to rival state-of-the-art k-nearest neighbor predictors.

The Tactician's Web of Large-Scale Formal Knowledge

The Tactician's Web is a platform offering a large web of strongly interconnected, machine-checked, formal mathematical knowledge conveniently packaged for machine learning, analytics, and proof engineering. Built on top of the Coq proof assistant, the platform exports a dataset containing a wide variety of formal theories, presented as a web of definitions, theorems, proof terms, tactics, and proof states. Theories are encoded both as a semantic graph (rendered below) and as human-readable text, each with a unique set of advantages and disadvantages. Proving agents may interact with Coq through the same rich data representation and can be automatically benchmarked on a set of theorems. Tight integration with Coq provides the unique possibility to make agents available to proof engineers as practical tools.

Online Machine Learning Techniques for Coq: A Comparison

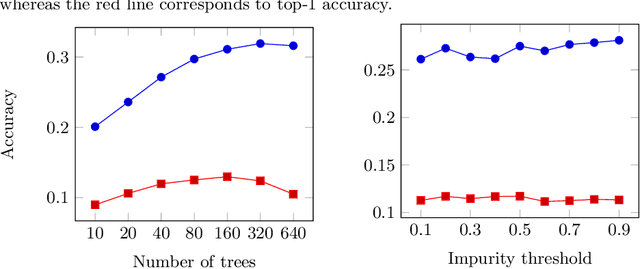
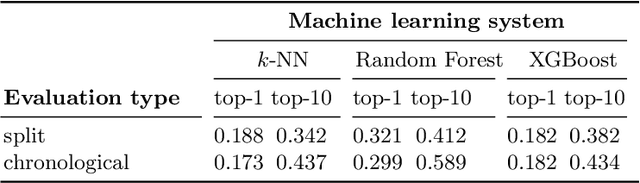
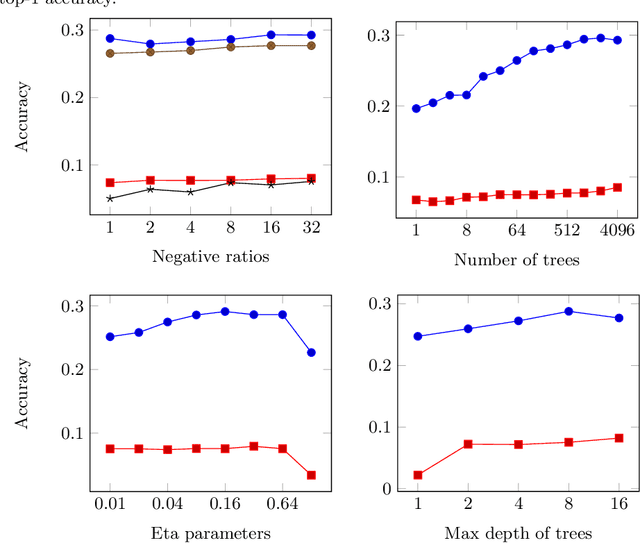
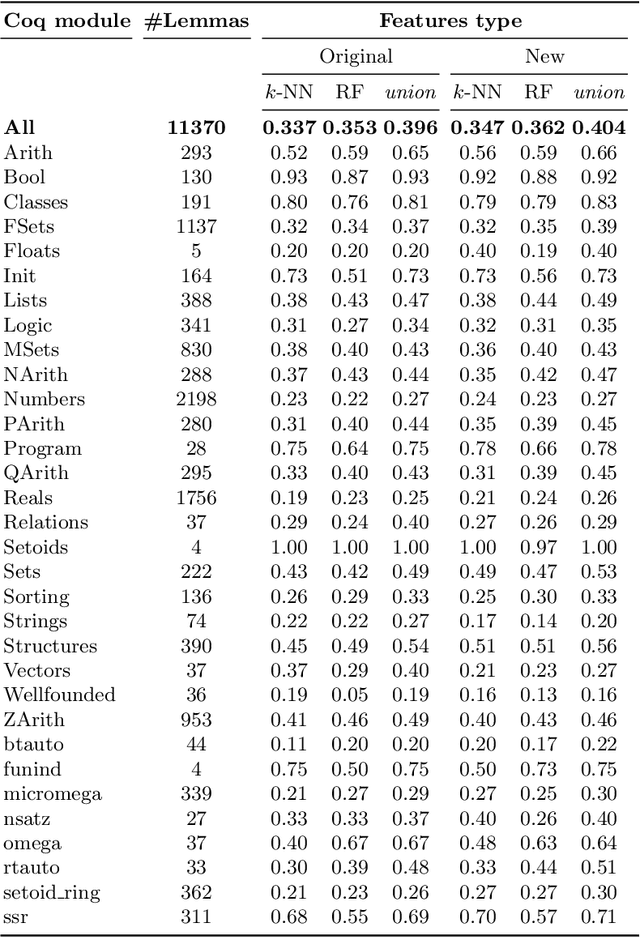
We present a comparison of several online machine learning techniques for tactical learning and proving in the Coq proof assistant. This work builds on top of Tactician, a plugin for Coq that learns from proofs written by the user to synthesize new proofs. This learning happens in an online manner -- meaning that Tactician's machine learning model is updated immediately every time the user performs a step in an interactive proof. This has important advantages compared to the more studied offline learning systems: (1) it provides the user with a seamless, interactive experience with Tactician and, (2) it takes advantage of locality of proof similarity, which means that proofs similar to the current proof are likely to be found close by. We implement two online methods, namely approximate $k$-nearest neighbors based on locality sensitive hashing forests and random decision forests. Additionally, we conduct experiments with gradient boosted trees in an offline setting using XGBoost. We compare the relative performance of Tactician using these three learning methods on Coq's standard library.

The Tactician (extended version): A Seamless, Interactive Tactic Learner and Prover for Coq

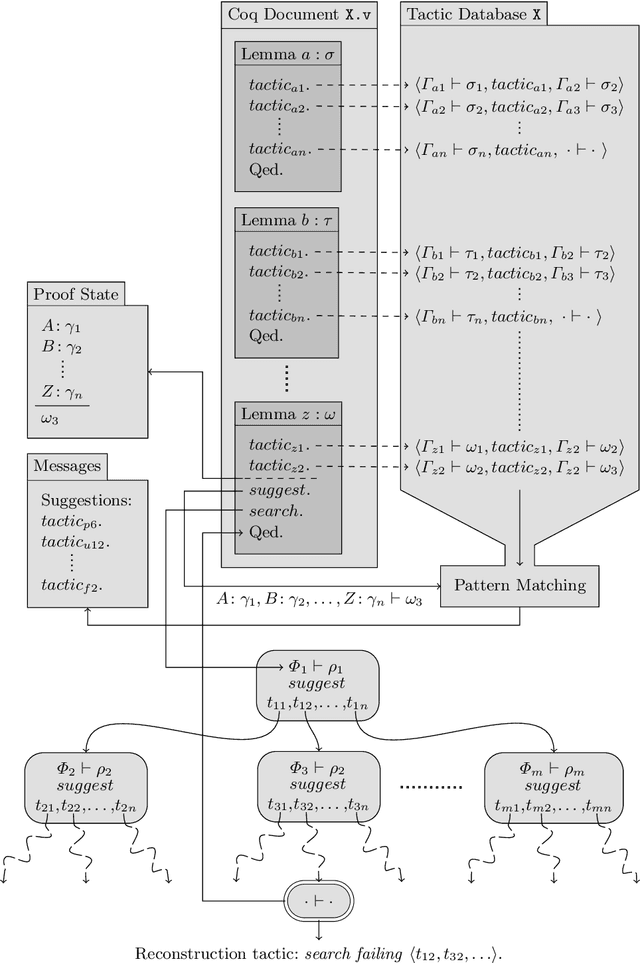
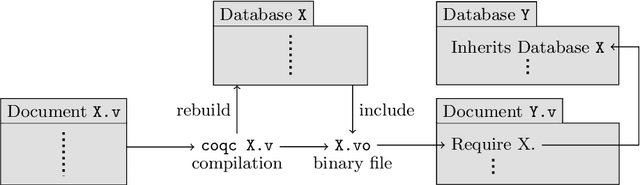
We present Tactician, a tactic learner and prover for the Coq Proof Assistant. Tactician helps users make tactical proof decisions while they retain control over the general proof strategy. To this end, Tactician learns from previously written tactic scripts and gives users either suggestions about the next tactic to be executed or altogether takes over the burden of proof synthesis. Tactician's goal is to provide users with a seamless, interactive, and intuitive experience together with robust and adaptive proof automation. In this paper, we give an overview of Tactician from the user's point of view, regarding both day-to-day usage and issues of package dependency management while learning in the large. Finally, we give a peek into Tactician's implementation as a Coq plugin and machine learning platform.

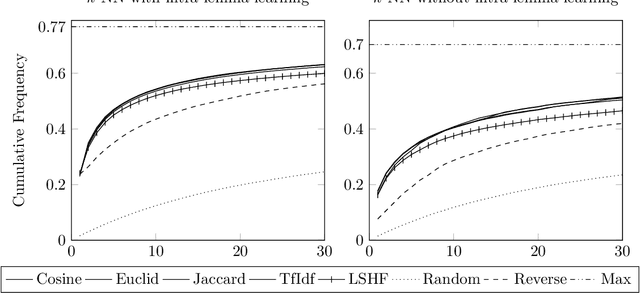
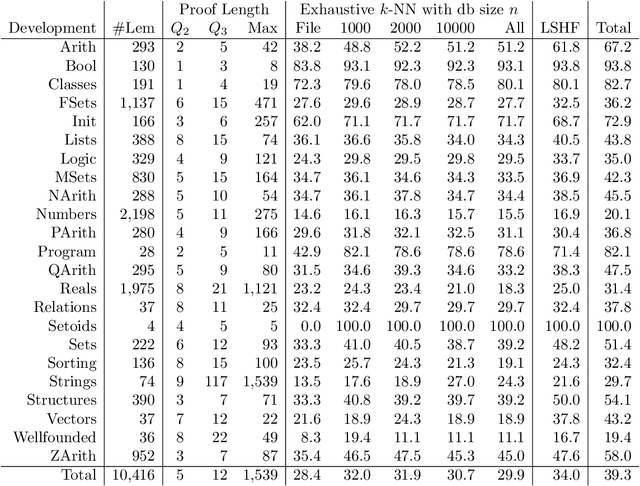
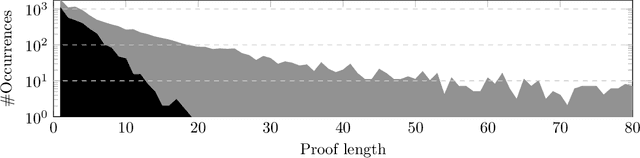
Tactic Learning and Proving for the Coq Proof Assistant

We present a system that utilizes machine learning for tactic proof search in the Coq Proof Assistant. In a similar vein as the TacticToe project for HOL4, our system predicts appropriate tactics and finds proofs in the form of tactic scripts. To do this, it learns from previous tactic scripts and how they are applied to proof states. The performance of the system is evaluated on the Coq Standard Library. Currently, our predictor can identify the correct tactic to be applied to a proof state 23.4% of the time. Our proof searcher can fully automatically prove 39.3% of the lemmas. When combined with the CoqHammer system, the two systems together prove 56.7% of the library's lemmas.