Regularization in Spider-Style Strategy Discovery and Schedule Construction

To achieve the best performance, automatic theorem provers often rely on schedules of diverse proving strategies to be tried out (either sequentially or in parallel) on a given problem. In this paper, we report on a large-scale experiment with discovering strategies for the Vampire prover, targeting the FOF fragment of the TPTP library and constructing a schedule for it, based on the ideas of Andrei Voronkov's system Spider. We examine the process from various angles, discuss the difficulty (or ease) of obtaining a strong Vampire schedule for the CASC competition, and establish how well a schedule can be expected to generalize to unseen problems and what factors influence this property.

Learning Guided Automated Reasoning: A Brief Survey

Automated theorem provers and formal proof assistants are general reasoning systems that are in theory capable of proving arbitrarily hard theorems, thus solving arbitrary problems reducible to mathematics and logical reasoning. In practice, such systems however face large combinatorial explosion, and therefore include many heuristics and choice points that considerably influence their performance. This is an opportunity for trained machine learning predictors, which can guide the work of such reasoning systems. Conversely, deductive search supported by the notion of logically valid proof allows one to train machine learning systems on large reasoning corpora. Such bodies of proof are usually correct by construction and when combined with more and more precise trained guidance they can be boostrapped into very large corpora, with increasingly long reasoning chains and possibly novel proof ideas. In this paper we provide an overview of several automated reasoning and theorem proving domains and the learning and AI methods that have been so far developed for them. These include premise selection, proof guidance in several settings, AI systems and feedback loops iterating between reasoning and learning, and symbolic classification problems.

Learning Planning Action Models from State Traces

Previous STRIPS domain model acquisition approaches that learn from state traces start with the names and parameters of the actions to be learned. Therefore their only task is to deduce the preconditions and effects of the given actions. In this work, we explore learning in situations when the parameters of learned actions are not provided. We define two levels of trace quality based on which information is provided and present an algorithm for each. In one level (L1), the states in the traces are labeled with action names, so we can deduce the number and names of the actions, but we still need to work out the number and types of parameters. In the other level (L2), the states are additionally labeled with objects that constitute the parameters of the corresponding grounded actions. Here we still need to deduce the types of the parameters in the learned actions. We experimentally evaluate the proposed algorithms and compare them with the state-of-the-art learning tool FAMA on a large collection of IPC benchmarks. The evaluation shows that our new algorithms are faster, can handle larger inputs and provide better results in terms of learning action models more similar to reference models.

MizAR 60 for Mizar 50

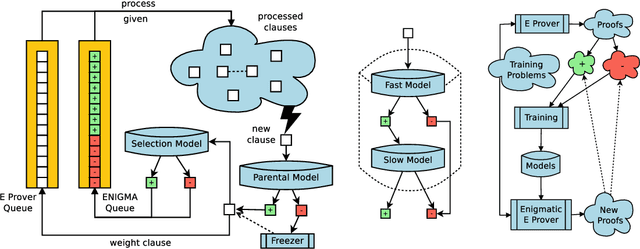
As a present to Mizar on its 50th anniversary, we develop an AI/TP system that automatically proves about 60\% of the Mizar theorems in the hammer setting. We also automatically prove 75\% of the Mizar theorems when the automated provers are helped by using only the premises used in the human-written Mizar proofs. We describe the methods and large-scale experiments leading to these results. This includes in particular the E and Vampire provers, their ENIGMA and Deepire learning modifications, a number of learning-based premise selection methods, and the incremental loop that interleaves growing a corpus of millions of ATP proofs with training increasingly strong AI/TP systems on them. We also present a selection of Mizar problems that were proved automatically.

New Techniques that Improve ENIGMA-style Clause Selection Guidance

We re-examine the topic of machine-learned clause selection guidance in saturation-based theorem provers. The central idea, recently popularized by the ENIGMA system, is to learn a classifier for recognizing clauses that appeared in previously discovered proofs. In subsequent runs, clauses classified positively are prioritized for selection. We propose several improvements to this approach and experimentally confirm their viability. For the demonstration, we use a Recursive Neural Network to classify clauses based on their derivation history and the presence or absence of automatically supplied theory axioms therein. The automatic theorem prover Vampire guided by the network achieves a 41% improvement on a relevant subset of SMT-LIB in a real time evaluation.

Vampire With a Brain Is a Good ITP Hammer

Vampire has been for a long time the strongest first-order automated theorem prover, widely used for hammer-style proof automation in ITPs such as Mizar, Isabelle, HOL and Coq. In this work, we considerably improve the performance of Vampire in hammering over the full Mizar library by enhancing its saturation procedure with efficient neural guidance. In particular, we employ a recursive neural network classifying the generated clauses based only on their derivation history. Compared to previous neural methods based on considering the logical content of the clauses, this leads to large real-time speedup of the neural guidance. The resulting system shows good learning capability and achieves state-of-the-art performance on the Mizar library, while proving many theorems that the related ENIGMA system could not prove in a similar hammering evaluation.

ENIGMA Anonymous: Symbol-Independent Inference Guiding Machine (system description)

We describe an implementation of gradient boosting and neural guidance of saturation-style automated theorem provers that does not depend on consistent symbol names across problems. For the gradient-boosting guidance, we manually create abstracted features by considering arity-based encodings of formulas. For the neural guidance, we use symbol-independent graph neural networks and their embedding of the terms and clauses. The two methods are efficiently implemented in the E prover and its ENIGMA learning-guided framework and evaluated on the MPTP large-theory benchmark. Both methods are shown to achieve comparable real-time performance to state-of-the-art symbol-based methods.

ENIGMA-NG: Efficient Neural and Gradient-Boosted Inference Guidance for E

We describe an efficient implementation of clause guidance in saturation-based automated theorem provers extending the ENIGMA approach. Unlike in the first ENIGMA implementation where fast linear classifier is trained and used together with manually engineered features, we have started to experiment with more sophisticated state-of-the-art machine learning methods such as gradient boosted trees and recursive neural networks. In particular the latter approach poses challenges in terms of efficiency of clause evaluation, however, we show that deep integration of the neural evaluation with the ATP data-structures can largely amortize this cost and lead to competitive real-time results. Both methods are evaluated on a large dataset of theorem proving problems and compared with the previous approaches. The resulting methods improve on the manually designed clause guidance, providing the first practically convincing application of gradient-boosted and neural clause guidance in saturation-style automated theorem provers.

Selecting the Selection

Modern saturation-based Automated Theorem Provers typically implement the superposition calculus for reasoning about first-order logic with or without equality. Practical implementations of this calculus use a variety of literal selections and term orderings to tame the growth of the search space and help steer proof search. This paper introduces the notion of lookahead selection that estimates (looks ahead) the effect on the search space of selecting a literal. There is also a case made for the use of incomplete selection functions that attempt to restrict the search space instead of satisfying some completeness criteria. Experimental evaluation in the \Vampire\ theorem prover shows that both lookahead selection and incomplete selection significantly contribute to solving hard problems unsolvable by other methods.

Duality in STRIPS planning

We describe a duality mapping between STRIPS planning tasks. By exchanging the initial and goal conditions, taking their respective complements, and swapping for every action its precondition and delete list, one obtains for every STRIPS task its dual version, which has a solution if and only if the original does. This is proved by showing that the described transformation essentially turns progression (forward search) into regression (backward search) and vice versa. The duality sheds new light on STRIPS planning by allowing a transfer of ideas from one search approach to the other. It can be used to construct new algorithms from old ones, or (equivalently) to obtain new benchmarks from existing ones. Experiments show that the dual versions of IPC benchmarks are in general quite difficult for modern planners. This may be seen as a new challenge. On the other hand, the cases where the dual versions are easier to solve demonstrate that the duality can also be made useful in practice.