Machine Learning for Quantifier Selection in cvc5

In this work we considerably improve the state-of-the-art SMT solving on first-order quantified problems by efficient machine learning guidance of quantifier selection. Quantifiers represent a significant challenge for SMT and are technically a source of undecidability. In our approach, we train an efficient machine learning model that informs the solver which quantifiers should be instantiated and which not. Each quantifier may be instantiated multiple times and the set of the active quantifiers changes as the solving progresses. Therefore, we invoke the ML predictor many times, during the whole run of the solver. To make this efficient, we use fast ML models based on gradient boosting decision trees. We integrate our approach into the state-of-the-art cvc5 SMT solver and show a considerable increase of the system's holdout-set performance after training it on a large set of first-order problems collected from the Mizar Mathematical Library.

Solving Hard Mizar Problems with Instantiation and Strategy Invention

In this work, we prove over 3000 previously ATP-unproved Mizar/MPTP problems by using several ATP and AI methods, raising the number of ATP-solved Mizar problems from 75\% to above 80\%. First, we start to experiment with the cvc5 SMT solver which uses several instantiation-based heuristics that differ from the superposition-based systems, that were previously applied to Mizar,and add many new solutions. Then we use automated strategy invention to develop cvc5 strategies that largely improve cvc5's performance on the hard problems. In particular, the best invented strategy solves over 14\% more problems than the best previously available cvc5 strategy. We also show that different clausification methods have a high impact on such instantiation-based methods, again producing many new solutions. In total, the methods solve 3021 (21.3\%) of the 14163 previously unsolved hard Mizar problems. This is a new milestone over the Mizar large-theory benchmark and a large strengthening of the hammer methods for Mizar.

Learning Guided Automated Reasoning: A Brief Survey

Automated theorem provers and formal proof assistants are general reasoning systems that are in theory capable of proving arbitrarily hard theorems, thus solving arbitrary problems reducible to mathematics and logical reasoning. In practice, such systems however face large combinatorial explosion, and therefore include many heuristics and choice points that considerably influence their performance. This is an opportunity for trained machine learning predictors, which can guide the work of such reasoning systems. Conversely, deductive search supported by the notion of logically valid proof allows one to train machine learning systems on large reasoning corpora. Such bodies of proof are usually correct by construction and when combined with more and more precise trained guidance they can be boostrapped into very large corpora, with increasingly long reasoning chains and possibly novel proof ideas. In this paper we provide an overview of several automated reasoning and theorem proving domains and the learning and AI methods that have been so far developed for them. These include premise selection, proof guidance in several settings, AI systems and feedback loops iterating between reasoning and learning, and symbolic classification problems.

MizAR 60 for Mizar 50

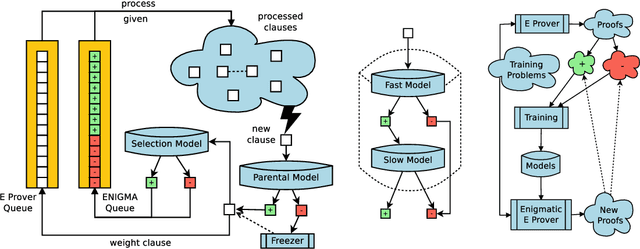
As a present to Mizar on its 50th anniversary, we develop an AI/TP system that automatically proves about 60\% of the Mizar theorems in the hammer setting. We also automatically prove 75\% of the Mizar theorems when the automated provers are helped by using only the premises used in the human-written Mizar proofs. We describe the methods and large-scale experiments leading to these results. This includes in particular the E and Vampire provers, their ENIGMA and Deepire learning modifications, a number of learning-based premise selection methods, and the incremental loop that interleaves growing a corpus of millions of ATP proofs with training increasingly strong AI/TP systems on them. We also present a selection of Mizar problems that were proved automatically.

The Isabelle ENIGMA

We significantly improve the performance of the E automated theorem prover on the Isabelle Sledgehammer problems by combining learning and theorem proving in several ways. In particular, we develop targeted versions of the ENIGMA guidance for the Isabelle problems, targeted versions of neural premise selection, and targeted strategies for E. The methods are trained in several iterations over hundreds of thousands untyped and typed first-order problems extracted from Isabelle. Our final best single-strategy ENIGMA and premise selection system improves the best previous version of E by 25.3% in 15 seconds, outperforming also all other previous ATP and SMT systems.

Learning Theorem Proving Components

Saturation-style automated theorem provers (ATPs) based on the given clause procedure are today the strongest general reasoners for classical first-order logic. The clause selection heuristics in such systems are, however, often evaluating clauses in isolation, ignoring other clauses. This has changed recently by equipping the E/ENIGMA system with a graph neural network (GNN) that chooses the next given clause based on its evaluation in the context of previously selected clauses. In this work, we describe several algorithms and experiments with ENIGMA, advancing the idea of contextual evaluation based on learning important components of the graph of clauses.

Fast and Slow Enigmas and Parental Guidance

We describe several additions to the ENIGMA system that guides clause selection in the E automated theorem prover. First, we significantly speed up its neural guidance by adding server-based GPU evaluation. The second addition is motivated by fast weight-based rejection filters that are currently used in systems like E and Prover9. Such systems can be made more intelligent by instead training fast versions of ENIGMA that implement more intelligent pre-filtering. This results in combinations of trainable fast and slow thinking that improves over both the fast-only and slow-only methods. The third addition is based on "judging the children by their parents", i.e., possibly rejecting an inference before it produces a clause. This is motivated by standard evolutionary mechanisms, where there is always a cost to producing all possible offsprings in the current population. This saves time by not evaluating all clauses by more expensive methods and provides a complementary view of the generated clauses. The methods are evaluated on a large benchmark coming from the Mizar Mathematical Library, showing good improvements over the state of the art.

First Neural Conjecturing Datasets and Experiments

We describe several datasets and first experiments with creating conjectures by neural methods. The datasets are based on the Mizar Mathematical Library processed in several forms and the problems extracted from it by the MPTP system and proved by the E prover using the ENIGMA guidance. The conjecturing experiments use the Transformer architecture and in particular its GPT-2 implementation.

ENIGMA Anonymous: Symbol-Independent Inference Guiding Machine (system description)

We describe an implementation of gradient boosting and neural guidance of saturation-style automated theorem provers that does not depend on consistent symbol names across problems. For the gradient-boosting guidance, we manually create abstracted features by considering arity-based encodings of formulas. For the neural guidance, we use symbol-independent graph neural networks and their embedding of the terms and clauses. The two methods are efficiently implemented in the E prover and its ENIGMA learning-guided framework and evaluated on the MPTP large-theory benchmark. Both methods are shown to achieve comparable real-time performance to state-of-the-art symbol-based methods.

ENIGMAWatch: ProofWatch Meets ENIGMA

In this work we describe a new learning-based proof guidance -- ENIGMAWatch -- for saturation-style first-order theorem provers. ENIGMAWatch combines two guiding approaches for the given-clause selection implemented for the E ATP system: ProofWatch and ENIGMA. ProofWatch is motivated by the watchlist (hints) method and based on symbolic matching of multiple related proofs, while ENIGMA is based on statistical machine learning. The two methods are combined by using the evolving information about symbolic proof matching as an additional information that characterizes the saturation-style proof search for the statistical learning methods. The new system is experimentally evaluated on a large set of problems from the Mizar Library. We show that the added proof-matching information is considered important by the statistical machine learners, and that it leads to improvements in E's Performance over ProofWatch and ENIGMA.