Learning Conjecturing from Scratch

We develop a self-learning approach for conjecturing of induction predicates on a dataset of 16197 problems derived from the OEIS. These problems are hard for today's SMT and ATP systems because they require a combination of inductive and arithmetical reasoning. Starting from scratch, our approach consists of a feedback loop that iterates between (i) training a neural translator to learn the correspondence between the problems solved so far and the induction predicates useful for them, (ii) using the trained neural system to generate many new induction predicates for the problems, (iii) fast runs of the z3 prover attempting to prove the problems using the generated predicates, (iv) using heuristics such as predicate size and solution speed on the proved problems to choose the best predicates for the next iteration of training. The algorithm discovers on its own many interesting induction predicates, ultimately solving 5565 problems, compared to 2265 problems solved by CVC5, Vampire or Z3 in 60 seconds.

Learning Guided Automated Reasoning: A Brief Survey

Automated theorem provers and formal proof assistants are general reasoning systems that are in theory capable of proving arbitrarily hard theorems, thus solving arbitrary problems reducible to mathematics and logical reasoning. In practice, such systems however face large combinatorial explosion, and therefore include many heuristics and choice points that considerably influence their performance. This is an opportunity for trained machine learning predictors, which can guide the work of such reasoning systems. Conversely, deductive search supported by the notion of logically valid proof allows one to train machine learning systems on large reasoning corpora. Such bodies of proof are usually correct by construction and when combined with more and more precise trained guidance they can be boostrapped into very large corpora, with increasingly long reasoning chains and possibly novel proof ideas. In this paper we provide an overview of several automated reasoning and theorem proving domains and the learning and AI methods that have been so far developed for them. These include premise selection, proof guidance in several settings, AI systems and feedback loops iterating between reasoning and learning, and symbolic classification problems.

Alien Coding

We introduce a self-learning algorithm for synthesizing programs for OEIS sequences. The algorithm starts from scratch initially generating programs at random. Then it runs many iterations of a self-learning loop that interleaves (i) training neural machine translation to learn the correspondence between sequences and the programs discovered so far, and (ii) proposing many new programs for each OEIS sequence by the trained neural machine translator. The algorithm discovers on its own programs for more than 78000 OEIS sequences, sometimes developing unusual programming methods. We analyze its behavior and the invented programs in several experiments.

Program Synthesis for the OEIS

We present a self-learning approach to synthesize programs for integer sequences. Our method relies on a tree search equipped with a semantic quotient guided by a learned policy. Through self-learning, our implementation discovers in one week programs that generate the first 16 numbers of 43516 OEIS sequences with sequences identical up to the 16th number counted only once.

Tree Neural Networks in HOL4

We present an implementation of tree neural networks within the proof assistant HOL4. Their architecture makes them naturally suited for approximating functions whose domain is a set of formulas. We measure the performance of our implementation and compare it with other machine learning predictors on the tasks of evaluating arithmetical expressions and estimating the truth of propositional formulas.

Self-Learned Formula Synthesis in Set Theory

A reinforcement learning algorithm accomplishes the task of synthesizing a set-theoretical formula that evaluates to given truth values for given assignments.

Deep Reinforcement Learning in HOL4

The paper describes an implementation of deep reinforcement learning through self-supervised learning within the proof assistant HOL4. A close interaction between the machine learning modules and the HOL4 library is achieved by the choice of tree neural networks (TNNs) as machine learning models and the internal use of HOL4 terms to represent tree structures of TNNs. Recursive improvement is possible when a given task is expressed as a search problem. In this case, a Monte Carlo Tree Search (MCTS) algorithm guided by a TNN can be used to explore the search space and produce better examples for training the next TNN. As an illustration, tasks over propositional and arithmetical terms, representative of fundamental theorem proving techniques, are specified and learned: truth estimation, end-to-end computation, term rewriting and term synthesis.

Learning to Prove with Tactics

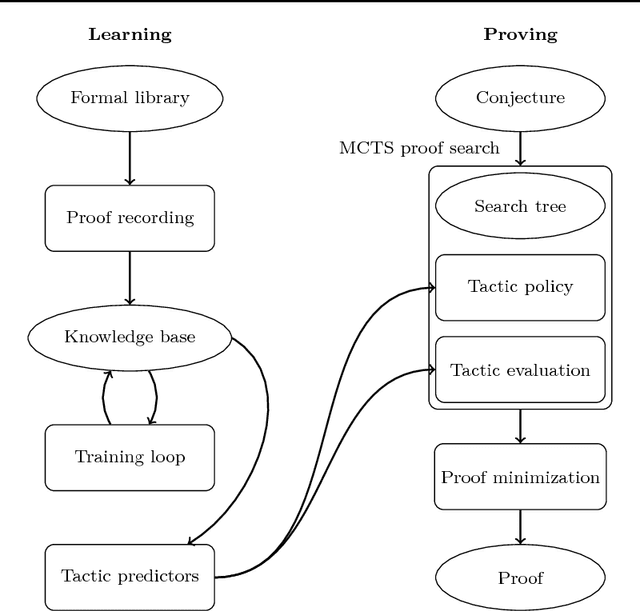
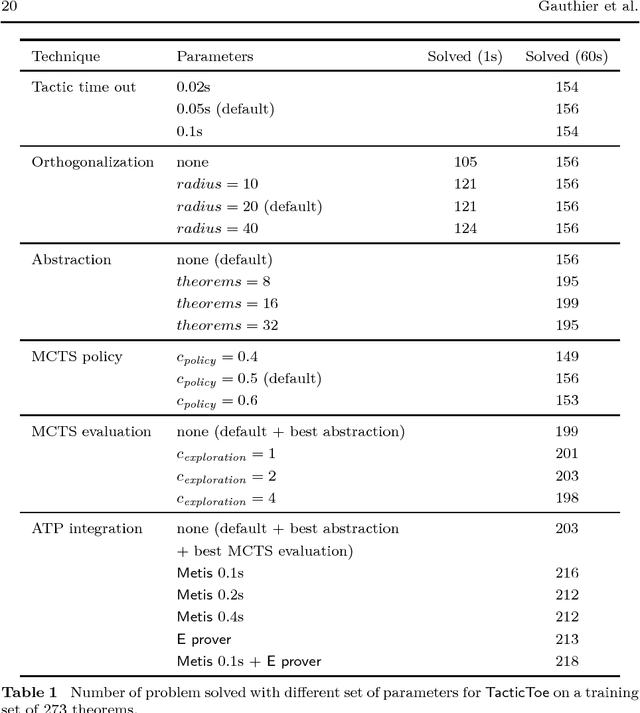
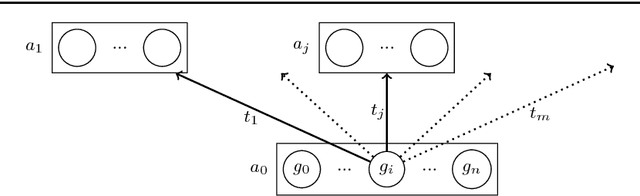
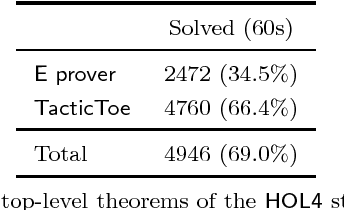
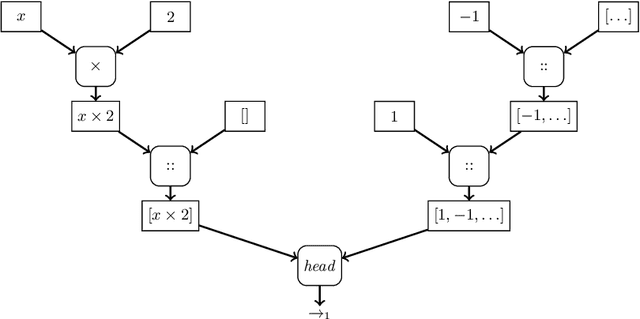
We implement a automated tactical prover TacticToe on top of the HOL4 interactive theorem prover. TacticToe learns from human proofs which mathematical technique is suitable in each proof situation. This knowledge is then used in a Monte Carlo tree search algorithm to explore promising tactic-level proof paths. On a single CPU, with a time limit of 60 seconds, TacticToe proves 66.4 percent of the 7164 theorems in HOL4's standard library, whereas E prover with auto-schedule solves 34.5 percent. The success rate rises to 69.0 percent by combining the results of TacticToe and E prover.

Learning to Reason with HOL4 tactics

Techniques combining machine learning with translation to automated reasoning have recently become an important component of formal proof assistants. Such "hammer" tech- niques complement traditional proof assistant automation as implemented by tactics and decision procedures. In this paper we present a unified proof assistant automation approach which attempts to automate the selection of appropriate tactics and tactic-sequences com- bined with an optimized small-scale hammering approach. We implement the technique as a tactic-level automation for HOL4: TacticToe. It implements a modified A*-algorithm directly in HOL4 that explores different tactic-level proof paths, guiding their selection by learning from a large number of previous tactic-level proofs. Unlike the existing hammer methods, TacticToe avoids translation to FOL, working directly on the HOL level. By combining tactic prediction and premise selection, TacticToe is able to re-prove 39 percent of 7902 HOL4 theorems in 5 seconds whereas the best single HOL(y)Hammer strategy solves 32 percent in the same amount of time.

Premise Selection and External Provers for HOL4

Learning-assisted automated reasoning has recently gained popularity among the users of Isabelle/HOL, HOL Light, and Mizar. In this paper, we present an add-on to the HOL4 proof assistant and an adaptation of the HOLyHammer system that provides machine learning-based premise selection and automated reasoning also for HOL4. We efficiently record the HOL4 dependencies and extract features from the theorem statements, which form a basis for premise selection. HOLyHammer transforms the HOL4 statements in the various TPTP-ATP proof formats, which are then processed by the ATPs. We discuss the different evaluation settings: ATPs, accessible lemmas, and premise numbers. We measure the performance of HOLyHammer on the HOL4 standard library. The results are combined accordingly and compared with the HOL Light experiments, showing a comparably high quality of predictions. The system directly benefits HOL4 users by automatically finding proofs dependencies that can be reconstructed by Metis.