Automated Strategy Invention for Confluence of Term Rewrite Systems

Term rewriting plays a crucial role in software verification and compiler optimization. With dozens of highly parameterizable techniques developed to prove various system properties, automatic term rewriting tools work in an extensive parameter space. This complexity exceeds human capacity for parameter selection, motivating an investigation into automated strategy invention. In this paper, we focus on confluence, an important property of term rewrite systems, and apply machine learning to develop the first learning-guided automatic confluence prover. Moreover, we randomly generate a large dataset to analyze confluence for term rewrite systems. Our results focus on improving the state-of-the-art automatic confluence prover CSI: When equipped with our invented strategies, it surpasses its human-designed strategies both on the augmented dataset and on the original human-created benchmark dataset Cops, proving/disproving the confluence of several term rewrite systems for which no automated proofs were known before.

Learning Rules Explaining Interactive Theorem Proving Tactic Prediction

Formally verifying the correctness of mathematical proofs is more accessible than ever, however, the learning curve remains steep for many of the state-of-the-art interactive theorem provers (ITP). Deriving the most appropriate subsequent proof step, and reasoning about it, given the multitude of possibilities, remains a daunting task for novice users. To improve the situation, several investigations have developed machine learning based guidance for tactic selection. Such approaches struggle to learn non-trivial relationships between the chosen tactic and the structure of the proof state and represent them as symbolic expressions. To address these issues we (i) We represent the problem as an Inductive Logic Programming (ILP) task, (ii) Using the ILP representation we enriched the feature space by encoding additional, computationally expensive properties as background knowledge predicates, (iii) We use this enriched feature space to learn rules explaining when a tactic is applicable to a given proof state, (iv) we use the learned rules to filter the output of an existing tactic selection approach and empirically show improvement over the non-filtering approaches.

Experiments with Choice in Dependently-Typed Higher-Order Logic

Recently an extension to higher-order logic -- called DHOL -- was introduced, enriching the language with dependent types, and creating a powerful extensional type theory. In this paper we propose two ways how choice can be added to DHOL. We extend the DHOL term structure by Hilbert's indefinite choice operator $\epsilon$, define a translation of the choice terms to HOL choice that extends the existing translation from DHOL to HOL and show that the extension of the translation is complete and give an argument for soundness. We finally evaluate the extended translation on a set of dependent HOL problems that require choice.

Learning Guided Automated Reasoning: A Brief Survey

Automated theorem provers and formal proof assistants are general reasoning systems that are in theory capable of proving arbitrarily hard theorems, thus solving arbitrary problems reducible to mathematics and logical reasoning. In practice, such systems however face large combinatorial explosion, and therefore include many heuristics and choice points that considerably influence their performance. This is an opportunity for trained machine learning predictors, which can guide the work of such reasoning systems. Conversely, deductive search supported by the notion of logically valid proof allows one to train machine learning systems on large reasoning corpora. Such bodies of proof are usually correct by construction and when combined with more and more precise trained guidance they can be boostrapped into very large corpora, with increasingly long reasoning chains and possibly novel proof ideas. In this paper we provide an overview of several automated reasoning and theorem proving domains and the learning and AI methods that have been so far developed for them. These include premise selection, proof guidance in several settings, AI systems and feedback loops iterating between reasoning and learning, and symbolic classification problems.

MizAR 60 for Mizar 50

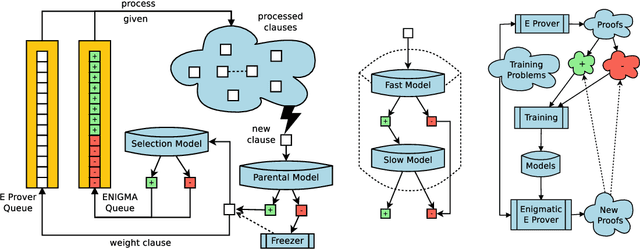
As a present to Mizar on its 50th anniversary, we develop an AI/TP system that automatically proves about 60\% of the Mizar theorems in the hammer setting. We also automatically prove 75\% of the Mizar theorems when the automated provers are helped by using only the premises used in the human-written Mizar proofs. We describe the methods and large-scale experiments leading to these results. This includes in particular the E and Vampire provers, their ENIGMA and Deepire learning modifications, a number of learning-based premise selection methods, and the incremental loop that interleaves growing a corpus of millions of ATP proofs with training increasingly strong AI/TP systems on them. We also present a selection of Mizar problems that were proved automatically.

Differentiable Inductive Logic Programming in High-Dimensional Space

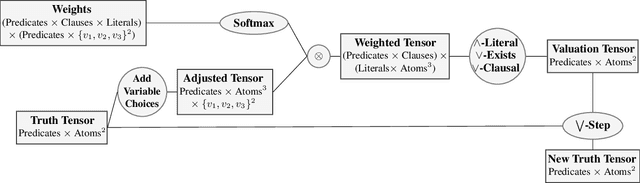
Synthesizing large logic programs through Inductive Logic Programming (ILP) typically requires intermediate definitions. However, cluttering the hypothesis space with intensional predicates often degrades performance. In contrast, gradient descent provides an efficient way to find solutions within such high-dimensional spaces. Neuro-symbolic ILP approaches have not fully exploited this so far. We propose an approach to ILP-based synthesis benefiting from large-scale predicate invention exploiting the efficacy of high-dimensional gradient descent. We find symbolic solutions containing upwards of ten auxiliary definitions. This is beyond the achievements of existing neuro-symbolic ILP systems, thus constituting a milestone in the field.

The Isabelle ENIGMA

We significantly improve the performance of the E automated theorem prover on the Isabelle Sledgehammer problems by combining learning and theorem proving in several ways. In particular, we develop targeted versions of the ENIGMA guidance for the Isabelle problems, targeted versions of neural premise selection, and targeted strategies for E. The methods are trained in several iterations over hundreds of thousands untyped and typed first-order problems extracted from Isabelle. Our final best single-strategy ENIGMA and premise selection system improves the best previous version of E by 25.3% in 15 seconds, outperforming also all other previous ATP and SMT systems.

Adversarial Learning to Reason in an Arbitrary Logic

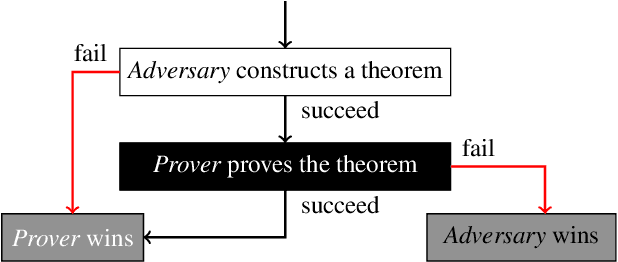
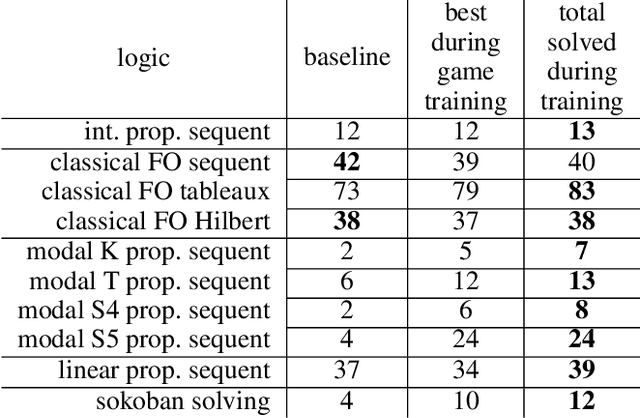
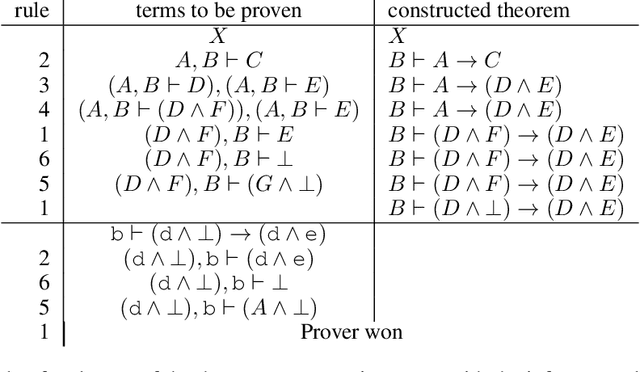
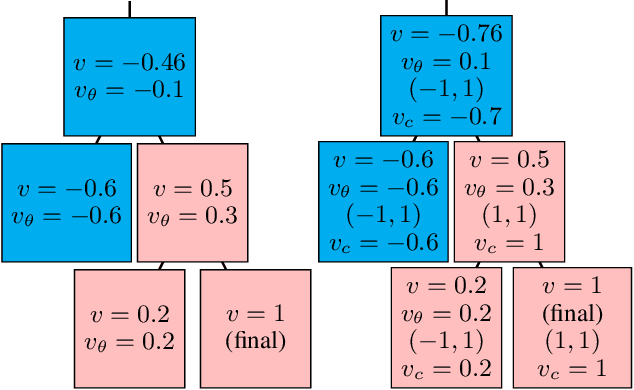
Existing approaches to learning to prove theorems focus on particular logics and datasets. In this work, we propose Monte-Carlo simulations guided by reinforcement learning that can work in an arbitrarily specified logic, without any human knowledge or set of problems. Since the algorithm does not need any training dataset, it is able to learn to work with any logical foundation, even when there is no body of proofs or even conjectures available. We practically demonstrate the feasibility of the approach in multiple logical systems. The approach is stronger than training on randomly generated data but weaker than the approaches trained on tailored axiom and conjecture sets. It however allows us to apply machine learning to automated theorem proving for many logics, where no such attempts have been tried to date, such as intuitionistic logic or linear logic.

Learning Higher-Order Programs without Meta-Interpretive Learning

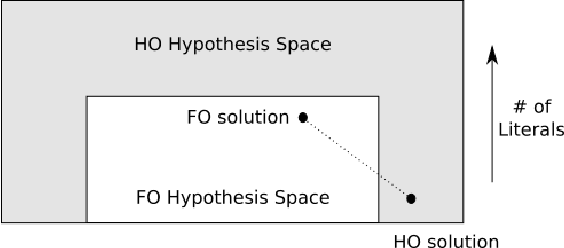
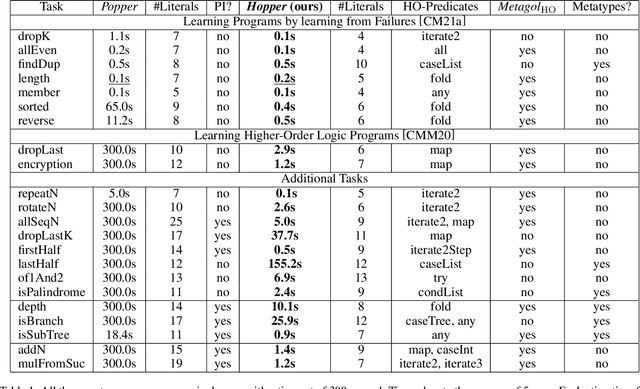
Learning complex programs through inductive logic programming (ILP) remains a formidable challenge. Existing higher-order enabled ILP systems show improved accuracy and learning performance, though remain hampered by the limitations of the underlying learning mechanism. Experimental results show that our extension of the versatile Learning From Failures paradigm by higher-order definitions significantly improves learning performance without the burdensome human guidance required by existing systems. Our theoretical framework captures a class of higher-order definitions preserving soundness of existing subsumption-based pruning methods.

JEFL: Joint Embedding of Formal Proof Libraries

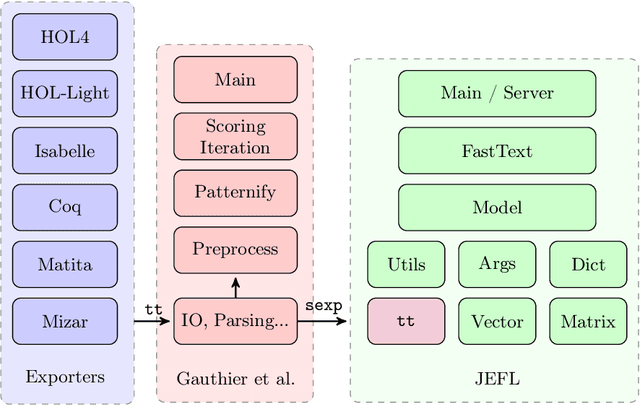
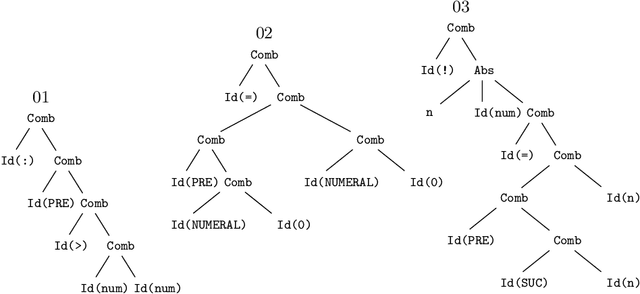
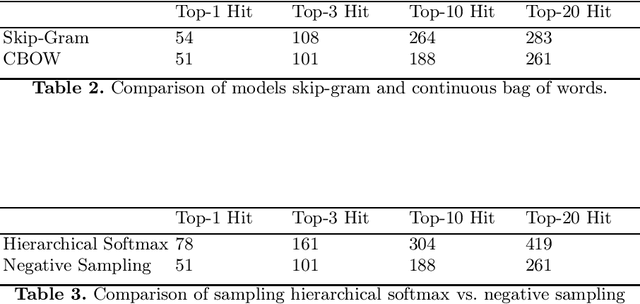
The heterogeneous nature of the logical foundations used in different interactive proof assistant libraries has rendered discovery of similar mathematical concepts among them difficult. In this paper, we compare a previously proposed algorithm for matching concepts across libraries with our unsupervised embedding approach that can help us retrieve similar concepts. Our approach is based on the fasttext implementation of Word2Vec, on top of which a tree traversal module is added to adapt its algorithm to the representation format of our data export pipeline. We compare the explainability, customizability, and online-servability of the approaches and argue that the neural embedding approach has more potential to be integrated into an interactive proof assistant.