Symmetry breaking for inductive logic programming

The goal of inductive logic programming is to search for a hypothesis that generalises training data and background knowledge. The challenge is searching vast hypothesis spaces, which is exacerbated because many logically equivalent hypotheses exist. To address this challenge, we introduce a method to break symmetries in the hypothesis space. We implement our idea in answer set programming. Our experiments on multiple domains, including visual reasoning and game playing, show that our approach can reduce solving times from over an hour to just 17 seconds.

Honey, I shrunk the hypothesis space (through logical preprocessing)

Inductive logic programming (ILP) is a form of logical machine learning. The goal is to search a hypothesis space for a hypothesis that generalises training examples and background knowledge. We introduce an approach that 'shrinks' the hypothesis space before an ILP system searches it. Our approach uses background knowledge to find rules that cannot be in an optimal hypothesis regardless of the training examples. For instance, our approach discovers relationships such as "even numbers cannot be odd" and "prime numbers greater than 2 are odd". It then removes violating rules from the hypothesis space. We implement our approach using answer set programming and use it to shrink the hypothesis space of a constraint-based ILP system. Our experiments on multiple domains, including visual reasoning and game playing, show that our approach can substantially reduce learning times whilst maintaining predictive accuracies. For instance, given just 10 seconds of preprocessing time, our approach can reduce learning times from over 10 hours to only 2 seconds.

Efficient rule induction by ignoring pointless rules

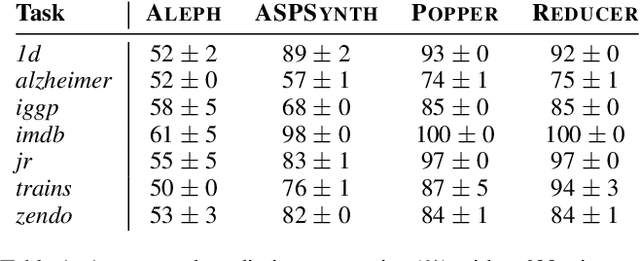
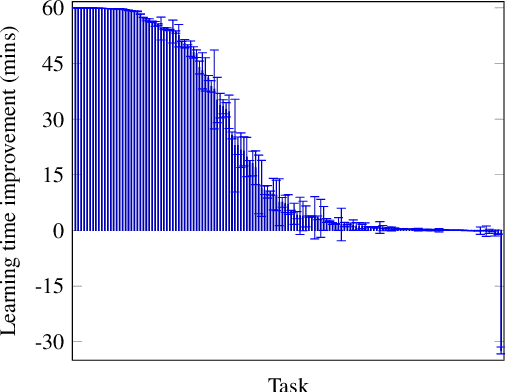
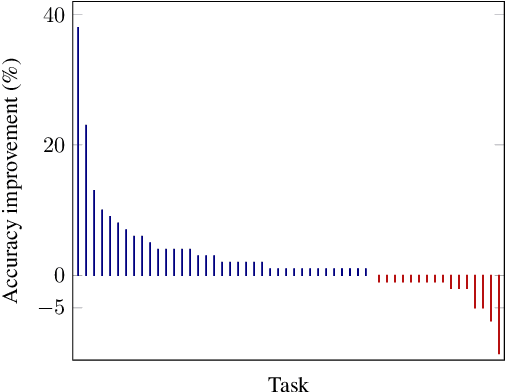
The goal of inductive logic programming (ILP) is to find a set of logical rules that generalises training examples and background knowledge. We introduce an ILP approach that identifies pointless rules. A rule is pointless if it contains a redundant literal or cannot discriminate against negative examples. We show that ignoring pointless rules allows an ILP system to soundly prune the hypothesis space. Our experiments on multiple domains, including visual reasoning and game playing, show that our approach can reduce learning times by 99% whilst maintaining predictive accuracies.

Learning Rules Explaining Interactive Theorem Proving Tactic Prediction

Formally verifying the correctness of mathematical proofs is more accessible than ever, however, the learning curve remains steep for many of the state-of-the-art interactive theorem provers (ITP). Deriving the most appropriate subsequent proof step, and reasoning about it, given the multitude of possibilities, remains a daunting task for novice users. To improve the situation, several investigations have developed machine learning based guidance for tactic selection. Such approaches struggle to learn non-trivial relationships between the chosen tactic and the structure of the proof state and represent them as symbolic expressions. To address these issues we (i) We represent the problem as an Inductive Logic Programming (ILP) task, (ii) Using the ILP representation we enriched the feature space by encoding additional, computationally expensive properties as background knowledge predicates, (iii) We use this enriched feature space to learn rules explaining when a tactic is applicable to a given proof state, (iv) we use the learned rules to filter the output of an existing tactic selection approach and empirically show improvement over the non-filtering approaches.

Scalable Knowledge Refactoring using Constrained Optimisation

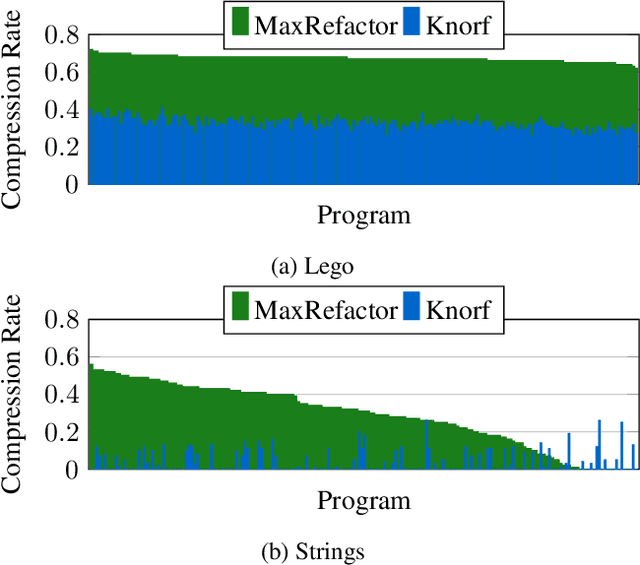
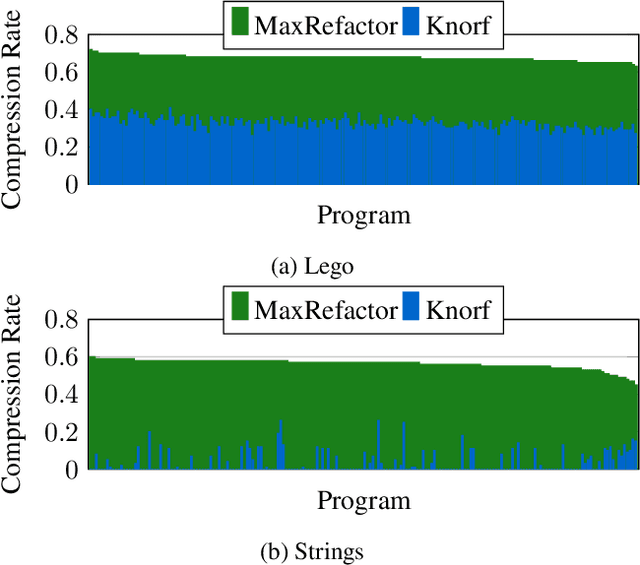
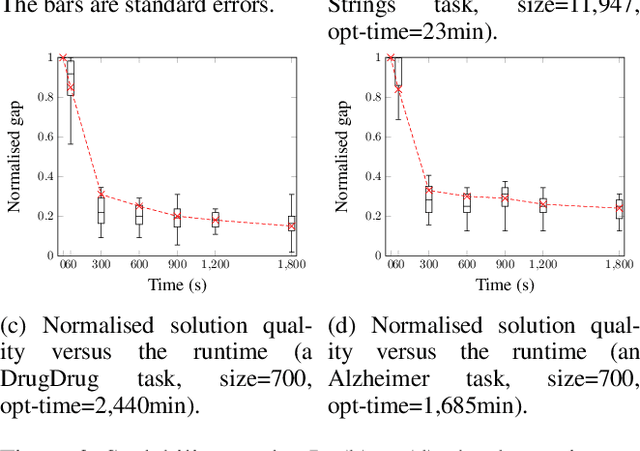
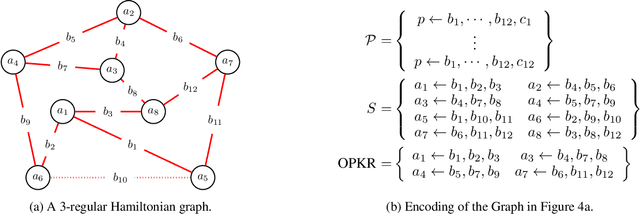
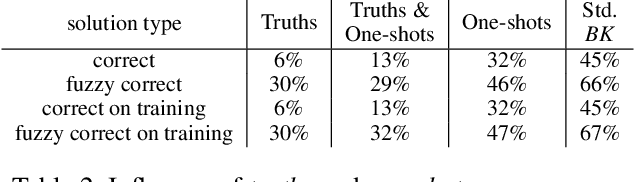
Knowledge refactoring compresses a logic program by introducing new rules. Current approaches struggle to scale to large programs. To overcome this limitation, we introduce a constrained optimisation refactoring approach. Our first key idea is to encode the problem with decision variables based on literals rather than rules. Our second key idea is to focus on linear invented rules. Our empirical results on multiple domains show that our approach can refactor programs quicker and with more compression than the previous state-of-the-art approach, sometimes by 60%.

Anti-unification and Generalization: A Survey

Anti-unification (AU), also known as generalization, is a fundamental operation used for inductive inference and is the dual operation to unification, an operation at the foundation of theorem proving. Interest in AU from the AI and related communities is growing, but without a systematic study of the concept, nor surveys of existing work, investigations7 often resort to developing application-specific methods that may be covered by existing approaches. We provide the first survey of AU research and its applications, together with a general framework for categorizing existing and future developments.

Generalisation Through Negation and Predicate Invention

The ability to generalise from a small number of examples is a fundamental challenge in machine learning. To tackle this challenge, we introduce an inductive logic programming (ILP) approach that combines negation and predicate invention. Combining these two features allows an ILP system to generalise better by learning rules with universally quantified body-only variables. We implement our idea in N OPI which can learn normal logic programs with negation and predicate invention, including Datalog with stratified negation. Our experimental results on multiple domains show that our approach improves predictive accuracies and learning times.

Differentiable Inductive Logic Programming in High-Dimensional Space

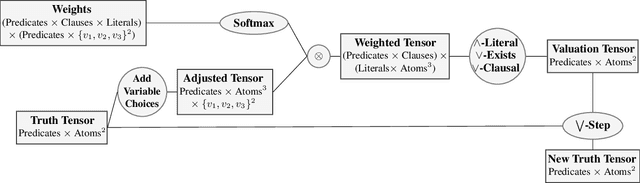
Synthesizing large logic programs through Inductive Logic Programming (ILP) typically requires intermediate definitions. However, cluttering the hypothesis space with intensional predicates often degrades performance. In contrast, gradient descent provides an efficient way to find solutions within such high-dimensional spaces. Neuro-symbolic ILP approaches have not fully exploited this so far. We propose an approach to ILP-based synthesis benefiting from large-scale predicate invention exploiting the efficacy of high-dimensional gradient descent. We find symbolic solutions containing upwards of ten auxiliary definitions. This is beyond the achievements of existing neuro-symbolic ILP systems, thus constituting a milestone in the field.

Learning Higher-Order Programs without Meta-Interpretive Learning

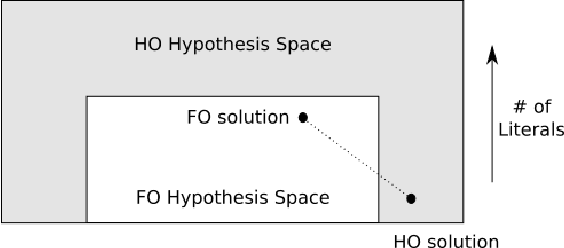
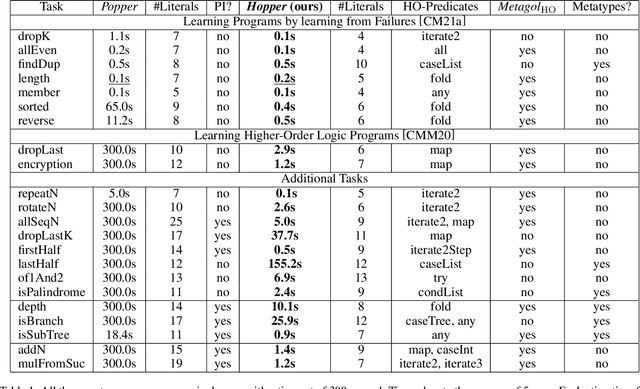
Learning complex programs through inductive logic programming (ILP) remains a formidable challenge. Existing higher-order enabled ILP systems show improved accuracy and learning performance, though remain hampered by the limitations of the underlying learning mechanism. Experimental results show that our extension of the versatile Learning From Failures paradigm by higher-order definitions significantly improves learning performance without the burdensome human guidance required by existing systems. Our theoretical framework captures a class of higher-order definitions preserving soundness of existing subsumption-based pruning methods.