Anti-unification and Generalization: A Survey

Anti-unification (AU), also known as generalization, is a fundamental operation used for inductive inference and is the dual operation to unification, an operation at the foundation of theorem proving. Interest in AU from the AI and related communities is growing, but without a systematic study of the concept, nor surveys of existing work, investigations7 often resort to developing application-specific methods that may be covered by existing approaches. We provide the first survey of AU research and its applications, together with a general framework for categorizing existing and future developments.

Proceedings of the 9th International Symposium on Symbolic Computation in Software Science

This volume contains papers presented at the Ninth International Symposium on Symbolic Computation in Software Science, SCSS 2021. Symbolic Computation is the science of computing with symbolic objects (terms, formulae, programs, representations of algebraic objects, etc.). Powerful algorithms have been developed during the past decades for the major subareas of symbolic computation: computer algebra and computational logic. These algorithms and methods are successfully applied in various fields, including software science, which covers a broad range of topics about software construction and analysis. Meanwhile, artificial intelligence methods and machine learning algorithms are widely used nowadays in various domains and, in particular, combined with symbolic computation. Several approaches mix artificial intelligence and symbolic methods and tools deployed over large corpora to create what is known as cognitive systems. Cognitive computing focuses on building systems that interact with humans naturally by reasoning, aiming at learning at scale. The purpose of SCSS is to promote research on theoretical and practical aspects of symbolic computation in software science, combined with modern artificial intelligence techniques. These proceedings contain the keynote paper by Bruno Buchberger and ten contributed papers. Besides, the conference program included three invited talks, nine short and work-in-progress papers, and a special session on computer algebra and computational logic. Due to the COVID-19 pandemic, the symposium was held completely online. It was organized by the Research Institute for Symbolic Computation (RISC) of the Johannes Kepler University Linz on September 8--10, 2021.

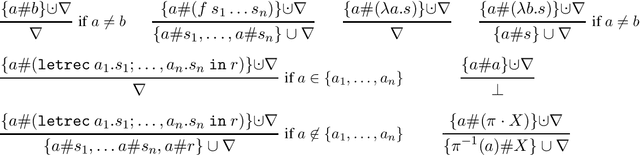
Nominal Unification and Matching of Higher Order Expressions with Recursive Let

A sound and complete algorithm for nominal unification of higher-order expressions with a recursive let is described, and shown to run in nondeterministic polynomial time. We also explore specializations like nominal letrec-matching for expressions, for DAGs, and for garbage-free expressions and determine their complexity. Finally, we also provide a nominal unification algorithm for higher-order expressions with recursive let and atom-variables, where we show that it also runs in nondeterministic polynomial time.