General Boolean Formula Minimization with QBF Solvers

The minimization of propositional formulae is a classical problem in logic, whose first algorithms date back at least to the 1950s with the works of Quine and Karnaugh. Most previous work in the area has focused on obtaining minimal, or quasi-minimal, formulae in conjunctive normal form (CNF) or disjunctive normal form (DNF), with applications in hardware design. In this paper, we are interested in the problem of obtaining an equivalent formula in any format, also allowing connectives that are not present in the original formula. We are primarily motivated in applying minimization algorithms to generate natural language translations of the original formula, where using shorter equivalents as input may result in better translations. Recently, Buchfuhrer and Umans have proved that the (decisional version of the) problem is $\Sigma_2^p$-complete. We analyze three possible (practical) approaches to solving the problem. First, using brute force, generating all possible formulae in increasing size and checking if they are equivalent to the original formula by testing all possible variable assignments. Second, generating the Tseitin coding of all the formulae and checking equivalence with the original using a SAT solver. Third, encoding the problem as a Quantified Boolean Formula (QBF), and using a QBF solver. Our results show that the QBF approach largely outperforms the other two.

Reducing SAT to Max2XOR

Representing some problems with XOR clauses (parity constraints) can allow to apply more efficient reasoning techniques. In this paper, we present a gadget for translating SAT clauses into Max2XOR constraints, i.e., XOR clauses of at most 2 variables equal to zero or to one. Additionally, we present new resolution rules for the Max2XOR problem which asks for which is the maximum number of constraints that can be satisfied from a set of 2XOR equations.

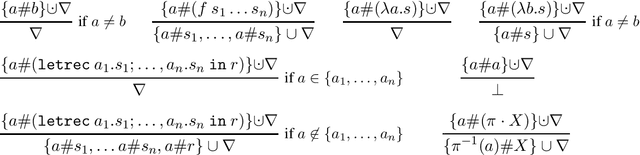
Nominal Unification and Matching of Higher Order Expressions with Recursive Let

A sound and complete algorithm for nominal unification of higher-order expressions with a recursive let is described, and shown to run in nondeterministic polynomial time. We also explore specializations like nominal letrec-matching for expressions, for DAGs, and for garbage-free expressions and determine their complexity. Finally, we also provide a nominal unification algorithm for higher-order expressions with recursive let and atom-variables, where we show that it also runs in nondeterministic polynomial time.

Community Structure in Industrial SAT Instances

Modern SAT solvers have experienced a remarkable progress on solving industrial instances. Most of the techniques have been developed after an intensive experimental process. It is believed that these techniques exploit the underlying structure of industrial instances. However, there are few works trying to exactly characterize the main features of this structure. The research community on complex networks has developed techniques of analysis and algorithms to study real-world graphs that can be used by the SAT community. Recently, there have been some attempts to analyze the structure of industrial SAT instances in terms of complex networks, with the aim of explaining the success of SAT solving techniques, and possibly improving them. In this paper, inspired by the results on complex networks, we study the community structure, or modularity, of industrial SAT instances. In a graph with clear community structure, or high modularity, we can find a partition of its nodes into communities such that most edges connect variables of the same community. In our analysis, we represent SAT instances as graphs, and we show that most application benchmarks are characterized by a high modularity. On the contrary, random SAT instances are closer to the classical Erd\"os-R\'enyi random graph model, where no structure can be observed. We also analyze how this structure evolves by the effects of the execution of the SAT solver. We detect that new clauses learnt by the solver during the search contribute to destroy the original community structure of the formula. This partially explains the distinct performance of SAT solvers on random and industrial SAT instances.