Exploiting Configurations of MaxSAT Solvers

In this paper, we describe how we can effectively exploit alternative parameter configurations to a MaxSAT solver. We describe how these configurations can be computed in the context of MaxSAT. In particular, we experimentally show how to easily combine configurations of a non-competitive solver to obtain a better solving approach.

Reducing SAT to Max2XOR

Representing some problems with XOR clauses (parity constraints) can allow to apply more efficient reasoning techniques. In this paper, we present a gadget for translating SAT clauses into Max2XOR constraints, i.e., XOR clauses of at most 2 variables equal to zero or to one. Additionally, we present new resolution rules for the Max2XOR problem which asks for which is the maximum number of constraints that can be satisfied from a set of 2XOR equations.

Incomplete MaxSAT Approaches for Combinatorial Testing

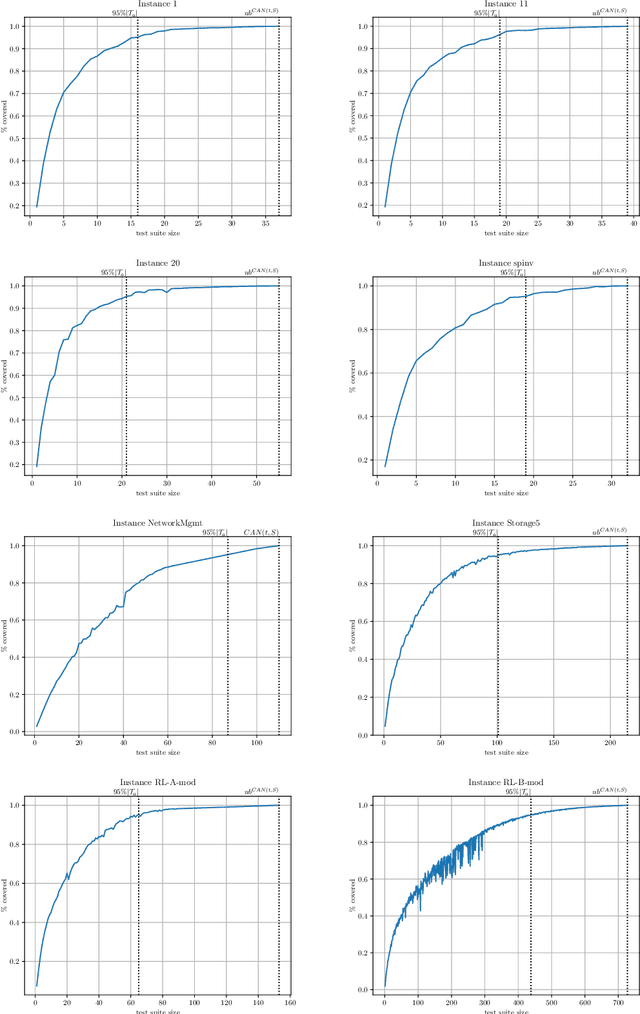
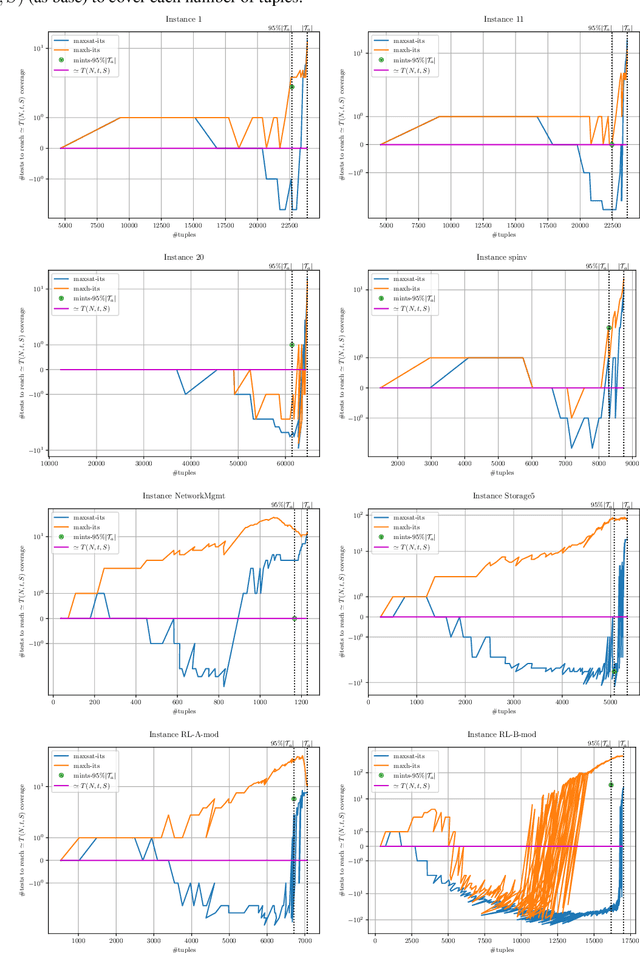
We present a Satisfiability (SAT)-based approach for building Mixed Covering Arrays with Constraints of minimum length, referred to as the Covering Array Number problem. This problem is central in Combinatorial Testing for the detection of system failures. In particular, we show how to apply Maximum Satisfiability (MaxSAT) technology by describing efficient encodings for different classes of complete and incomplete MaxSAT solvers to compute optimal and suboptimal solutions, respectively. Similarly, we show how to solve through MaxSAT technology a closely related problem, the Tuple Number problem, which we extend to incorporate constraints. For this problem, we additionally provide a new MaxSAT-based incomplete algorithm. The extensive experimental evaluation we carry out on the available Mixed Covering Arrays with Constraints benchmarks and the comparison with state-of-the-art tools confirm the good performance of our approaches.

Community Structure in Industrial SAT Instances

Modern SAT solvers have experienced a remarkable progress on solving industrial instances. Most of the techniques have been developed after an intensive experimental process. It is believed that these techniques exploit the underlying structure of industrial instances. However, there are few works trying to exactly characterize the main features of this structure. The research community on complex networks has developed techniques of analysis and algorithms to study real-world graphs that can be used by the SAT community. Recently, there have been some attempts to analyze the structure of industrial SAT instances in terms of complex networks, with the aim of explaining the success of SAT solving techniques, and possibly improving them. In this paper, inspired by the results on complex networks, we study the community structure, or modularity, of industrial SAT instances. In a graph with clear community structure, or high modularity, we can find a partition of its nodes into communities such that most edges connect variables of the same community. In our analysis, we represent SAT instances as graphs, and we show that most application benchmarks are characterized by a high modularity. On the contrary, random SAT instances are closer to the classical Erd\"os-R\'enyi random graph model, where no structure can be observed. We also analyze how this structure evolves by the effects of the execution of the SAT solver. We detect that new clauses learnt by the solver during the search contribute to destroy the original community structure of the formula. This partially explains the distinct performance of SAT solvers on random and industrial SAT instances.