Exploiting Configurations of MaxSAT Solvers

In this paper, we describe how we can effectively exploit alternative parameter configurations to a MaxSAT solver. We describe how these configurations can be computed in the context of MaxSAT. In particular, we experimentally show how to easily combine configurations of a non-competitive solver to obtain a better solving approach.

Learning Optimal Decision Trees Using MaxSAT

We present a Combinatorial Optimization approach based on Maximum Satisfiability technology to compute Minimum Pure Decision Trees (MPDTs) for the sake of interpretability. We show that our approach outperforms clearly in terms of runtime previous approaches to compute MPDTs. We additionally show that these MPDTs can outperform on average the DT classifiers generated with sklearn in terms of accuracy. Therefore, our approach tackles favourably the challenge of balancing interpretability and accuracy.

Incomplete MaxSAT Approaches for Combinatorial Testing

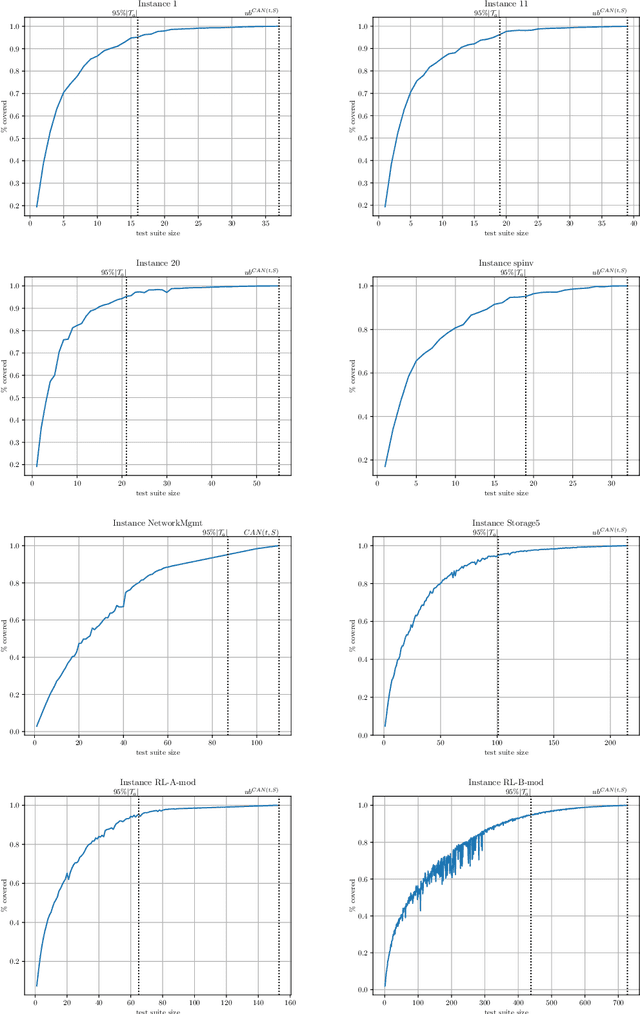
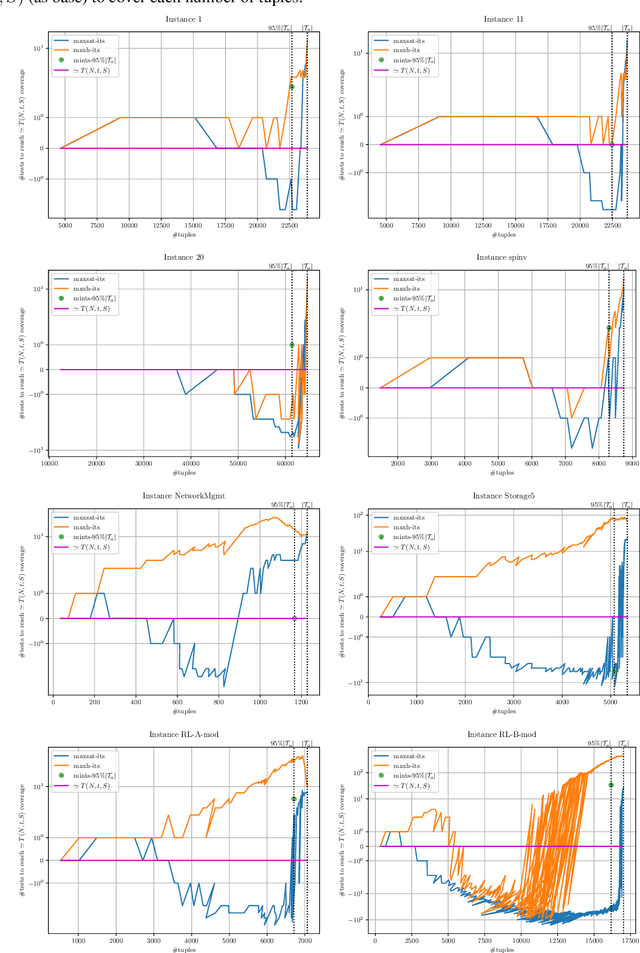
We present a Satisfiability (SAT)-based approach for building Mixed Covering Arrays with Constraints of minimum length, referred to as the Covering Array Number problem. This problem is central in Combinatorial Testing for the detection of system failures. In particular, we show how to apply Maximum Satisfiability (MaxSAT) technology by describing efficient encodings for different classes of complete and incomplete MaxSAT solvers to compute optimal and suboptimal solutions, respectively. Similarly, we show how to solve through MaxSAT technology a closely related problem, the Tuple Number problem, which we extend to incorporate constraints. For this problem, we additionally provide a new MaxSAT-based incomplete algorithm. The extensive experimental evaluation we carry out on the available Mixed Covering Arrays with Constraints benchmarks and the comparison with state-of-the-art tools confirm the good performance of our approaches.