Incorporating Multi-armed Bandit with Local Search for MaxSAT

Partial MaxSAT (PMS) and Weighted PMS (WPMS) are two practical generalizations of the MaxSAT problem. In this paper, we propose a local search algorithm for these problems, called BandHS, which applies two multi-armed bandits to guide the search directions when escaping local optima. One bandit is combined with all the soft clauses to help the algorithm select to satisfy appropriate soft clauses, and the other bandit with all the literals in hard clauses to help the algorithm select appropriate literals to satisfy the hard clauses. These two bandits can improve the algorithm's search ability in both feasible and infeasible solution spaces. We further propose an initialization method for (W)PMS that prioritizes both unit and binary clauses when producing the initial solutions. Extensive experiments demonstrate the excellent performance and generalization capability of our proposed methods, that greatly boost the state-of-the-art local search algorithm, SATLike3.0, and the state-of-the-art SAT-based incomplete solver, NuWLS-c.

Incomplete MaxSAT Approaches for Combinatorial Testing

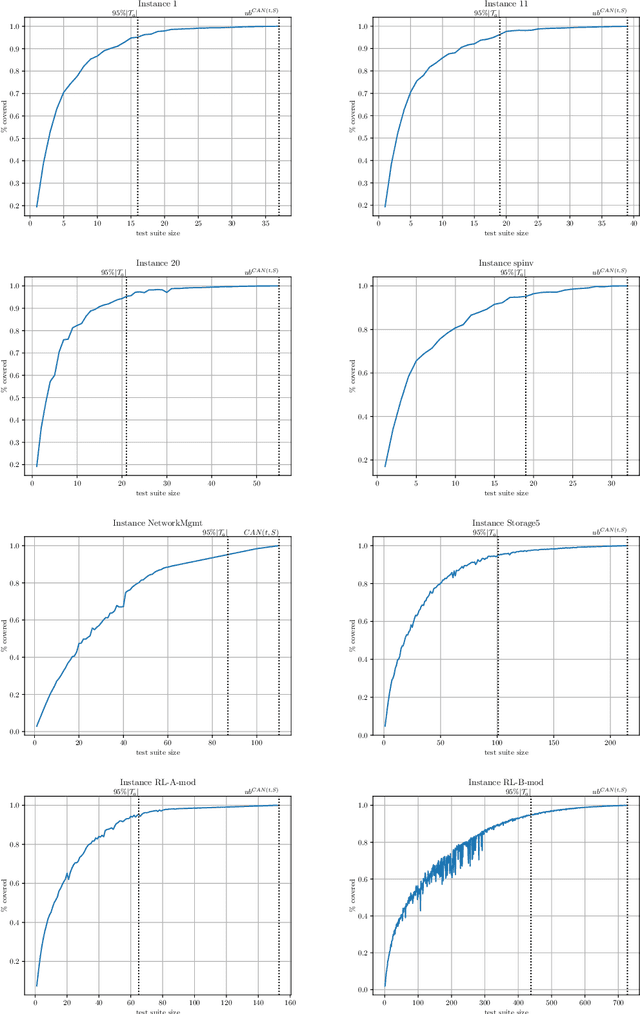
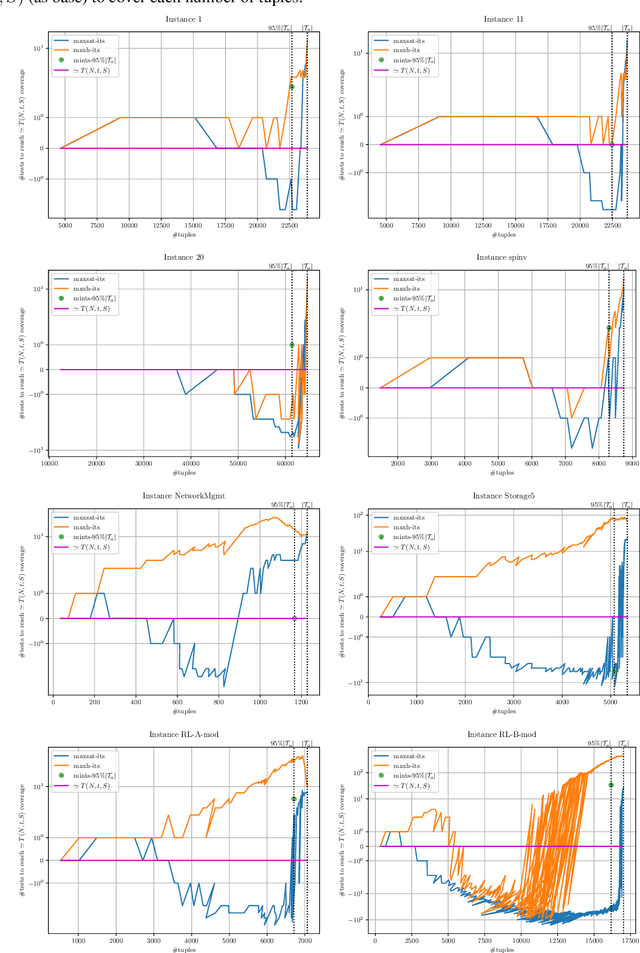
We present a Satisfiability (SAT)-based approach for building Mixed Covering Arrays with Constraints of minimum length, referred to as the Covering Array Number problem. This problem is central in Combinatorial Testing for the detection of system failures. In particular, we show how to apply Maximum Satisfiability (MaxSAT) technology by describing efficient encodings for different classes of complete and incomplete MaxSAT solvers to compute optimal and suboptimal solutions, respectively. Similarly, we show how to solve through MaxSAT technology a closely related problem, the Tuple Number problem, which we extend to incorporate constraints. For this problem, we additionally provide a new MaxSAT-based incomplete algorithm. The extensive experimental evaluation we carry out on the available Mixed Covering Arrays with Constraints benchmarks and the comparison with state-of-the-art tools confirm the good performance of our approaches.

Clause Vivification by Unit Propagation in CDCL SAT Solvers

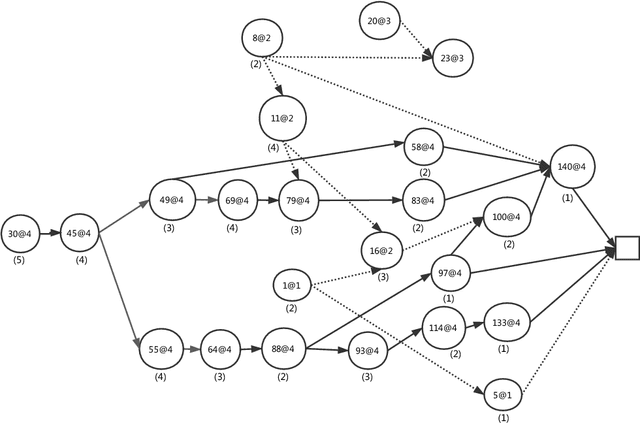
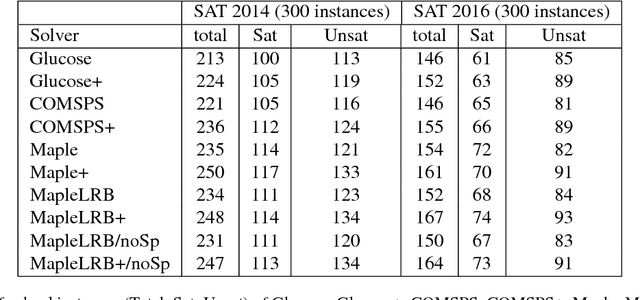
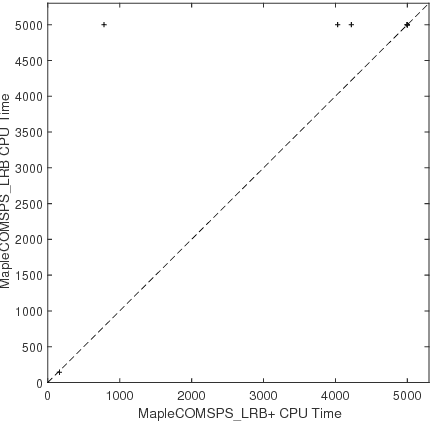
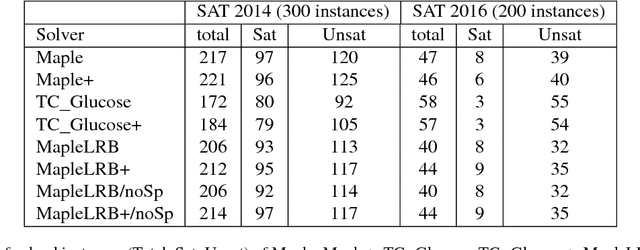
Original and learnt clauses in Conflict-Driven Clause Learning (CDCL) SAT solvers often contain redundant literals. This may have a negative impact on performance because redundant literals may deteriorate both the effectiveness of Boolean constraint propagation and the quality of subsequent learnt clauses. To overcome this drawback, we propose a clause vivification approach that eliminates redundant literals by applying unit propagation. The proposed clause vivification is activated before the SAT solver triggers some selected restarts, and only affects a subset of original and learnt clauses, which are considered to be more relevant according to metrics like the literal block distance (LBD). Moreover, we conducted an empirical investigation with instances coming from the hard combinatorial and application categories of recent SAT competitions. The results show that a remarkable number of additional instances are solved when the proposed approach is incorporated into five of the best performing CDCL SAT solvers (Glucose, TC_Glucose, COMiniSatPS, MapleCOMSPS and MapleCOMSPS_LRB). More importantly, the empirical investigation includes an in-depth analysis of the effectiveness of clause vivification. It is worth mentioning that one of the SAT solvers described here was ranked first in the main track of SAT Competition 2017 thanks to the incorporation of the proposed clause vivification. That solver was further improved in this paper and won the bronze medal in the main track of SAT Competition 2018.