FIMP-HGA: A Novel Approach to Addressing the Partitioning Min-Max Weighted Matching Problem

The Partitioning Min-Max Weighted Matching (PMMWM) problem, being a practical NP-hard problem, integrates the task of partitioning the vertices of a bipartite graph into disjoint sets of limited size with the classical Maximum-Weight Perfect Matching (MPWM) problem. Initially introduced in 2015, the state-of-the-art method for addressing PMMWM is the MP$_{\text{LS}}$. In this paper, we present a novel approach, the Fast Iterative Match-Partition Hybrid Genetic Algorithm (FIMP-HGA), for addressing PMMWM. Similar to MP$_{\text{LS}}$, FIMP-HGA divides the solving into match and partition stages, iteratively refining the solution. In the match stage, we propose the KM-M algorithm, which reduces matching complexity through incremental adjustments, significantly enhancing runtime efficiency. For the partition stage, we introduce a Hybrid Genetic Algorithm (HGA) incorporating an elite strategy and design a Greedy Partition Crossover (GPX) operator alongside a Multilevel Local Search (MLS) to optimize individuals in the population. Population initialization employs various methods, including the multi-way Karmarkar-Karp (KK) algorithm, ensuring both quality and diversity. At each iteration, the bipartite graph is adjusted based on the current solution, aiming for continuous improvement. To conduct comprehensive experiments, we develop a new instance generation method compatible with existing approaches, resulting in four benchmark groups. Extensive experiments evaluate various algorithm modules, accurately assessing each module's impact on improvement. Evaluation results on our benchmarks demonstrate that the proposed FIMP-HGA significantly enhances solution quality compared to MP$_{\text{LS}}$, meanwhile reducing runtime by 3 to 20 times.

An Effective Branch-and-Bound Algorithm with New Bounding Methods for the Maximum $s$-Bundle Problem

The Maximum s-Bundle Problem (MBP) addresses the task of identifying a maximum s-bundle in a given graph. A graph G=(V, E) is called an s-bundle if its vertex connectivity is at least |V|-s, where the vertex connectivity equals the minimum number of vertices whose deletion yields a disconnected or trivial graph. MBP is NP-hard and holds relevance in numerous realworld scenarios emphasizing the vertex connectivity. Exact algorithms for MBP mainly follow the branch-and-bound (BnB) framework, whose performance heavily depends on the quality of the upper bound on the cardinality of a maximum s-bundle and the initial lower bound with graph reduction. In this work, we introduce a novel Partition-based Upper Bound (PUB) that leverages the graph partitioning technique to achieve a tighter upper bound compared to existing ones. To increase the lower bound, we propose to do short random walks on a clique to generate larger initial solutions. Then, we propose a new BnB algorithm that uses the initial lower bound and PUB in preprocessing for graph reduction, and uses PUB in the BnB search process for branch pruning. Extensive experiments with diverse s values demonstrate the significant progress of our algorithm over state-of-the-art BnB MBP algorithms. Moreover, our initial lower bound can also be generalized to other relaxation clique problems.

Rethinking the Soft Conflict Pseudo Boolean Constraint on MaxSAT Local Search Solvers

MaxSAT is an optimization version of the famous NP-complete Satisfiability problem (SAT). Algorithms for MaxSAT mainly include complete solvers and local search incomplete solvers. In many complete solvers, once a better solution is found, a Soft conflict Pseudo Boolean (SPB) constraint will be generated to enforce the algorithm to find better solutions. In many local search algorithms, clause weighting is a key technique for effectively guiding the search directions. In this paper, we propose to transfer the SPB constraint into the clause weighting system of the local search method, leading the algorithm to better solutions. We further propose an adaptive clause weighting strategy that breaks the tradition of using constant values to adjust clause weights. Based on the above methods, we propose a new local search algorithm called SPB-MaxSAT that provides new perspectives for clause weighting on MaxSAT local search solvers. Extensive experiments demonstrate the excellent performance of the proposed methods.

Incorporating Multi-armed Bandit with Local Search for MaxSAT

Partial MaxSAT (PMS) and Weighted PMS (WPMS) are two practical generalizations of the MaxSAT problem. In this paper, we propose a local search algorithm for these problems, called BandHS, which applies two multi-armed bandits to guide the search directions when escaping local optima. One bandit is combined with all the soft clauses to help the algorithm select to satisfy appropriate soft clauses, and the other bandit with all the literals in hard clauses to help the algorithm select appropriate literals to satisfy the hard clauses. These two bandits can improve the algorithm's search ability in both feasible and infeasible solution spaces. We further propose an initialization method for (W)PMS that prioritizes both unit and binary clauses when producing the initial solutions. Extensive experiments demonstrate the excellent performance and generalization capability of our proposed methods, that greatly boost the state-of-the-art local search algorithm, SATLike3.0, and the state-of-the-art SAT-based incomplete solver, NuWLS-c.

Reinforced Lin-Kernighan-Helsgaun Algorithms for the Traveling Salesman Problems

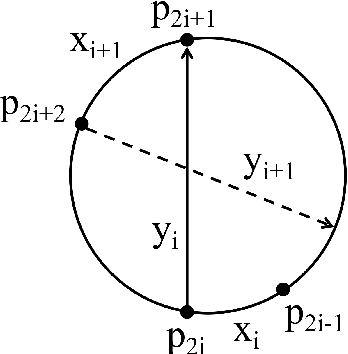
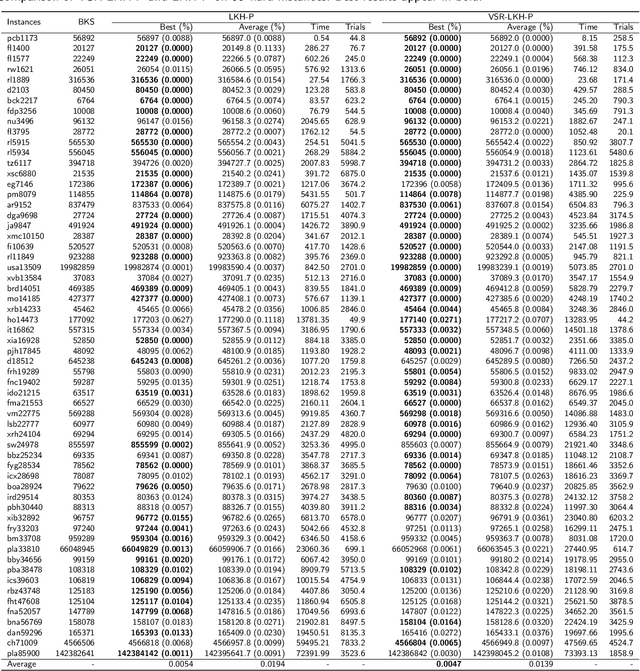
TSP is a classical NP-hard combinatorial optimization problem with many practical variants. LKH is one of the state-of-the-art local search algorithms for the TSP. LKH-3 is a powerful extension of LKH that can solve many TSP variants. Both LKH and LKH-3 associate a candidate set to each city to improve the efficiency, and have two different methods, $\alpha$-measure and POPMUSIC, to decide the candidate sets. In this work, we first propose a Variable Strategy Reinforced LKH (VSR-LKH) algorithm, which incorporates three reinforcement learning methods (Q-learning, Sarsa, Monte Carlo) with LKH, for the TSP. We further propose a new algorithm called VSR-LKH-3 that combines the variable strategy reinforcement learning method with LKH-3 for typical TSP variants, including the TSP with time windows (TSPTW) and Colored TSP (CTSP). The proposed algorithms replace the inflexible traversal operations in LKH and LKH-3 and let the algorithms learn to make a choice at each search step by reinforcement learning. Both LKH and LKH-3, with either $\alpha$-measure or POPMUSIC, can be significantly improved by our methods. Extensive experiments on 236 widely-used TSP benchmarks with up to 85,900 cities demonstrate the excellent performance of VSR-LKH. VSR-LKH-3 also significantly outperforms the state-of-the-art heuristics for TSPTW and CTSP.

An Effective Iterated Two-stage Heuristic Algorithm for the Multiple Traveling Salesmen Problem

The multiple Traveling Salesmen Problem mTSP is a general extension of the famous NP-hard Traveling Salesmen Problem (TSP), that there are m (m>1) salesmen to visit the cities. In this paper, we address the mTSP with both of the minsum objective and the minmax objective, which aims at minimizing the total length of the m tours and the length of the longest tour among all the m tours, respectively. We propose an iterated two-stage heuristic algorithm, denoted as ITSHA. Each iteration of ITSHA consists of an initialization stage and an improvement stage. The purpose of the initialization stage is to generate high-quality and diverse initial solutions. The improvement stage mainly applies the variable neighborhood search (VNS) approach based on our proposed local search neighborhoods to optimize the initial solution generated by the initialization stage. Moreover, some local optima escaping approaches are employed to enhance the search ability of the algorithm. Extensive experimental results on a wide range of public benchmark instances show that ITSHA significantly outperforms state-of-the-art heuristic algorithms in solving the mTSP on both the objectives.

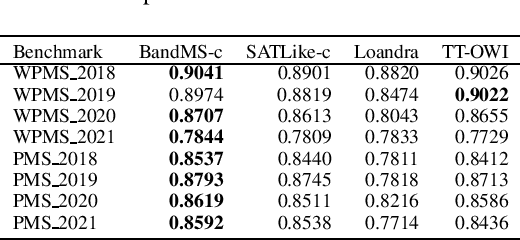
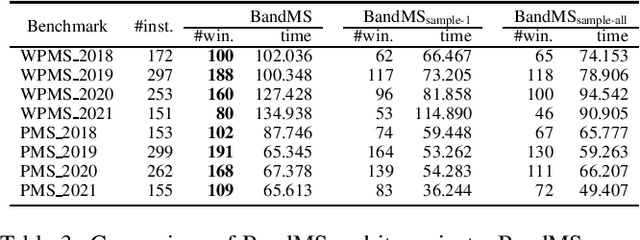
BandMaxSAT: A Local Search MaxSAT Solver with Multi-armed Bandit

We address Partial MaxSAT (PMS) and Weighted PMS (WPMS), two practical generalizations of the MaxSAT problem, and propose a local search algorithm called BandMaxSAT, that applies a multi-armed bandit to guide the search direction, for these problems. The bandit in our method is associated with all the soft clauses in the input (W)PMS instance. Each arm corresponds to a soft clause. The bandit model can help BandMaxSAT to select a good direction to escape from local optima by selecting a soft clause to be satisfied in the current step, that is, selecting an arm to be pulled. We further propose an initialization method for (W)PMS that prioritizes both unit and binary clauses when producing the initial solutions. Extensive experiments demonstrate that BandMaxSAT significantly outperforms the state-of-the-art (W)PMS local search algorithm SATLike3.0. Specifically, the number of instances in which BandMaxSAT obtains better results is about twice that obtained by SATLike3.0. We further combine BandMaxSAT with the complete solver TT-Open-WBO-Inc. The resulting solver BandMaxSAT-c also outperforms some of the best state-of-the-art complete (W)PMS solvers, including SATLike-c, Loandra and TT-Open-WBO-Inc.

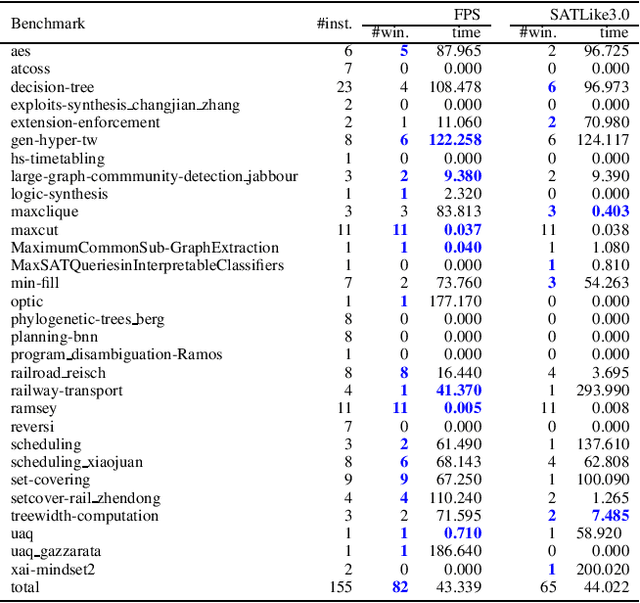
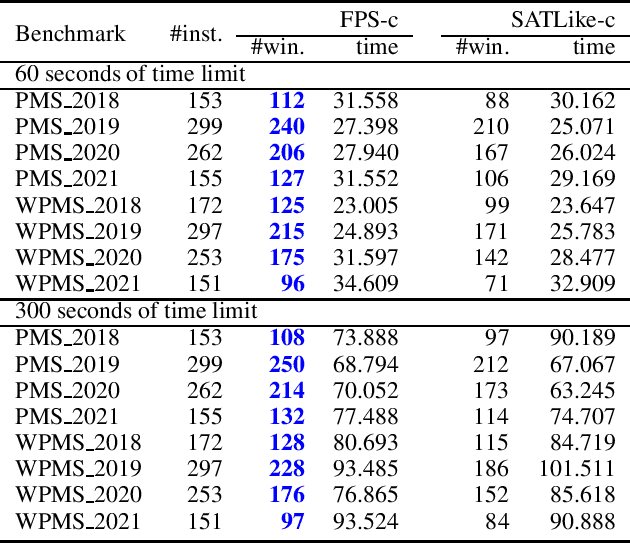
Farsighted Probabilistic Sampling based Local Search for (Weighted) Partial MaxSAT

Partial MaxSAT (PMS) and Weighted Partial MaxSAT (WPMS) are both practical generalizations to the typical combinatorial problem of MaxSAT. In this work, we propose an effective farsighted probabilistic sampling based local search algorithm called FPS for solving these two problems, denoted as (W)PMS. The FPS algorithm replaces the mechanism of flipping a single variable per iteration step, that is widely used in existing (W)PMS local search algorithms, with the proposed farsighted local search strategy, and provides higher-quality local optimal solutions. The farsighted strategy employs the probabilistic sampling technique that allows the algorithm to look-ahead widely and efficiently. In this way, FPS can provide more and better search directions and improve the performance without reducing the efficiency. Extensive experiments on all the benchmarks of (W)PMS problems from the incomplete track of recent four years of MaxSAT Evaluations demonstrate that our method significantly outperforms SATLike3.0, the state-of-the-art local search algorithm, for solving both the PMS and WPMS problems. We furthermore do comparison with the extended solver of SATLike, SATLike-c, which is the champion of three categories among the total four (PMS and WPMS categories, each associated with two time limits) of the incomplete track in the recent MaxSAT Evaluation (MSE2021). We replace the local search component in SATLike-c with the proposed farsighted sampling local search approach, and the resulting solver FPS-c also outperforms SATLike-c for solving both the PMS and WPMS problems.

Reinforced Hybrid Genetic Algorithm for the Traveling Salesman Problem

We propose a powerful Reinforced Hybrid Genetic Algorithm (RHGA) for the famous NP-hard Traveling Salesman Problem (TSP). RHGA combines reinforcement learning technique with the well-known Edge Assembly Crossover genetic algorithm (EAX-GA) and the Lin-Kernighan-Helsgaun (LKH) local search heuristic. With the help of the proposed hybrid mechanism, the genetic evolution of EAX-GA and the local search of LKH can boost each other's performance. And the reinforcement learning technique based on Q-learning further promotes the hybrid genetic algorithm. Experimental results on 138 well-known and widely used TSP benchmarks, with the number of cities ranging from 1,000 to 85,900, demonstrate the excellent performance of the proposed method.

Combining Reinforcement Learning with Lin-Kernighan-Helsgaun Algorithm for the Traveling Salesman Problem

We address the Traveling Salesman Problem (TSP), a famous NP-hard combinatorial optimization problem. And we propose a variable strategy reinforced approach, denoted as VSR-LKH, which combines three reinforcement learning methods (Q-learning, Sarsa and Monte Carlo) with the well-known TSP algorithm, called Lin-Kernighan-Helsgaun (LKH). VSR-LKH replaces the inflexible traversal operation in LKH, and lets the program learn to make choice at each search step by reinforcement learning. Experimental results on 111 TSP benchmarks from the TSPLIB with up to 85,900 cities demonstrate the excellent performance of the proposed method.