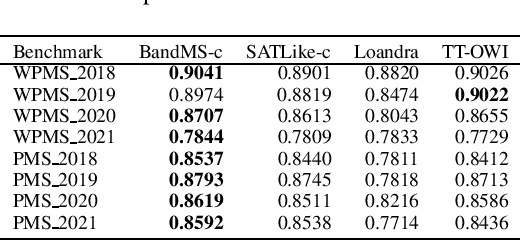
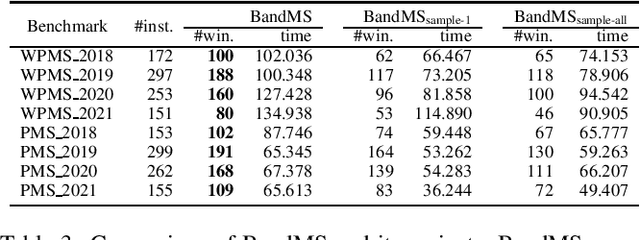
BandMaxSAT: A Local Search MaxSAT Solver with Multi-armed Bandit

We address Partial MaxSAT (PMS) and Weighted PMS (WPMS), two practical generalizations of the MaxSAT problem, and propose a local search algorithm called BandMaxSAT, that applies a multi-armed bandit to guide the search direction, for these problems. The bandit in our method is associated with all the soft clauses in the input (W)PMS instance. Each arm corresponds to a soft clause. The bandit model can help BandMaxSAT to select a good direction to escape from local optima by selecting a soft clause to be satisfied in the current step, that is, selecting an arm to be pulled. We further propose an initialization method for (W)PMS that prioritizes both unit and binary clauses when producing the initial solutions. Extensive experiments demonstrate that BandMaxSAT significantly outperforms the state-of-the-art (W)PMS local search algorithm SATLike3.0. Specifically, the number of instances in which BandMaxSAT obtains better results is about twice that obtained by SATLike3.0. We further combine BandMaxSAT with the complete solver TT-Open-WBO-Inc. The resulting solver BandMaxSAT-c also outperforms some of the best state-of-the-art complete (W)PMS solvers, including SATLike-c, Loandra and TT-Open-WBO-Inc.

Combining Reinforcement Learning with Lin-Kernighan-Helsgaun Algorithm for the Traveling Salesman Problem

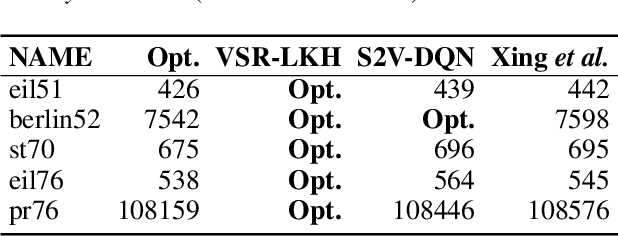
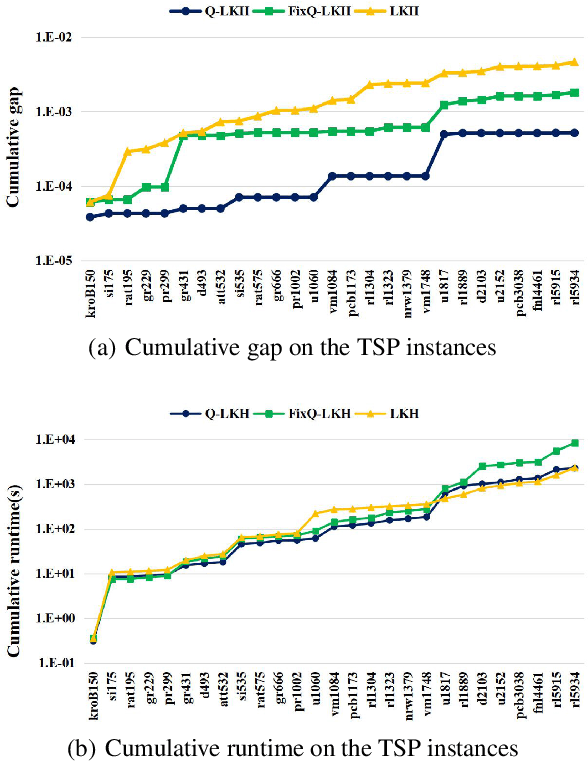
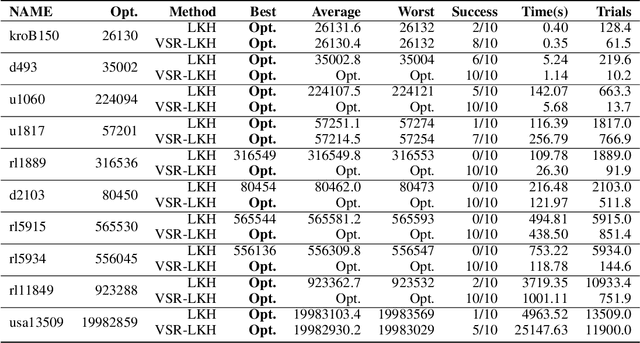
We address the Traveling Salesman Problem (TSP), a famous NP-hard combinatorial optimization problem. And we propose a variable strategy reinforced approach, denoted as VSR-LKH, which combines three reinforcement learning methods (Q-learning, Sarsa and Monte Carlo) with the well-known TSP algorithm, called Lin-Kernighan-Helsgaun (LKH). VSR-LKH replaces the inflexible traversal operation in LKH, and lets the program learn to make choice at each search step by reinforcement learning. Experimental results on 111 TSP benchmarks from the TSPLIB with up to 85,900 cities demonstrate the excellent performance of the proposed method.

Stochastic Item Descent Method for Large Scale Equal Circle Packing Problem

Stochastic gradient descent (SGD) is a powerful method for large-scale optimization problems in the area of machine learning, especially for a finite-sum formulation with numerous variables. In recent years, mini-batch SGD gains great success and has become a standard technique for training deep neural networks fed with big amount of data. Inspired by its success in deep learning, we apply the idea of SGD with batch selection of samples to a classic optimization problem in decision version. Given $n$ unit circles, the equal circle packing problem (ECPP) asks whether there exist a feasible packing that could put all the circles inside a circular container without overlapping. Specifically, we propose a stochastic item descent method (SIDM) for ECPP in large scale, which randomly divides the unit circles into batches and runs Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm on the corresponding batch function iteratively to speedup the calculation. We also increase the batch size during the batch iterations to gain higher quality solution. Comparing to the current best packing algorithms, SIDM greatly speeds up the calculation of optimization process and guarantees the solution quality for large scale instances with up to 1500 circle items, while the baseline algorithms usually handle about 300 circle items. The results indicate the highly efficiency of SIDM for this classic optimization problem in large scale, and show potential for other large scale classic optimization problems in which gradient descent is used for optimization.

A Learning based Branch and Bound for Maximum Common Subgraph Problems

Branch-and-bound (BnB) algorithms are widely used to solve combinatorial problems, and the performance crucially depends on its branching heuristic.In this work, we consider a typical problem of maximum common subgraph (MCS), and propose a branching heuristic inspired from reinforcement learning with a goal of reaching a tree leaf as early as possible to greatly reduce the search tree size.Extensive experiments show that our method is beneficial and outperforms current best BnB algorithm for the MCS.