Towards a Model of Puzznic

We report on progress in modelling and solving Puzznic, a video game requiring the player to plan sequences of moves to clear a grid by matching blocks. We focus here on levels with no moving blocks. We compare a planning approach and three constraint programming approaches on a small set of benchmark instances. The planning approach is at present superior to the constraint programming approaches, but we outline proposals for improving the constraint models.

On Grid Graph Reachability and Puzzle Games

Many puzzle video games, like Sokoban, involve moving some agent in a maze. The reachable locations are usually apparent for a human player, and the difficulty of the game is mainly related to performing actions on objects, such as pushing (reachable) boxes. For this reason, the difficulty of a particular level is often measured as the number of actions on objects, other than agent walking, needed to find a solution. In this paper we study CP and SAT approaches for solving these kind of problems. We review some reachability encodings and propose a new one. We empirically show that the new encoding is well-suited for solving puzzle problems in the planning as SAT paradigm, especially when considering the execution of several actions in parallel.

A Good Snowman is Hard to Plan

In this work we face a challenging puzzle video game: A Good Snowman is Hard to Build. The objective of the game is to build snowmen by moving and stacking snowballs on a discrete grid. For the sake of player engagement with the game, it is interesting to avoid that a player finds a much easier solution than the one the designer expected. Therefore, having tools that are able to certify the optimality of solutions is crucial. Although the game can be stated as a planning problem and can be naturally modelled in PDDL, we show that a direct translation to SAT clearly outperforms off-the-shelf state-of-the-art planners. As we show, this is mainly due to the fact that reachability properties can be easily modelled in SAT, allowing for shorter plans, whereas using axioms to express a reachability derived predicate in PDDL does not result in any significant reduction of solving time with the considered planners. We deal with a set of 51 levels, both original and crafted, solving 43 and with 8 challenging instances still remaining to be solved.

Challenges in Modelling and Solving Plotting with PDDL

We study a planning problem based on Plotting, a tile-matching puzzle video game published by Taito in 1989. The objective of this game is to remove a target number of coloured blocks from a grid by sequentially shooting blocks into the grid. Plotting features complex transitions after every shot: various blocks are affected directly, while others can be indirectly affected by gravity. We highlight the challenges of modelling Plotting with PDDL and of solving it with a grounding-based state-of-the-art planner.

A Preliminary Case Study of Planning With Complex Transitions: Plotting

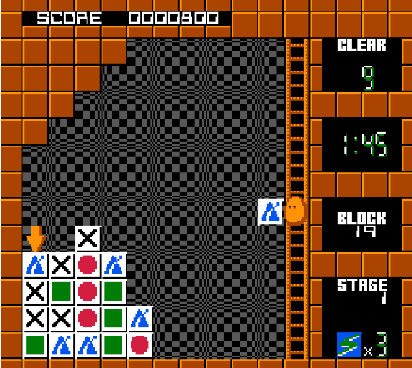
Plotting is a tile-matching puzzle video game published by Taito in 1989. Its objective is to reduce a given grid of coloured blocks down to a goal number or fewer. This is achieved by the avatar character repeatedly shooting the block it holds into the grid. Plotting is an example of a planning problem: given a model of the environment, a planning problem asks us to find a sequence of actions that can lead from an initial state of the environment to a given goal state while respecting some constraints. The key difficulty in modelling Plotting is in capturing the way the puzzle state changes after each shot. A single shot can affect multiple tiles directly, and the grid is affected by gravity so numerous other tiles can be affected indirectly. We present and evaluate a constraint model of the Plotting problem that captures this complexity. We also discuss the difficulties and inefficiencies of modelling Plotting in PDDL, the standard language used for input to specialised AI planners. We conclude by arguing that AI planning could benefit from a richer modelling language.

SAT Encodings for Pseudo-Boolean Constraints Together With At-Most-One Constraints

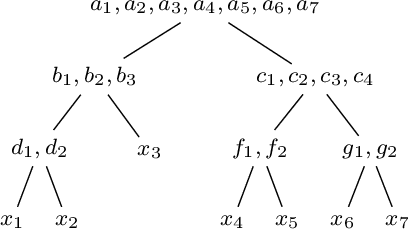
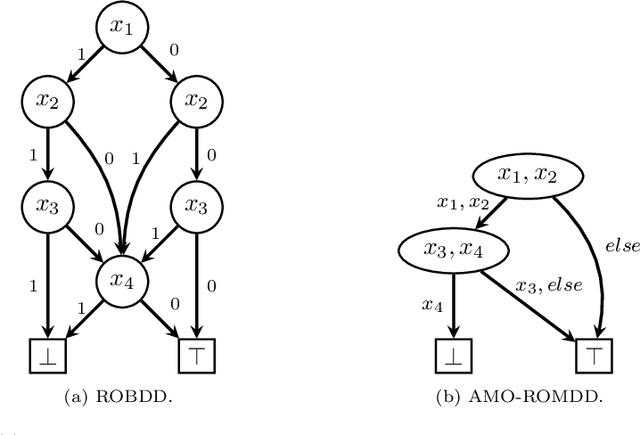
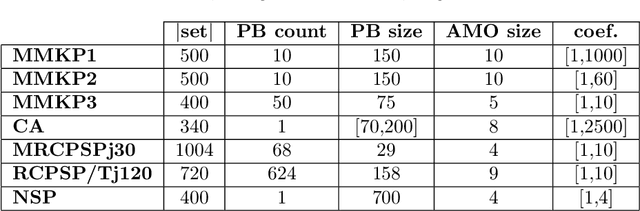
When solving a combinatorial problem using propositional satisfiability (SAT), the encoding of the problem is of vital importance. We study encodings of Pseudo-Boolean (PB) constraints, a common type of arithmetic constraint that appears in a wide variety of combinatorial problems such as timetabling, scheduling, and resource allocation. In some cases PB constraints occur together with at-most-one (AMO) constraints over subsets of their variables (forming PB(AMO) constraints). Recent work has shown that taking account of AMOs when encoding PB constraints using decision diagrams can produce a dramatic improvement in solver efficiency. In this paper we extend the approach to other state-of-the-art encodings of PB constraints, developing several new encodings for PB(AMO) constraints. Also, we present a more compact and efficient version of the popular Generalized Totalizer encoding, named Reduced Generalized Totalizer. This new encoding is also adapted for PB(AMO) constraints for a further gain. Our experiments show that the encodings of PB(AMO) constraints can be substantially smaller than those of PB constraints. PB(AMO) encodings allow many more instances to be solved within a time limit, and solving time is improved by more than one order of magnitude in some cases. We also observed that there is no single overall winner among the considered encodings, but efficiency of each encoding may depend on PB(AMO) characteristics such as the magnitude of coefficient values.

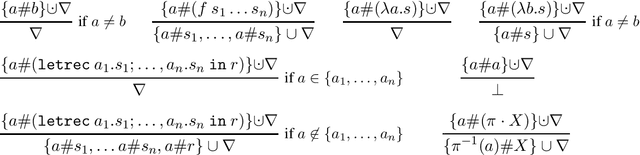
Nominal Unification and Matching of Higher Order Expressions with Recursive Let

A sound and complete algorithm for nominal unification of higher-order expressions with a recursive let is described, and shown to run in nondeterministic polynomial time. We also explore specializations like nominal letrec-matching for expressions, for DAGs, and for garbage-free expressions and determine their complexity. Finally, we also provide a nominal unification algorithm for higher-order expressions with recursive let and atom-variables, where we show that it also runs in nondeterministic polynomial time.