A Preliminary Case Study of Planning With Complex Transitions: Plotting

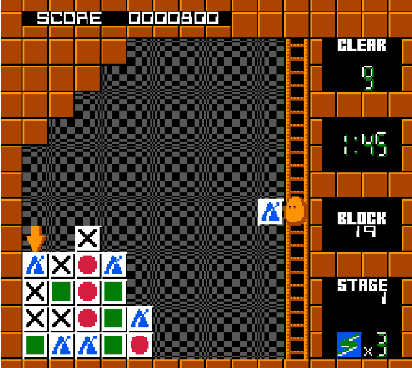
Plotting is a tile-matching puzzle video game published by Taito in 1989. Its objective is to reduce a given grid of coloured blocks down to a goal number or fewer. This is achieved by the avatar character repeatedly shooting the block it holds into the grid. Plotting is an example of a planning problem: given a model of the environment, a planning problem asks us to find a sequence of actions that can lead from an initial state of the environment to a given goal state while respecting some constraints. The key difficulty in modelling Plotting is in capturing the way the puzzle state changes after each shot. A single shot can affect multiple tiles directly, and the grid is affected by gravity so numerous other tiles can be affected indirectly. We present and evaluate a constraint model of the Plotting problem that captures this complexity. We also discuss the difficulties and inefficiencies of modelling Plotting in PDDL, the standard language used for input to specialised AI planners. We conclude by arguing that AI planning could benefit from a richer modelling language.

SAT Encodings for Pseudo-Boolean Constraints Together With At-Most-One Constraints

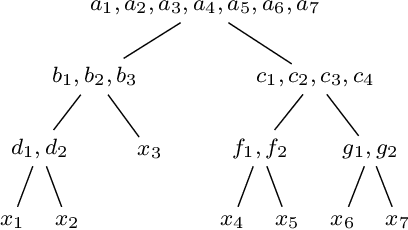
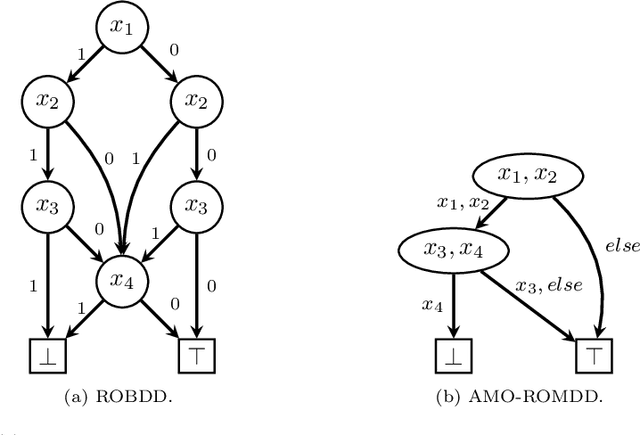
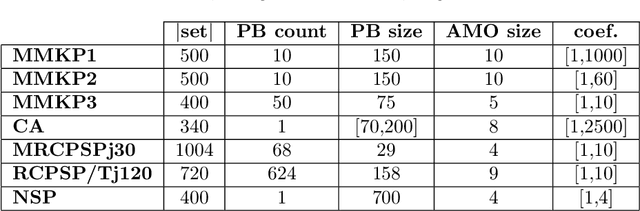
When solving a combinatorial problem using propositional satisfiability (SAT), the encoding of the problem is of vital importance. We study encodings of Pseudo-Boolean (PB) constraints, a common type of arithmetic constraint that appears in a wide variety of combinatorial problems such as timetabling, scheduling, and resource allocation. In some cases PB constraints occur together with at-most-one (AMO) constraints over subsets of their variables (forming PB(AMO) constraints). Recent work has shown that taking account of AMOs when encoding PB constraints using decision diagrams can produce a dramatic improvement in solver efficiency. In this paper we extend the approach to other state-of-the-art encodings of PB constraints, developing several new encodings for PB(AMO) constraints. Also, we present a more compact and efficient version of the popular Generalized Totalizer encoding, named Reduced Generalized Totalizer. This new encoding is also adapted for PB(AMO) constraints for a further gain. Our experiments show that the encodings of PB(AMO) constraints can be substantially smaller than those of PB constraints. PB(AMO) encodings allow many more instances to be solved within a time limit, and solving time is improved by more than one order of magnitude in some cases. We also observed that there is no single overall winner among the considered encodings, but efficiency of each encoding may depend on PB(AMO) characteristics such as the magnitude of coefficient values.