On Grid Graph Reachability and Puzzle Games

Many puzzle video games, like Sokoban, involve moving some agent in a maze. The reachable locations are usually apparent for a human player, and the difficulty of the game is mainly related to performing actions on objects, such as pushing (reachable) boxes. For this reason, the difficulty of a particular level is often measured as the number of actions on objects, other than agent walking, needed to find a solution. In this paper we study CP and SAT approaches for solving these kind of problems. We review some reachability encodings and propose a new one. We empirically show that the new encoding is well-suited for solving puzzle problems in the planning as SAT paradigm, especially when considering the execution of several actions in parallel.

A Good Snowman is Hard to Plan

In this work we face a challenging puzzle video game: A Good Snowman is Hard to Build. The objective of the game is to build snowmen by moving and stacking snowballs on a discrete grid. For the sake of player engagement with the game, it is interesting to avoid that a player finds a much easier solution than the one the designer expected. Therefore, having tools that are able to certify the optimality of solutions is crucial. Although the game can be stated as a planning problem and can be naturally modelled in PDDL, we show that a direct translation to SAT clearly outperforms off-the-shelf state-of-the-art planners. As we show, this is mainly due to the fact that reachability properties can be easily modelled in SAT, allowing for shorter plans, whereas using axioms to express a reachability derived predicate in PDDL does not result in any significant reduction of solving time with the considered planners. We deal with a set of 51 levels, both original and crafted, solving 43 and with 8 challenging instances still remaining to be solved.

SAT Encodings for Pseudo-Boolean Constraints Together With At-Most-One Constraints

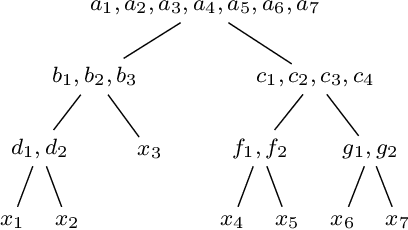
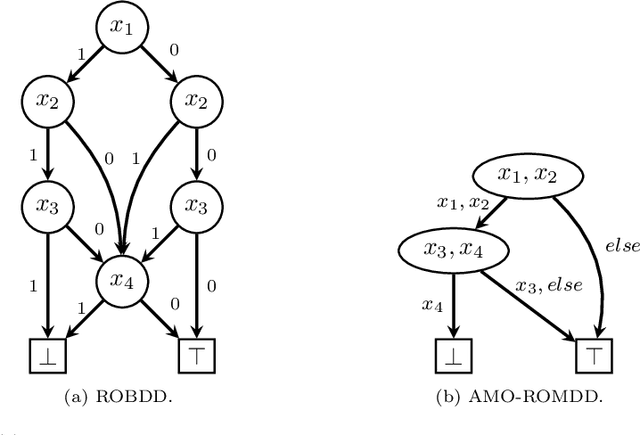
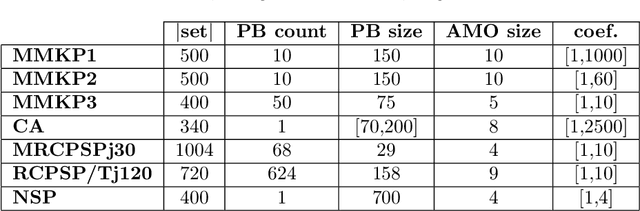
When solving a combinatorial problem using propositional satisfiability (SAT), the encoding of the problem is of vital importance. We study encodings of Pseudo-Boolean (PB) constraints, a common type of arithmetic constraint that appears in a wide variety of combinatorial problems such as timetabling, scheduling, and resource allocation. In some cases PB constraints occur together with at-most-one (AMO) constraints over subsets of their variables (forming PB(AMO) constraints). Recent work has shown that taking account of AMOs when encoding PB constraints using decision diagrams can produce a dramatic improvement in solver efficiency. In this paper we extend the approach to other state-of-the-art encodings of PB constraints, developing several new encodings for PB(AMO) constraints. Also, we present a more compact and efficient version of the popular Generalized Totalizer encoding, named Reduced Generalized Totalizer. This new encoding is also adapted for PB(AMO) constraints for a further gain. Our experiments show that the encodings of PB(AMO) constraints can be substantially smaller than those of PB constraints. PB(AMO) encodings allow many more instances to be solved within a time limit, and solving time is improved by more than one order of magnitude in some cases. We also observed that there is no single overall winner among the considered encodings, but efficiency of each encoding may depend on PB(AMO) characteristics such as the magnitude of coefficient values.

Solving the Wastewater Treatment Plant Problem with SMT

In this paper we introduce the Wastewater Treatment Plant Problem, a real-world scheduling problem, and compare the performance of several tools on it. We show that, for a naive modeling, state-of-the-art SMT solvers outperform other tools ranging from mathematical programming to constraint programming. We use both real and randomly generated benchmarks. From this and similar results, we claim for the convenience of developing compiler front-ends being able to translate from constraint programming languages to the SMT-LIB standard language.