Athanor: Local Search over Abstract Constraint Specifications

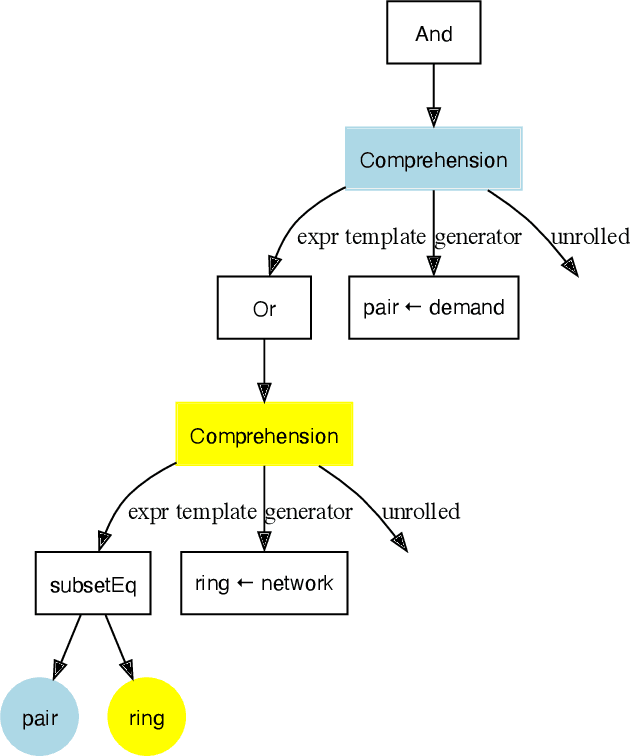
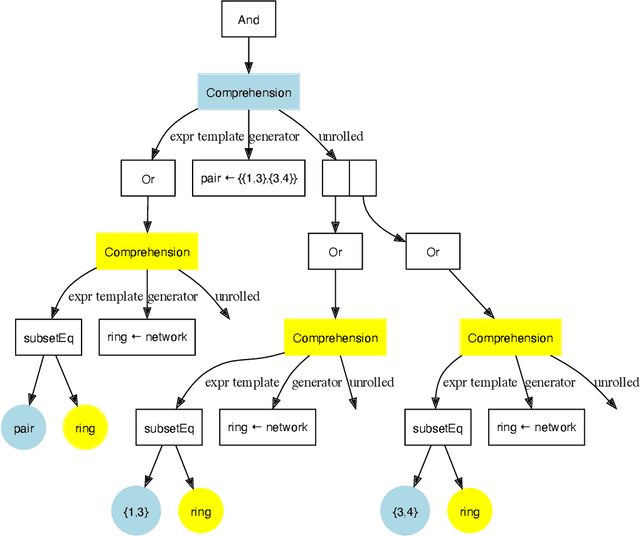
Local search is a common method for solving combinatorial optimisation problems. We focus on general-purpose local search solvers that accept as input a constraint model - a declarative description of a problem consisting of a set of decision variables under a set of constraints. Existing approaches typically take as input models written in solver-independent constraint modelling languages like MiniZinc. The Athanor solver we describe herein differs in that it begins from a specification of a problem in the abstract constraint specification language Essence, which allows problems to be described without commitment to low-level modelling decisions through its support for a rich set of abstract types. The advantage of proceeding from Essence is that the structure apparent in a concise, abstract specification of a problem can be exploited to generate high quality neighbourhoods automatically, avoiding the difficult task of identifying that structure in an equivalent constraint model. Based on the twin benefits of neighbourhoods derived from high level types and the scalability derived by searching directly over those types, our empirical results demonstrate strong performance in practice relative to existing solution methods.

Towards a Model of Puzznic

We report on progress in modelling and solving Puzznic, a video game requiring the player to plan sequences of moves to clear a grid by matching blocks. We focus here on levels with no moving blocks. We compare a planning approach and three constraint programming approaches on a small set of benchmark instances. The planning approach is at present superior to the constraint programming approaches, but we outline proposals for improving the constraint models.

Challenges in Modelling and Solving Plotting with PDDL

We study a planning problem based on Plotting, a tile-matching puzzle video game published by Taito in 1989. The objective of this game is to remove a target number of coloured blocks from a grid by sequentially shooting blocks into the grid. Plotting features complex transitions after every shot: various blocks are affected directly, while others can be indirectly affected by gravity. We highlight the challenges of modelling Plotting with PDDL and of solving it with a grounding-based state-of-the-art planner.

Learning to Select SAT Encodings for Pseudo-Boolean and Linear Integer Constraints

Many constraint satisfaction and optimisation problems can be solved effectively by encoding them as instances of the Boolean Satisfiability problem (SAT). However, even the simplest types of constraints have many encodings in the literature with widely varying performance, and the problem of selecting suitable encodings for a given problem instance is not trivial. We explore the problem of selecting encodings for pseudo-Boolean and linear constraints using a supervised machine learning approach. We show that it is possible to select encodings effectively using a standard set of features for constraint problems; however we obtain better performance with a new set of features specifically designed for the pseudo-Boolean and linear constraints. In fact, we achieve good results when selecting encodings for unseen problem classes. Our results compare favourably to AutoFolio when using the same feature set. We discuss the relative importance of instance features to the task of selecting the best encodings, and compare several variations of the machine learning method.

A Framework for Generating Informative Benchmark Instances

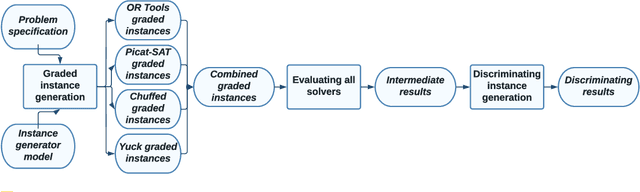
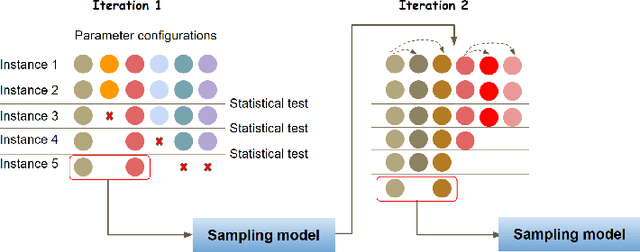
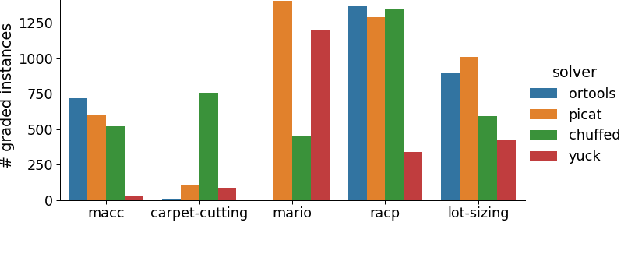
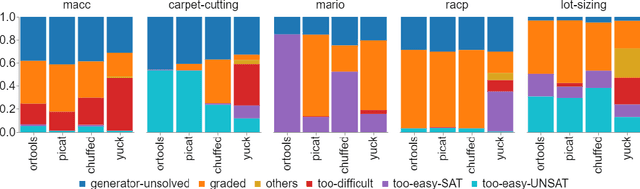
Benchmarking is an important tool for assessing the relative performance of alternative solving approaches. However, the utility of benchmarking is limited by the quantity and quality of the available problem instances. Modern constraint programming languages typically allow the specification of a class-level model that is parameterised over instance data. This separation presents an opportunity for automated approaches to generate instance data that define instances that are graded (solvable at a certain difficulty level for a solver) or can discriminate between two solving approaches. In this paper, we introduce a framework that combines these two properties to generate a large number of benchmark instances, purposely generated for effective and informative benchmarking. We use five problems that were used in the MiniZinc competition to demonstrate the usage of our framework. In addition to producing a ranking among solvers, our framework gives a broader understanding of the behaviour of each solver for the whole instance space; for example by finding subsets of instances where the solver performance significantly varies from its average performance.

Automatic Tabulation in Constraint Models

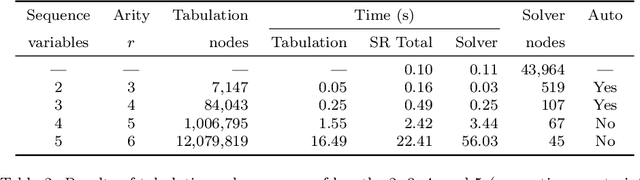
The performance of a constraint model can often be improved by converting a subproblem into a single table constraint. In this paper we study heuristics for identifying promising candidate subproblems, where converting the candidate into a table constraint is likely to improve solver performance. We propose a small set of heuristics to identify common cases, such as expressions that will propagate weakly. The process of discovering promising subproblems and tabulating them is entirely automated in the constraint modelling tool Savile Row. Caches are implemented to avoid tabulating equivalent subproblems many times. We give a simple algorithm to generate table constraints directly from a constraint expression in \savilerow. We demonstrate good performance on the benchmark problems used in earlier work on tabulation, and also for several new problem classes. In some cases, the entirely automated process leads to orders of magnitude improvements in solver performance.

Towards Reformulating Essence Specifications for Robustness

The Essence language allows a user to specify a constraint problem at a level of abstraction above that at which constraint modelling decisions are made. Essence specifications are refined into constraint models using the Conjure automated modelling tool, which employs a suite of refinement rules. However, Essence is a rich language in which there are many equivalent ways to specify a given problem. A user may therefore omit the use of domain attributes or abstract types, resulting in fewer refinement rules being applicable and therefore a reduced set of output models from which to select. This paper addresses the problem of recovering this information automatically to increase the robustness of the quality of the output constraint models in the face of variation in the input Essence specification. We present reformulation rules that can change the type of a decision variable or add attributes that shrink its domain. We demonstrate the efficacy of this approach in terms of the quantity and quality of models Conjure can produce from the transformed specification compared with the original.

SAT Encodings for Pseudo-Boolean Constraints Together With At-Most-One Constraints

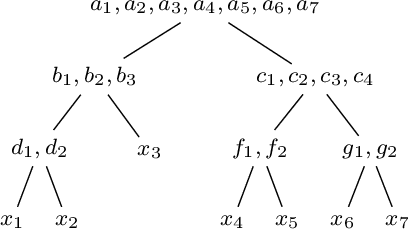
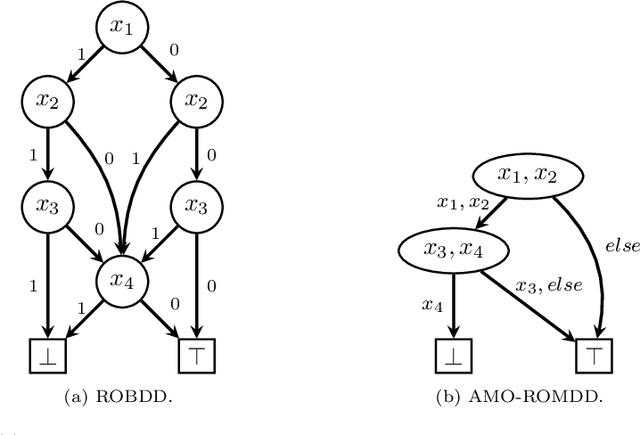
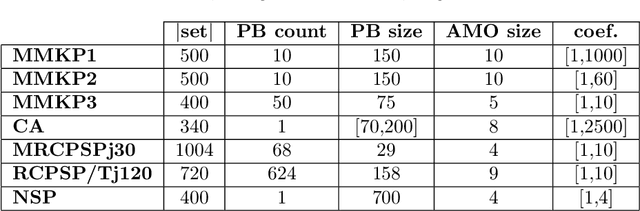
When solving a combinatorial problem using propositional satisfiability (SAT), the encoding of the problem is of vital importance. We study encodings of Pseudo-Boolean (PB) constraints, a common type of arithmetic constraint that appears in a wide variety of combinatorial problems such as timetabling, scheduling, and resource allocation. In some cases PB constraints occur together with at-most-one (AMO) constraints over subsets of their variables (forming PB(AMO) constraints). Recent work has shown that taking account of AMOs when encoding PB constraints using decision diagrams can produce a dramatic improvement in solver efficiency. In this paper we extend the approach to other state-of-the-art encodings of PB constraints, developing several new encodings for PB(AMO) constraints. Also, we present a more compact and efficient version of the popular Generalized Totalizer encoding, named Reduced Generalized Totalizer. This new encoding is also adapted for PB(AMO) constraints for a further gain. Our experiments show that the encodings of PB(AMO) constraints can be substantially smaller than those of PB constraints. PB(AMO) encodings allow many more instances to be solved within a time limit, and solving time is improved by more than one order of magnitude in some cases. We also observed that there is no single overall winner among the considered encodings, but efficiency of each encoding may depend on PB(AMO) characteristics such as the magnitude of coefficient values.

A Review of Literature on Parallel Constraint Solving

As multicore computing is now standard, it seems irresponsible for constraints researchers to ignore the implications of it. Researchers need to address a number of issues to exploit parallelism, such as: investigating which constraint algorithms are amenable to parallelisation; whether to use shared memory or distributed computation; whether to use static or dynamic decomposition; and how to best exploit portfolios and cooperating search. We review the literature, and see that we can sometimes do quite well, some of the time, on some instances, but we are far from a general solution. Yet there seems to be little overall guidance that can be given on how best to exploit multicore computers to speed up constraint solving. We hope at least that this survey will provide useful pointers to future researchers wishing to correct this situation. Under consideration in Theory and Practice of Logic Programming (TPLP).

Generalized Support and Formal Development of Constraint Propagators

Constraint programming is a family of techniques for solving combinatorial problems, where the problem is modelled as a set of decision variables (typically with finite domains) and a set of constraints that express relations among the decision variables. One key concept in constraint programming is propagation: reasoning on a constraint or set of constraints to derive new facts, typically to remove values from the domains of decision variables. Specialised propagation algorithms (propagators) exist for many classes of constraints. The concept of support is pervasive in the design of propagators. Traditionally, when a domain value ceases to have support, it may be removed because it takes part in no solutions. Arc-consistency algorithms such as AC2001 make use of support in the form of a single domain value. GAC algorithms such as GAC-Schema use a tuple of values to support each literal. We generalize these notions of support in two ways. First, we allow a set of tuples to act as support. Second, the supported object is generalized from a set of literals (GAC-Schema) to an entire constraint or any part of it. We design a methodology for developing correct propagators using generalized support. A constraint is expressed as a family of support properties, which may be proven correct against the formal semantics of the constraint. Using Curry-Howard isomorphism to interpret constructive proofs as programs, we show how to derive correct propagators from the constructive proofs of the support properties. The framework is carefully designed to allow efficient algorithms to be produced. Derived algorithms may make use of dynamic literal triggers or watched literals for efficiency. Finally, two case studies of deriving efficient algorithms are given.