A General Framework for Stable Roommates Problems using Answer Set Programming

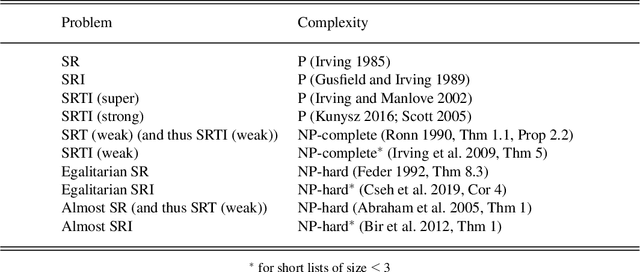
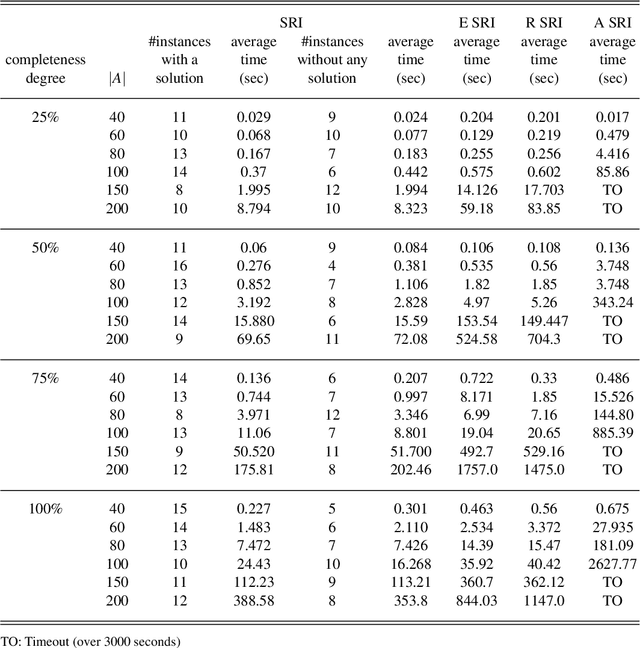
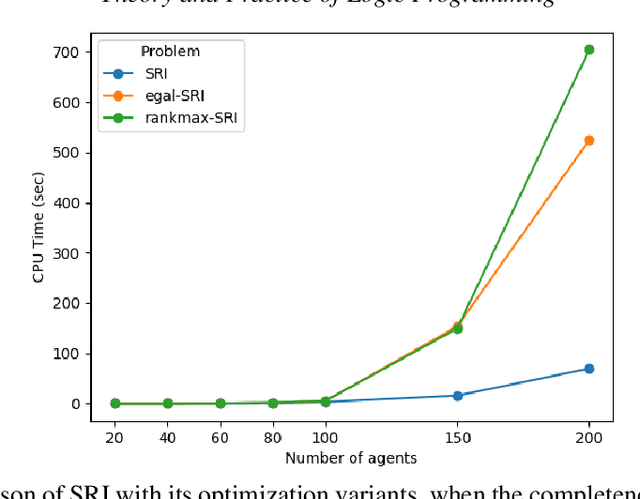
The Stable Roommates problem (SR) is characterized by the preferences of agents over other agents as roommates: each agent ranks all others in strict order of preference. A solution to SR is then a partition of the agents into pairs so that each pair shares a room, and there is no pair of agents that would block this matching (i.e., who prefers the other to their roommate in the matching). There are interesting variations of SR that are motivated by applications (e.g., the preference lists may be incomplete (SRI) and involve ties (SRTI)), and that try to find a more fair solution (e.g., Egalitarian SR). Unlike the Stable Marriage problem, every SR instance is not guaranteed to have a solution. For that reason, there are also variations of SR that try to find a good-enough solution (e.g., Almost SR). Most of these variations are NP-hard. We introduce a formal framework, called SRTI-ASP, utilizing the logic programming paradigm Answer Set Programming, that is provable and general enough to solve many of such variations of SR. Our empirical analysis shows that SRTI-ASP is also promising for applications. This paper is under consideration for acceptance in TPLP.

A Review of Literature on Parallel Constraint Solving

As multicore computing is now standard, it seems irresponsible for constraints researchers to ignore the implications of it. Researchers need to address a number of issues to exploit parallelism, such as: investigating which constraint algorithms are amenable to parallelisation; whether to use shared memory or distributed computation; whether to use static or dynamic decomposition; and how to best exploit portfolios and cooperating search. We review the literature, and see that we can sometimes do quite well, some of the time, on some instances, but we are far from a general solution. Yet there seems to be little overall guidance that can be given on how best to exploit multicore computers to speed up constraint solving. We hope at least that this survey will provide useful pointers to future researchers wishing to correct this situation. Under consideration in Theory and Practice of Logic Programming (TPLP).

The Ultrametric Constraint and its Application to Phylogenetics

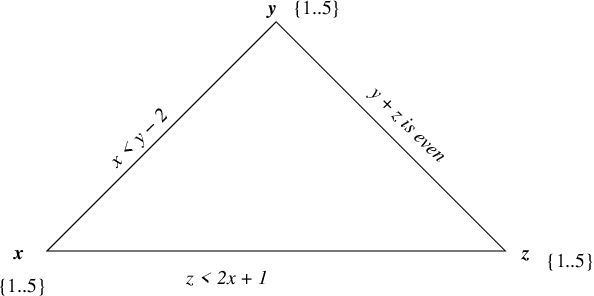
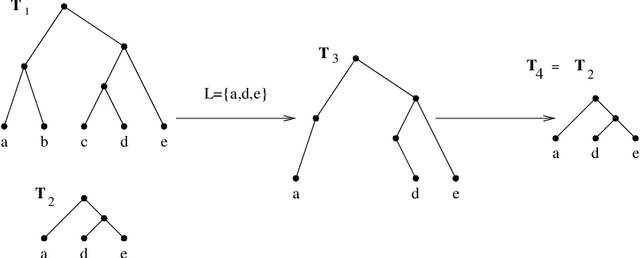
A phylogenetic tree shows the evolutionary relationships among species. Internal nodes of the tree represent speciation events and leaf nodes correspond to species. A goal of phylogenetics is to combine such trees into larger trees, called supertrees, whilst respecting the relationships in the original trees. A rooted tree exhibits an ultrametric property; that is, for any three leaves of the tree it must be that one pair has a deeper most recent common ancestor than the other pairs, or that all three have the same most recent common ancestor. This inspires a constraint programming encoding for rooted trees. We present an efficient constraint that enforces the ultrametric property over a symmetric array of constrained integer variables, with the inevitable property that the lower bounds of any three variables are mutually supportive. We show that this allows an efficient constraint-based solution to the supertree construction problem. We demonstrate that the versatility of constraint programming can be exploited to allow solutions to variants of the supertree construction problem.

An n-ary Constraint for the Stable Marriage Problem

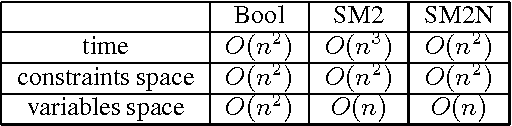
We present an n-ary constraint for the stable marriage problem. This constraint acts between two sets of integer variables where the domains of those variables represent preferences. Our constraint enforces stability and disallows bigamy. For a stable marriage instance with $n$ men and $n$ women we require only one of these constraints, and the complexity of enforcing arc-consistency is $O(n^2)$ which is optimal in the size of input. Our computational studies show that our n-ary constraint is significantly faster and more space efficient than the encodings presented in \cite{cp01}. We also introduce a new problem to the constraint community, the sex-equal stable marriage problem.