A General Framework for Dynamic MAPF using Multi-Shot ASP and Tunnels

MAPF problem aims to find plans for multiple agents in an environment within a given time, such that the agents do not collide with each other or obstacles. Motivated by the execution and monitoring of these plans, we study Dynamic MAPF (D-MAPF) problem, which allows changes such as agents entering/leaving the environment or obstacles being removed/moved. Considering the requirements of real-world applications in warehouses with the presence of humans, we introduce 1) a general definition for D-MAPF (applicable to variations of D-MAPF), 2) a new framework to solve D-MAPF (utilizing multi-shot computation, and allowing different methods to solve D-MAPF), and 3) a new ASP-based method to solve D-MAPF (combining advantages of replanning and repairing methods, with a novel concept of tunnels to specify where agents can move). We have illustrated the strengths and weaknesses of this method by experimental evaluations, from the perspectives of computational performance and quality of solutions.

Stable Marriage Problems with Ties and Incomplete Preferences: An Empirical Comparison of ASP, SAT, ILP, CP, and Local Search Methods

We study a variation of the Stable Marriage problem, where every man and every woman express their preferences as preference lists which may be incomplete and contain ties. This problem is called the Stable Marriage problem with Ties and Incomplete preferences (SMTI). We consider three optimization variants of SMTI, Max Cardinality, Sex-Equal and Egalitarian, and empirically compare the following methods to solve them: Answer Set Programming, Constraint Programming, Integer Linear Programming. For Max Cardinality, we compare these methods with Local Search methods as well. We also empirically compare Answer Set Programming with Propositional Satisfiability, for SMTI instances. This paper is under consideration for acceptance in Theory and Practice of Logic Programming (TPLP).

Knowledge-Based Stable Roommates Problem: A Real-World Application

The Stable Roommates problem with Ties and Incomplete lists (SRTI) is a matching problem characterized by the preferences of agents over other agents as roommates, where the preferences may have ties or be incomplete. SRTI asks for a matching that is stable and, sometimes, optimizes a domain-independent fairness criterion (e.g., Egalitarian). However, in real-world applications (e.g., assigning students as roommates at a dormitory), we usually consider a variety of domain-specific criteria depending on preferences over the habits and desires of the agents. With this motivation, we introduce a knowledge-based method to SRTI considering domain-specific knowledge, and investigate its real-world application for assigning students as roommates at a university dormitory. This paper is under consideration for acceptance in Theory and Practice of Logic Programming (TPLP).

Dynamic Multi-Agent Path Finding based on Conflict Resolution using Answer Set Programming

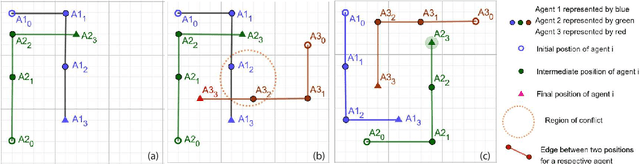
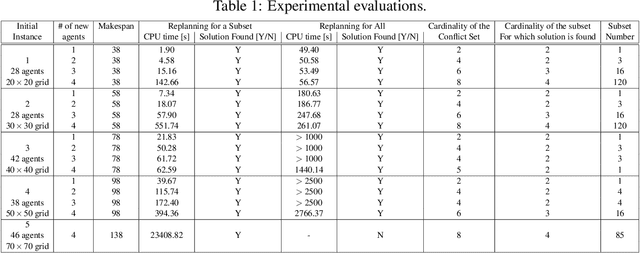
We study a dynamic version of multi-agent path finding problem (called D-MAPF) where existing agents may leave and new agents may join the team at different times. We introduce a new method to solve D-MAPF based on conflict-resolution. The idea is, when a set of new agents joins the team and there are conflicts, instead of replanning for the whole team, to replan only for a minimal subset of agents whose plans conflict with each other. We utilize answer set programming as part of our method for planning, replanning and identifying minimal set of conflicts.

Solving Gossip Problems using Answer Set Programming: An Epistemic Planning Approach

We investigate the use of Answer Set Programming to solve variations of gossip problems, by modeling them as epistemic planning problems.

Reasoning about Cardinal Directions between 3-Dimensional Extended Objects using Answer Set Programming

We propose a novel formal framework (called 3D-nCDC-ASP) to represent and reason about cardinal directions between extended objects in 3-dimensional (3D) space, using Answer Set Programming (ASP). 3D-nCDC-ASP extends Cardinal Directional Calculus (CDC) with a new type of default constraints, and nCDC-ASP to 3D. 3D-nCDC-ASP provides a flexible platform offering different types of reasoning: Nonmonotonic reasoning with defaults, checking consistency of a set of constraints on 3D cardinal directions between objects, explaining inconsistencies, and inferring missing CDC relations. We prove the soundness of 3D-nCDC-ASP, and illustrate its usefulness with applications. This paper is under consideration for acceptance in TPLP.

Explanation Generation for Multi-Modal Multi-Agent Path Finding with Optimal Resource Utilization using Answer Set Programming

The multi-agent path finding (MAPF) problem is a combinatorial search problem that aims at finding paths for multiple agents (e.g., robots) in an environment (e.g., an autonomous warehouse) such that no two agents collide with each other, and subject to some constraints on the lengths of paths. We consider a general version of MAPF, called mMAPF, that involves multi-modal transportation modes (e.g., due to velocity constraints) and consumption of different types of resources (e.g., batteries). The real-world applications of mMAPF require flexibility (e.g., solving variations of mMAPF) as well as explainability. Our earlier studies on mMAPF have focused on the former challenge of flexibility. In this study, we focus on the latter challenge of explainability, and introduce a method for generating explanations for queries regarding the feasibility and optimality of solutions, the nonexistence of solutions, and the observations about solutions. Our method is based on answer set programming. This paper is under consideration for acceptance in TPLP.

Human Robot Collaborative Assembly Planning: An Answer Set Programming Approach

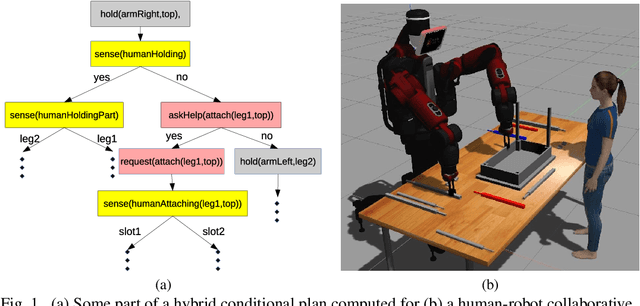
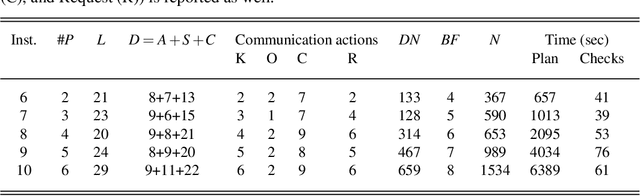
For planning an assembly of a product from a given set of parts, robots necessitate certain cognitive skills: high-level planning is needed to decide the order of actuation actions, while geometric reasoning is needed to check the feasibility of these actions. For collaborative assembly tasks with humans, robots require further cognitive capabilities, such as commonsense reasoning, sensing, and communication skills, not only to cope with the uncertainty caused by incomplete knowledge about the humans' behaviors but also to ensure safer collaborations. We propose a novel method for collaborative assembly planning under uncertainty, that utilizes hybrid conditional planning extended with commonsense reasoning and a rich set of communication actions for collaborative tasks. Our method is based on answer set programming. We show the applicability of our approach in a real-world assembly domain, where a bi-manual Baxter robot collaborates with a human teammate to assemble furniture. This manuscript is under consideration for acceptance in TPLP.

A General Framework for Stable Roommates Problems using Answer Set Programming

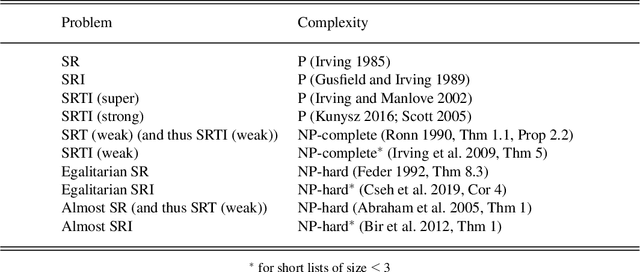
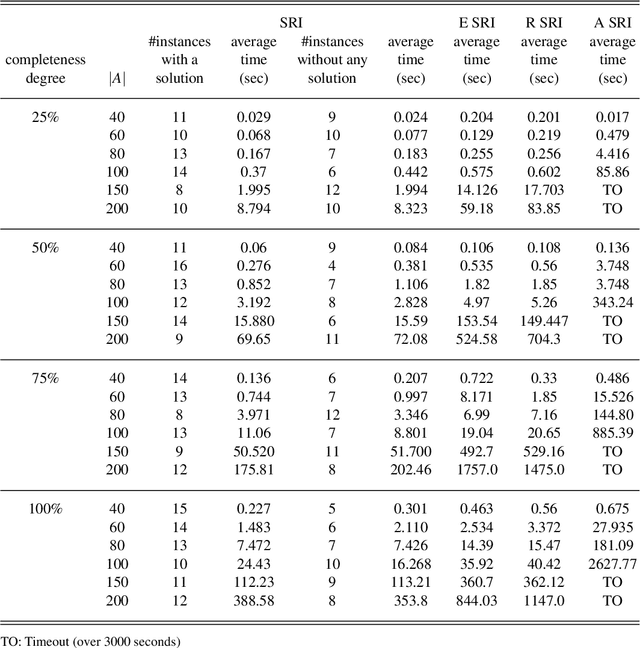
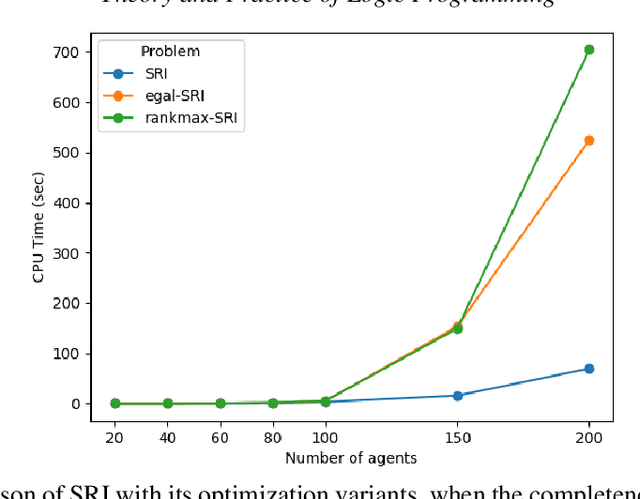
The Stable Roommates problem (SR) is characterized by the preferences of agents over other agents as roommates: each agent ranks all others in strict order of preference. A solution to SR is then a partition of the agents into pairs so that each pair shares a room, and there is no pair of agents that would block this matching (i.e., who prefers the other to their roommate in the matching). There are interesting variations of SR that are motivated by applications (e.g., the preference lists may be incomplete (SRI) and involve ties (SRTI)), and that try to find a more fair solution (e.g., Egalitarian SR). Unlike the Stable Marriage problem, every SR instance is not guaranteed to have a solution. For that reason, there are also variations of SR that try to find a good-enough solution (e.g., Almost SR). Most of these variations are NP-hard. We introduce a formal framework, called SRTI-ASP, utilizing the logic programming paradigm Answer Set Programming, that is provable and general enough to solve many of such variations of SR. Our empirical analysis shows that SRTI-ASP is also promising for applications. This paper is under consideration for acceptance in TPLP.

Proceedings 35th International Conference on Logic Programming (Technical Communications)

Since the first conference held in Marseille in 1982, ICLP has been the premier international event for presenting research in logic programming. Contributions are sought in all areas of logic programming, including but not restricted to: Foundations: Semantics, Formalisms, Nonmonotonic reasoning, Knowledge representation. Languages: Concurrency, Objects, Coordination, Mobility, Higher Order, Types, Modes, Assertions, Modules, Meta-programming, Logic-based domain-specific languages, Programming Techniques. Declarative programming: Declarative program development, Analysis, Type and mode inference, Partial evaluation, Abstract interpretation, Transformation, Validation, Verification, Debugging, Profiling, Testing, Execution visualization Implementation: Virtual machines, Compilation, Memory management, Parallel/distributed execution, Constraint handling rules, Tabling, Foreign interfaces, User interfaces. Related Paradigms and Synergies: Inductive and Co-inductive Logic Programming, Constraint Logic Programming, Answer Set Programming, Interaction with SAT, SMT and CSP solvers, Logic programming techniques for type inference and theorem proving, Argumentation, Probabilistic Logic Programming, Relations to object-oriented and Functional programming. Applications: Databases, Big Data, Data integration and federation, Software engineering, Natural language processing, Web and Semantic Web, Agents, Artificial intelligence, Computational life sciences, Education, Cybersecurity, and Robotics.