David Manlove
Couples can be tractable: New algorithms and hardness results for the Hospitals / Residents problem with Couples
Nov 01, 2023Abstract:In this paper we study the {\sc Hospitals / Residents problem with Couples} ({\sc hrc}), where a solution is a stable matching or a report that none exists. We present a novel polynomial-time algorithm that can find a near-feasible stable matching (adjusting the hospitals' capacities by at most 1) in an {\sc hrc} instance where the couples' preferences are sub-responsive (i.e., if one member switches to a better hospital, than the couple also improves) and sub-complete (i.e., each pair of hospitals that are individually acceptable to both members are jointly acceptable for the couple) by reducing it to an instance of the {\sc Stable Fixtures} problem. We also present a polynomial-time algorithm for {\sc hrc} in a sub-responsive, sub-complete instance that is a Dual Market, or where all couples are one of several possible types. We show that our algorithm also implies the polynomial-time solvability of a stable b-matching problem, where the underlying graph is a multigraph with loops. We complement our algorithms with several hardness results. We show that {\sc hrc} with sub-responsive and sub-complete couples is NP-hard, even with other strong restrictions. We also show that {\sc hrc} with a Dual Market is NP-hard under several simultaneous restrictions. Finally, we show that the problem of finding a matching with the minimum number of blocking pairs in {\sc hrc} is not approximable within $m^{1-\varepsilon}$, for any $\varepsilon>0$, where $m$ is the total length of the hospitals' preference lists, unless P=NP, even if each couple applies to only one pair of hospitals. Our polynomial-time solvability results greatly expand the class of known tractable instances of {\sc hrc} and provide additional evidence as to why long-standing entry-level labour markets that allow couples such as the National Resident Matching Program remain successful to this day.
A General Framework for Stable Roommates Problems using Answer Set Programming
Aug 07, 2020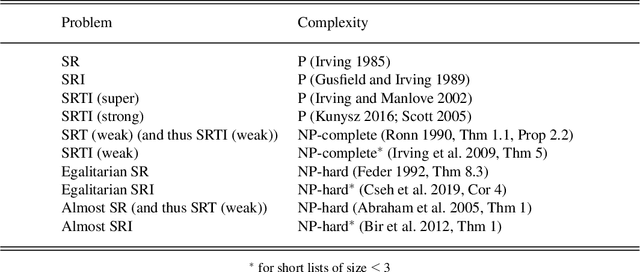

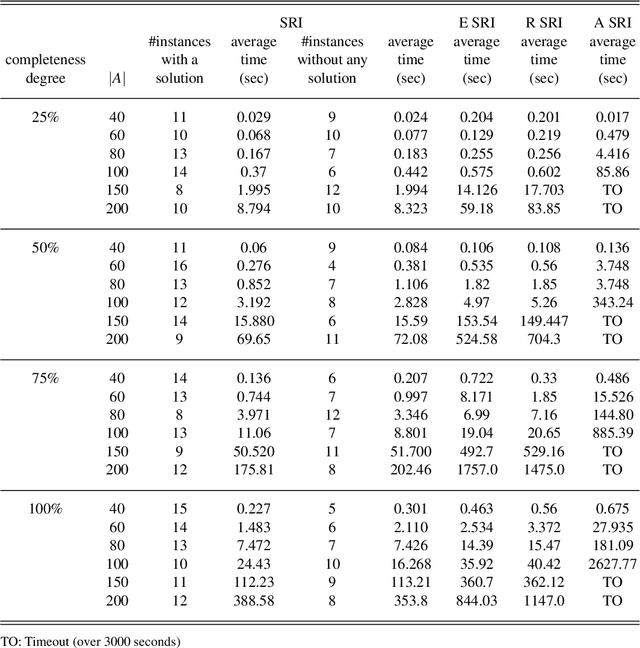
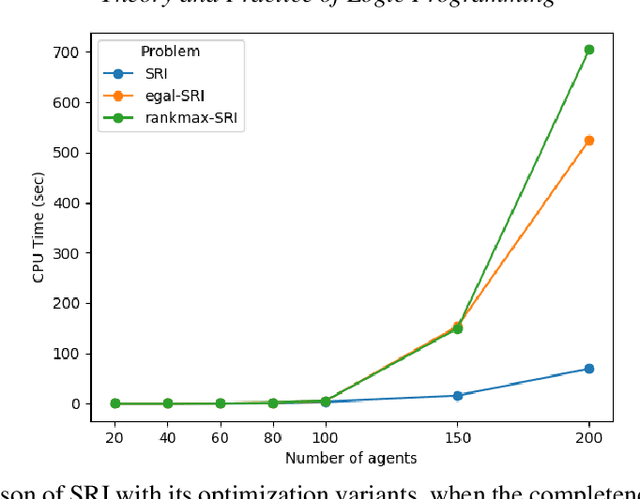
Abstract:The Stable Roommates problem (SR) is characterized by the preferences of agents over other agents as roommates: each agent ranks all others in strict order of preference. A solution to SR is then a partition of the agents into pairs so that each pair shares a room, and there is no pair of agents that would block this matching (i.e., who prefers the other to their roommate in the matching). There are interesting variations of SR that are motivated by applications (e.g., the preference lists may be incomplete (SRI) and involve ties (SRTI)), and that try to find a more fair solution (e.g., Egalitarian SR). Unlike the Stable Marriage problem, every SR instance is not guaranteed to have a solution. For that reason, there are also variations of SR that try to find a good-enough solution (e.g., Almost SR). Most of these variations are NP-hard. We introduce a formal framework, called SRTI-ASP, utilizing the logic programming paradigm Answer Set Programming, that is provable and general enough to solve many of such variations of SR. Our empirical analysis shows that SRTI-ASP is also promising for applications. This paper is under consideration for acceptance in TPLP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge