James Trimble
Couples can be tractable: New algorithms and hardness results for the Hospitals / Residents problem with Couples
Nov 01, 2023Abstract:In this paper we study the {\sc Hospitals / Residents problem with Couples} ({\sc hrc}), where a solution is a stable matching or a report that none exists. We present a novel polynomial-time algorithm that can find a near-feasible stable matching (adjusting the hospitals' capacities by at most 1) in an {\sc hrc} instance where the couples' preferences are sub-responsive (i.e., if one member switches to a better hospital, than the couple also improves) and sub-complete (i.e., each pair of hospitals that are individually acceptable to both members are jointly acceptable for the couple) by reducing it to an instance of the {\sc Stable Fixtures} problem. We also present a polynomial-time algorithm for {\sc hrc} in a sub-responsive, sub-complete instance that is a Dual Market, or where all couples are one of several possible types. We show that our algorithm also implies the polynomial-time solvability of a stable b-matching problem, where the underlying graph is a multigraph with loops. We complement our algorithms with several hardness results. We show that {\sc hrc} with sub-responsive and sub-complete couples is NP-hard, even with other strong restrictions. We also show that {\sc hrc} with a Dual Market is NP-hard under several simultaneous restrictions. Finally, we show that the problem of finding a matching with the minimum number of blocking pairs in {\sc hrc} is not approximable within $m^{1-\varepsilon}$, for any $\varepsilon>0$, where $m$ is the total length of the hospitals' preference lists, unless P=NP, even if each couple applies to only one pair of hospitals. Our polynomial-time solvability results greatly expand the class of known tractable instances of {\sc hrc} and provide additional evidence as to why long-standing entry-level labour markets that allow couples such as the National Resident Matching Program remain successful to this day.
Position-Indexed Formulations for Kidney Exchange
Jun 10, 2016

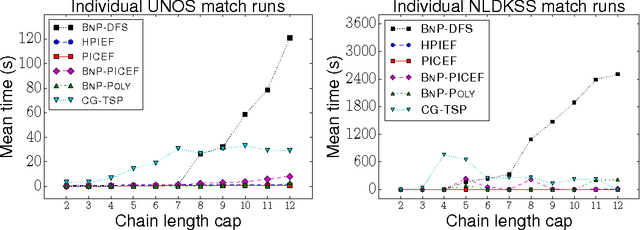
Abstract:A kidney exchange is an organized barter market where patients in need of a kidney swap willing but incompatible donors. Determining an optimal set of exchanges is theoretically and empirically hard. Traditionally, exchanges took place in cycles, with each participating patient-donor pair both giving and receiving a kidney. The recent introduction of chains, where a donor without a paired patient triggers a sequence of donations without requiring a kidney in return, increased the efficacy of fielded kidney exchanges---while also dramatically raising the empirical computational hardness of clearing the market in practice. While chains can be quite long, unbounded-length chains are not desirable: planned donations can fail before transplant for a variety of reasons, and the failure of a single donation causes the rest of that chain to fail, so parallel shorter chains are better in practice. In this paper, we address the tractable clearing of kidney exchanges with short cycles and chains that are long but bounded. This corresponds to the practice at most modern fielded kidney exchanges. We introduce three new integer programming formulations, two of which are compact. Furthermore, one of these models has a linear programming relaxation that is exactly as tight as the previous tightest formulation (which was not compact) for instances in which each donor has a paired patient. On real data from the UNOS nationwide exchange in the United States and the NLDKSS nationwide exchange in the United Kingdom, as well as on generated realistic large-scale data, we show that our new models are competitive with all existing solvers---in many cases outperforming all other solvers by orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge