Getting By Goal Misgeneralization With a Little Help From a Mentor

While reinforcement learning (RL) agents often perform well during training, they can struggle with distribution shift in real-world deployments. One particularly severe risk of distribution shift is goal misgeneralization, where the agent learns a proxy goal that coincides with the true goal during training but not during deployment. In this paper, we explore whether allowing an agent to ask for help from a supervisor in unfamiliar situations can mitigate this issue. We focus on agents trained with PPO in the CoinRun environment, a setting known to exhibit goal misgeneralization. We evaluate multiple methods for determining when the agent should request help and find that asking for help consistently improves performance. However, we also find that methods based on the agent's internal state fail to proactively request help, instead waiting until mistakes have already occurred. Further investigation suggests that the agent's internal state does not represent the coin at all, highlighting the importance of learning nuanced representations, the risks of ignoring everything not immediately relevant to reward, and the necessity of developing ask-for-help strategies tailored to the agent's training algorithm.

Softmax Probabilities (Mostly) Predict Large Language Model Correctness on Multiple-Choice Q&A

Although large language models (LLMs) perform impressively on many tasks, overconfidence remains a problem. We hypothesized that on multiple-choice Q&A tasks, wrong answers would be associated with smaller maximum softmax probabilities (MSPs) compared to correct answers. We comprehensively evaluate this hypothesis on ten open-source LLMs and five datasets, and find strong evidence for our hypothesis among models which perform well on the original Q&A task. For the six LLMs with the best Q&A performance, the AUROC derived from the MSP was better than random chance with p < 10^{-4} in 59/60 instances. Among those six LLMs, the average AUROC ranged from 60% to 69%. Leveraging these findings, we propose a multiple-choice Q&A task with an option to abstain and show that performance can be improved by selectively abstaining based on the MSP of the initial model response. We also run the same experiments with pre-softmax logits instead of softmax probabilities and find similar (but not identical) results.

Avoiding Catastrophe in Continuous Spaces by Asking for Help

Most reinforcement learning algorithms with formal regret guarantees assume all mistakes are reversible and rely on essentially trying all possible options. This approach leads to poor outcomes when some mistakes are irreparable or even catastrophic. We propose a variant of the contextual bandit problem where the goal is to minimize the chance of catastrophe. Specifically, we assume that the payoff each round represents the chance of avoiding catastrophe that round, and try to maximize the product of payoffs (the overall chance of avoiding catastrophe). To give the agent some chance of success, we allow a limited number of queries to a mentor and assume a Lipschitz continuous payoff function. We present an algorithm whose regret and rate of querying the mentor both approach 0 as the time horizon grows, assuming a continuous 1D state space and a relatively "simple" payoff function. We also provide a matching lower bound: without the simplicity assumption: any algorithm either constantly asks for help or is nearly guaranteed to cause catastrophe. Finally, we identify the key obstacle to generalizing our algorithm to a multi-dimensional state space.

Position-Indexed Formulations for Kidney Exchange

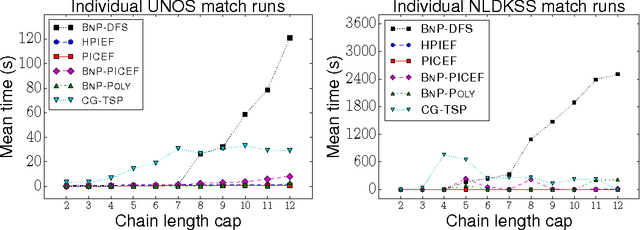
A kidney exchange is an organized barter market where patients in need of a kidney swap willing but incompatible donors. Determining an optimal set of exchanges is theoretically and empirically hard. Traditionally, exchanges took place in cycles, with each participating patient-donor pair both giving and receiving a kidney. The recent introduction of chains, where a donor without a paired patient triggers a sequence of donations without requiring a kidney in return, increased the efficacy of fielded kidney exchanges---while also dramatically raising the empirical computational hardness of clearing the market in practice. While chains can be quite long, unbounded-length chains are not desirable: planned donations can fail before transplant for a variety of reasons, and the failure of a single donation causes the rest of that chain to fail, so parallel shorter chains are better in practice. In this paper, we address the tractable clearing of kidney exchanges with short cycles and chains that are long but bounded. This corresponds to the practice at most modern fielded kidney exchanges. We introduce three new integer programming formulations, two of which are compact. Furthermore, one of these models has a linear programming relaxation that is exactly as tight as the previous tightest formulation (which was not compact) for instances in which each donor has a paired patient. On real data from the UNOS nationwide exchange in the United States and the NLDKSS nationwide exchange in the United Kingdom, as well as on generated realistic large-scale data, we show that our new models are competitive with all existing solvers---in many cases outperforming all other solvers by orders of magnitude.

Hardness of the Pricing Problem for Chains in Barter Exchanges

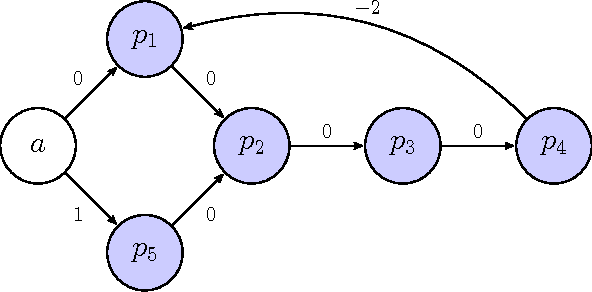
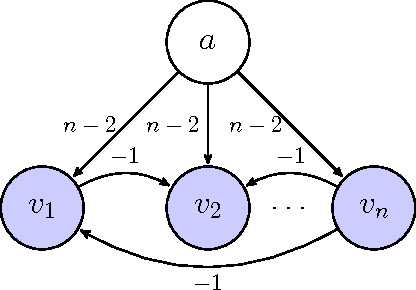
Kidney exchange is a barter market where patients trade willing but medically incompatible donors. These trades occur via cycles, where each patient-donor pair both gives and receives a kidney, and via chains, which begin with an altruistic donor who does not require a kidney in return. For logistical reasons, the maximum length of a cycle is typically limited to a small constant, while chains can be much longer. Given a compatibility graph of patient-donor pairs, altruists, and feasible potential transplants between them, finding even a maximum-cardinality set of vertex-disjoint cycles and chains is NP-hard. There has been much work on developing provably optimal solvers that are efficient in practice. One of the leading techniques has been branch and price, where column generation is used to incrementally bring cycles and chains into the optimization model on an as-needed basis. In particular, only positive-price columns need to be brought into the model. We prove that finding a positive-price chain is NP-complete. This shows incorrectness of two leading branch-and-price solvers that suggested polynomial-time chain pricing algorithms.