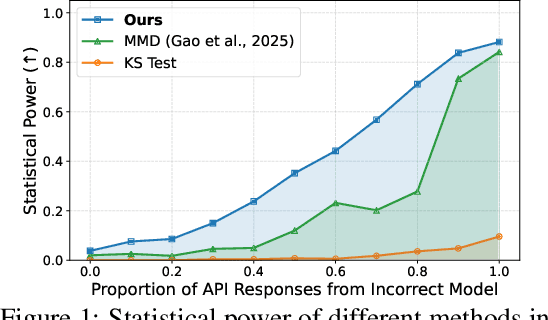
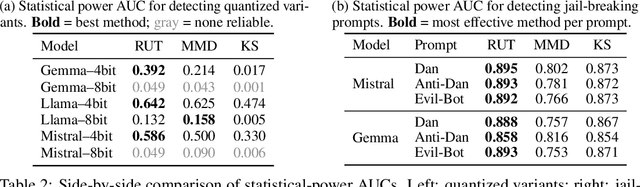
Auditing Black-Box LLM APIs with a Rank-Based Uniformity Test

As API access becomes a primary interface to large language models (LLMs), users often interact with black-box systems that offer little transparency into the deployed model. To reduce costs or maliciously alter model behaviors, API providers may discreetly serve quantized or fine-tuned variants, which can degrade performance and compromise safety. Detecting such substitutions is difficult, as users lack access to model weights and, in most cases, even output logits. To tackle this problem, we propose a rank-based uniformity test that can verify the behavioral equality of a black-box LLM to a locally deployed authentic model. Our method is accurate, query-efficient, and avoids detectable query patterns, making it robust to adversarial providers that reroute or mix responses upon the detection of testing attempts. We evaluate the approach across diverse threat scenarios, including quantization, harmful fine-tuning, jailbreak prompts, and full model substitution, showing that it consistently achieves superior statistical power over prior methods under constrained query budgets.

Reasoning by Superposition: A Theoretical Perspective on Chain of Continuous Thought

Large Language Models (LLMs) have demonstrated remarkable performance in many applications, including challenging reasoning problems via chain-of-thoughts (CoTs) techniques that generate ``thinking tokens'' before answering the questions. While existing theoretical works demonstrate that CoTs with discrete tokens boost the capability of LLMs, recent work on continuous CoTs lacks a theoretical understanding of why it outperforms discrete counterparts in various reasoning tasks such as directed graph reachability, a fundamental graph reasoning problem that includes many practical domain applications as special cases. In this paper, we prove that a two-layer transformer with $D$ steps of continuous CoTs can solve the directed graph reachability problem, where $D$ is the diameter of the graph, while the best known result of constant-depth transformers with discrete CoTs requires $O(n^2)$ decoding steps where $n$ is the number of vertices ($D<n$). In our construction, each continuous thought vector is a superposition state that encodes multiple search frontiers simultaneously (i.e., parallel breadth-first search (BFS)), while discrete CoTs must choose a single path sampled from the superposition state, which leads to sequential search that requires many more steps and may be trapped into local solutions. We also performed extensive experiments to verify that our theoretical construction aligns well with the empirical solution obtained via training dynamics. Notably, encoding of multiple search frontiers as a superposition state automatically emerges in training continuous CoTs, without explicit supervision to guide the model to explore multiple paths simultaneously.

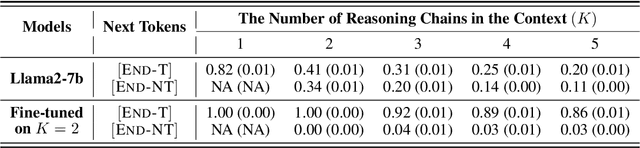
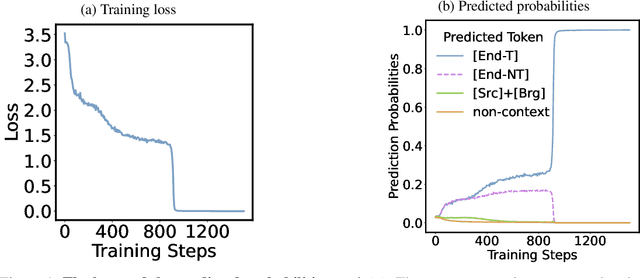
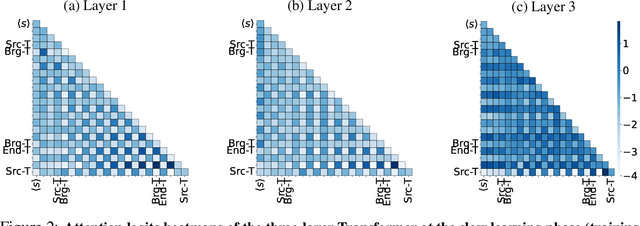
How Do LLMs Perform Two-Hop Reasoning in Context?

"Socrates is human. All humans are mortal. Therefore, Socrates is mortal." This classical example demonstrates two-hop reasoning, where a conclusion logically follows from two connected premises. While transformer-based Large Language Models (LLMs) can make two-hop reasoning, they tend to collapse to random guessing when faced with distracting premises. To understand the underlying mechanism, we train a three-layer transformer on synthetic two-hop reasoning tasks. The training dynamics show two stages: a slow learning phase, where the 3-layer transformer performs random guessing like LLMs, followed by an abrupt phase transitions, where the 3-layer transformer suddenly reaches $100%$ accuracy. Through reverse engineering, we explain the inner mechanisms for how models learn to randomly guess between distractions initially, and how they learn to ignore distractions eventually. We further propose a three-parameter model that supports the causal claims for the mechanisms to the training dynamics of the transformer. Finally, experiments on LLMs suggest that the discovered mechanisms generalize across scales. Our methodologies provide new perspectives for scientific understandings of LLMs and our findings provide new insights into how reasoning emerges during training.

Token Assorted: Mixing Latent and Text Tokens for Improved Language Model Reasoning

Large Language Models (LLMs) excel at reasoning and planning when trained on chainof-thought (CoT) data, where the step-by-step thought process is explicitly outlined by text tokens. However, this results in lengthy inputs where many words support textual coherence rather than core reasoning information, and processing these inputs consumes substantial computation resources. In this work, we propose a hybrid representation of the reasoning process, where we partially abstract away the initial reasoning steps using latent discrete tokens generated by VQ-VAE, significantly reducing the length of reasoning traces. We explore the use of latent trace abstractions in two scenarios: 1) training the model from scratch for the Keys-Finding Maze problem, 2) fine-tuning LLMs on this hybrid data with an extended vocabulary including unseen latent tokens, for both logical and mathematical reasoning problems. To facilitate effective learning, we introduce a simple training procedure that randomly mixes latent and text tokens, which enables fast adaptation to new latent tokens. Our approach consistently outperforms the baselines methods in various benchmarks.

Avoiding Catastrophe in Continuous Spaces by Asking for Help

Most reinforcement learning algorithms with formal regret guarantees assume all mistakes are reversible and rely on essentially trying all possible options. This approach leads to poor outcomes when some mistakes are irreparable or even catastrophic. We propose a variant of the contextual bandit problem where the goal is to minimize the chance of catastrophe. Specifically, we assume that the payoff each round represents the chance of avoiding catastrophe that round, and try to maximize the product of payoffs (the overall chance of avoiding catastrophe). To give the agent some chance of success, we allow a limited number of queries to a mentor and assume a Lipschitz continuous payoff function. We present an algorithm whose regret and rate of querying the mentor both approach 0 as the time horizon grows, assuming a continuous 1D state space and a relatively "simple" payoff function. We also provide a matching lower bound: without the simplicity assumption: any algorithm either constantly asks for help or is nearly guaranteed to cause catastrophe. Finally, we identify the key obstacle to generalizing our algorithm to a multi-dimensional state space.

Efficient Prompt Caching via Embedding Similarity

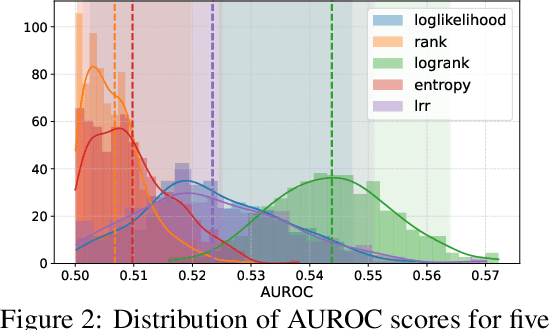
Large language models (LLMs) have achieved huge success in numerous natural language process (NLP) tasks. However, it faces the challenge of significant resource consumption during inference. In this paper, we aim to improve the inference efficiency of LLMs by prompt caching, i.e., if the current prompt can be answered by the same response of a previous prompt, one can directly utilize that previous response without calling the LLM. Specifically, we focus on the prediction accuracy of prompt caching for single-round question-answering tasks via embedding similarity. The existing embeddings of prompts mostly focus on whether two prompts are semantically similar, which is not necessarily equivalent to whether the same response can answer them. Therefore, we propose a distillation-based method to fine-tune the existing embeddings for better caching prediction. Theoretically, we provide finite-sample guarantees for the convergence of our method under different types of loss functions. Empirically, we carefully construct a hard dataset based on Kwiatkowski et al. (2019) where the existing embedding model (Wang et al., 2022) only achieves an AUC of 0.51. We then fine-tune the above embedding model, which significantly improves the AUC of caching prediction from 0.51 to 0.81. We also conduct simulations demonstrating that our trained models achieve better caching efficiency than the previous embedding model.

Towards Optimal Statistical Watermarking

We study statistical watermarking by formulating it as a hypothesis testing problem, a general framework which subsumes all previous statistical watermarking methods. Key to our formulation is a coupling of the output tokens and the rejection region, realized by pseudo-random generators in practice, that allows non-trivial trade-off between the Type I error and Type II error. We characterize the Uniformly Most Powerful (UMP) watermark in this context. In the most common scenario where the output is a sequence of $n$ tokens, we establish matching upper and lower bounds on the number of i.i.d. tokens required to guarantee small Type I and Type II errors. Our rate scales as $\Theta(h^{-1} \log (1/h))$ with respect to the average entropy per token $h$ and thus greatly improves the $O(h^{-2})$ rate in the previous works. For scenarios where the detector lacks knowledge of the model's distribution, we introduce the concept of model-agnostic watermarking and establish the minimax bounds for the resultant increase in Type II error. Moreover, we formulate the robust watermarking problem where user is allowed to perform a class of perturbation on the generated texts, and characterize the optimal type II error of robust UMP tests via a linear programming problem. To the best of our knowledge, this is the first systematic statistical treatment on the watermarking problem with near-optimal rates in the i.i.d. setting, and might be of interest for future works.

End-to-end Story Plot Generator

Story plots, while short, carry most of the essential information of a full story that may contain tens of thousands of words. We study the problem of automatic generation of story plots, which includes story premise, character descriptions, plot outlines, etc. To generate a single engaging plot, existing plot generators (e.g., DOC (Yang et al., 2022a)) require hundreds to thousands of calls to LLMs (e.g., OpenAI API) in the planning stage of the story plot, which is costly and takes at least several minutes. Moreover, the hard-wired nature of the method makes the pipeline non-differentiable, blocking fast specialization and personalization of the plot generator. In this paper, we propose three models, $\texttt{OpenPlot}$, $\texttt{E2EPlot}$ and $\texttt{RLPlot}$, to address these challenges. $\texttt{OpenPlot}$ replaces expensive OpenAI API calls with LLaMA2 (Touvron et al., 2023) calls via careful prompt designs, which leads to inexpensive generation of high-quality training datasets of story plots. We then train an end-to-end story plot generator, $\texttt{E2EPlot}$, by supervised fine-tuning (SFT) using approximately 13000 story plots generated by $\texttt{OpenPlot}$. $\texttt{E2EPlot}$ generates story plots of comparable quality to $\texttt{OpenPlot}$, and is > 10$\times$ faster (1k tokens in only 30 seconds on average). Finally, we obtain $\texttt{RLPlot}$ that is further fine-tuned with RLHF on several different reward models for different aspects of story quality, which yields 60.0$\%$ winning rate against $\texttt{E2EPlot}$ along the aspect of suspense and surprise.

Learning Personalized Story Evaluation

While large language models (LLMs) have shown impressive results for more objective tasks such as QA and retrieval, it remains nontrivial to evaluate their performance on open-ended text generation for reasons including (1) data contamination; (2) multi-dimensional evaluation criteria; and (3) subjectiveness stemming from reviewers' personal preferences. To address such issues, we propose to model personalization in an uncontaminated open-ended generation assessment. We create two new datasets Per-MPST and Per-DOC for personalized story evaluation, by re-purposing existing datasets with proper anonymization and new personalized labels. We further develop a personalized story evaluation model PERSE to infer reviewer preferences and provide a personalized evaluation. Specifically, given a few exemplary reviews from a particular reviewer, PERSE predicts either a detailed review or fine-grained comparison in several aspects (such as interestingness and surprise) for that reviewer on a new text input. Experimental results show that PERSE outperforms GPT-4 by 15.8% on Kendall correlation of story ratings, and by 13.7% on pairwise preference prediction accuracy. Both datasets and code will be released.

On Representation Complexity of Model-based and Model-free Reinforcement Learning

We study the representation complexity of model-based and model-free reinforcement learning (RL) in the context of circuit complexity. We prove theoretically that there exists a broad class of MDPs such that their underlying transition and reward functions can be represented by constant depth circuits with polynomial size, while the optimal $Q$-function suffers an exponential circuit complexity in constant-depth circuits. By drawing attention to the approximation errors and building connections to complexity theory, our theory provides unique insights into why model-based algorithms usually enjoy better sample complexity than model-free algorithms from a novel representation complexity perspective: in some cases, the ground-truth rule (model) of the environment is simple to represent, while other quantities, such as $Q$-function, appear complex. We empirically corroborate our theory by comparing the approximation error of the transition kernel, reward function, and optimal $Q$-function in various Mujoco environments, which demonstrates that the approximation errors of the transition kernel and reward function are consistently lower than those of the optimal $Q$-function. To the best of our knowledge, this work is the first to study the circuit complexity of RL, which also provides a rigorous framework for future research.