Stable Marriage Problems with Ties and Incomplete Preferences: An Empirical Comparison of ASP, SAT, ILP, CP, and Local Search Methods

We study a variation of the Stable Marriage problem, where every man and every woman express their preferences as preference lists which may be incomplete and contain ties. This problem is called the Stable Marriage problem with Ties and Incomplete preferences (SMTI). We consider three optimization variants of SMTI, Max Cardinality, Sex-Equal and Egalitarian, and empirically compare the following methods to solve them: Answer Set Programming, Constraint Programming, Integer Linear Programming. For Max Cardinality, we compare these methods with Local Search methods as well. We also empirically compare Answer Set Programming with Propositional Satisfiability, for SMTI instances. This paper is under consideration for acceptance in Theory and Practice of Logic Programming (TPLP).

Knowledge-Based Stable Roommates Problem: A Real-World Application

The Stable Roommates problem with Ties and Incomplete lists (SRTI) is a matching problem characterized by the preferences of agents over other agents as roommates, where the preferences may have ties or be incomplete. SRTI asks for a matching that is stable and, sometimes, optimizes a domain-independent fairness criterion (e.g., Egalitarian). However, in real-world applications (e.g., assigning students as roommates at a dormitory), we usually consider a variety of domain-specific criteria depending on preferences over the habits and desires of the agents. With this motivation, we introduce a knowledge-based method to SRTI considering domain-specific knowledge, and investigate its real-world application for assigning students as roommates at a university dormitory. This paper is under consideration for acceptance in Theory and Practice of Logic Programming (TPLP).

A General Framework for Stable Roommates Problems using Answer Set Programming

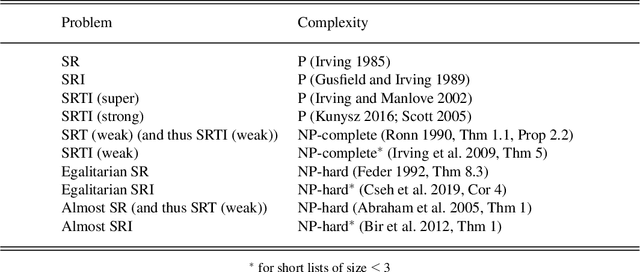
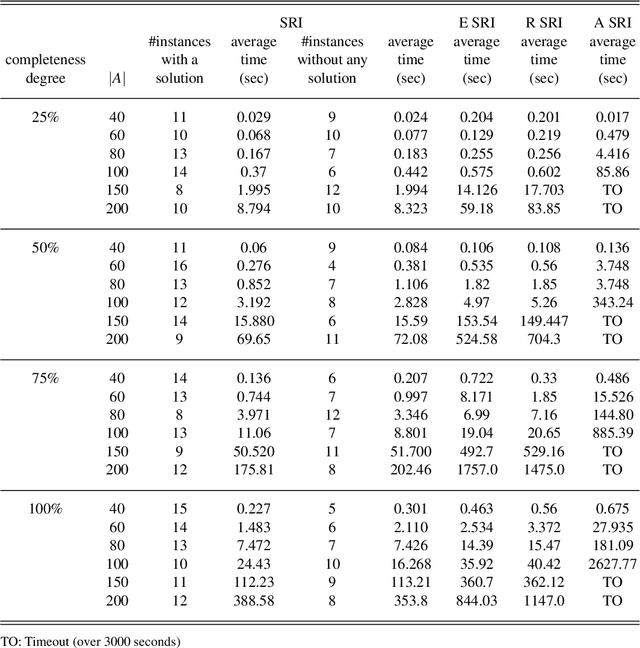
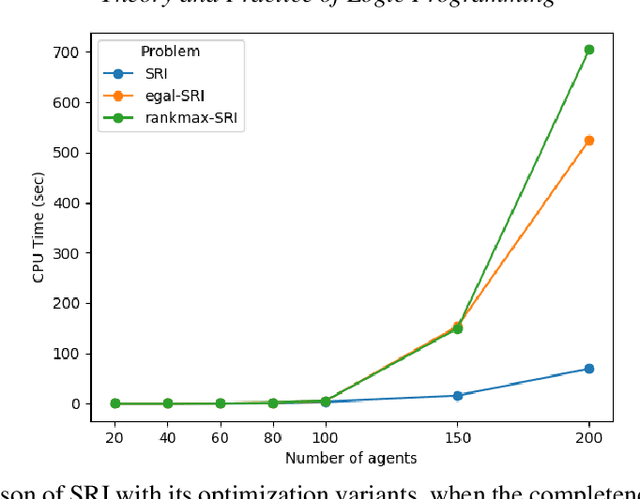
The Stable Roommates problem (SR) is characterized by the preferences of agents over other agents as roommates: each agent ranks all others in strict order of preference. A solution to SR is then a partition of the agents into pairs so that each pair shares a room, and there is no pair of agents that would block this matching (i.e., who prefers the other to their roommate in the matching). There are interesting variations of SR that are motivated by applications (e.g., the preference lists may be incomplete (SRI) and involve ties (SRTI)), and that try to find a more fair solution (e.g., Egalitarian SR). Unlike the Stable Marriage problem, every SR instance is not guaranteed to have a solution. For that reason, there are also variations of SR that try to find a good-enough solution (e.g., Almost SR). Most of these variations are NP-hard. We introduce a formal framework, called SRTI-ASP, utilizing the logic programming paradigm Answer Set Programming, that is provable and general enough to solve many of such variations of SR. Our empirical analysis shows that SRTI-ASP is also promising for applications. This paper is under consideration for acceptance in TPLP.