Preference Elicitation for Step-Wise Explanations in Logic Puzzles

Step-wise explanations can explain logic puzzles and other satisfaction problems by showing how to derive decisions step by step. Each step consists of a set of constraints that derive an assignment to one or more decision variables. However, many candidate explanation steps exist, with different sets of constraints and different decisions they derive. To identify the most comprehensible one, a user-defined objective function is required to quantify the quality of each step. However, defining a good objective function is challenging. Here, interactive preference elicitation methods from the wider machine learning community can offer a way to learn user preferences from pairwise comparisons. We investigate the feasibility of this approach for step-wise explanations and address several limitations that distinguish it from elicitation for standard combinatorial problems. First, because the explanation quality is measured using multiple sub-objectives that can vary a lot in scale, we propose two dynamic normalization techniques to rescale these features and stabilize the learning process. We also observed that many generated comparisons involve similar explanations. For this reason, we introduce MACHOP (Multi-Armed CHOice Perceptron), a novel query generation strategy that integrates non-domination constraints with upper confidence bound-based diversification. We evaluate the elicitation techniques on Sudokus and Logic-Grid puzzles using artificial users, and validate them with a real-user evaluation. In both settings, MACHOP consistently produces higher-quality explanations than the standard approach.

Using Certifying Constraint Solvers for Generating Step-wise Explanations

In the field of Explainable Constraint Solving, it is common to explain to a user why a problem is unsatisfiable. A recently proposed method for this is to compute a sequence of explanation steps. Such a step-wise explanation shows individual reasoning steps involving constraints from the original specification, that in the end explain a conflict. However, computing a step-wise explanation is computationally expensive, limiting the scope of problems for which it can be used. We investigate how we can use proofs generated by a constraint solver as a starting point for computing step-wise explanations, instead of computing them step-by-step. More specifically, we define a framework of abstract proofs, in which both proofs and step-wise explanations can be represented. We then propose several methods for converting a proof to a step-wise explanation sequence, with special attention to trimming and simplification techniques to keep the sequence and its individual steps small. Our results show our method significantly speeds up the generation of step-wise explanation sequences, while the resulting step-wise explanation has a quality similar to the current state-of-the-art.

Efficient and Reliable Hitting-Set Computations for the Implicit Hitting Set Approach

The implicit hitting set (IHS) approach offers a general framework for solving computationally hard combinatorial optimization problems declaratively. IHS iterates between a decision oracle used for extracting sources of inconsistency and an optimizer for computing so-called hitting sets (HSs) over the accumulated sources of inconsistency. While the decision oracle is language-specific, the optimizers is usually instantiated through integer programming. We explore alternative algorithmic techniques for hitting set optimization based on different ways of employing pseudo-Boolean (PB) reasoning as well as stochastic local search. We extensively evaluate the practical feasibility of the alternatives in particular in the context of pseudo-Boolean (0-1 IP) optimization as one of the most recent instantiations of IHS. Highlighting a trade-off between efficiency and reliability, while a commercial IP solver turns out to remain the most effective way to instantiate HS computations, it can cause correctness issues due to numerical instability; in fact, we show that exact HS computations instantiated via PB reasoning can be made competitive with a numerically exact IP solver. Furthermore, the use of PB reasoning as a basis for HS computations allows for obtaining certificates for the correctness of IHS computations, generally applicable to any IHS instantiation in which reasoning in the declarative language at hand can be captured in the PB-based proof format we employ.

Certifying Pareto-Optimality in Multi-Objective Maximum Satisfiability

Due to the wide employment of automated reasoning in the analysis and construction of correct systems, the results reported by automated reasoning engines must be trustworthy. For Boolean satisfiability (SAT) solvers - and more recently SAT-based maximum satisfiability (MaxSAT) solvers - trustworthiness is obtained by integrating proof logging into solvers, making solvers capable of emitting machine-verifiable proofs to certify correctness of the reasoning steps performed. In this work, we enable for the first time proof logging based on the VeriPB proof format for multi-objective MaxSAT (MO-MaxSAT) optimization techniques. Although VeriPB does not offer direct support for multi-objective problems, we detail how preorders in VeriPB can be used to provide certificates for MO-MaxSAT algorithms computing a representative solution for each element in the non-dominated set of the search space under Pareto-optimality, without extending the VeriPB format or the proof checker. By implementing VeriPB proof logging into a state-of-the-art multi-objective MaxSAT solver, we show empirically that proof logging can be made scalable for MO-MaxSAT with reasonable overhead.

Exploiting Symmetries in MUS Computation (Extended version)

In eXplainable Constraint Solving (XCS), it is common to extract a Minimal Unsatisfiable Subset (MUS) from a set of unsatisfiable constraints. This helps explain to a user why a constraint specification does not admit a solution. Finding MUSes can be computationally expensive for highly symmetric problems, as many combinations of constraints need to be considered. In the traditional context of solving satisfaction problems, symmetry has been well studied, and effective ways to detect and exploit symmetries during the search exist. However, in the setting of finding MUSes of unsatisfiable constraint programs, symmetries are understudied. In this paper, we take inspiration from existing symmetry-handling techniques and adapt well-known MUS-computation methods to exploit symmetries in the specification, speeding-up overall computation time. Our results display a significant reduction of runtime for our adapted algorithms compared to the baseline on symmetric problems.

The Stable Model Semantics for Higher-Order Logic Programming

We propose a stable model semantics for higher-order logic programs. Our semantics is developed using Approximation Fixpoint Theory (AFT), a powerful formalism that has successfully been used to give meaning to diverse non-monotonic formalisms. The proposed semantics generalizes the classical two-valued stable model semantics of (Gelfond and Lifschitz 1988) as-well-as the three-valued one of (Przymusinski 1990), retaining their desirable properties. Due to the use of AFT, we also get for free alternative semantics for higher-order logic programs, namely supported model, Kripke-Kleene, and well-founded. Additionally, we define a broad class of stratified higher-order logic programs and demonstrate that they have a unique two-valued higher-order stable model which coincides with the well-founded semantics of such programs. We provide a number of examples in different application domains, which demonstrate that higher-order logic programming under the stable model semantics is a powerful and versatile formalism, which can potentially form the basis of novel ASP systems.

Using Symmetries to Lift Satisfiability Checking

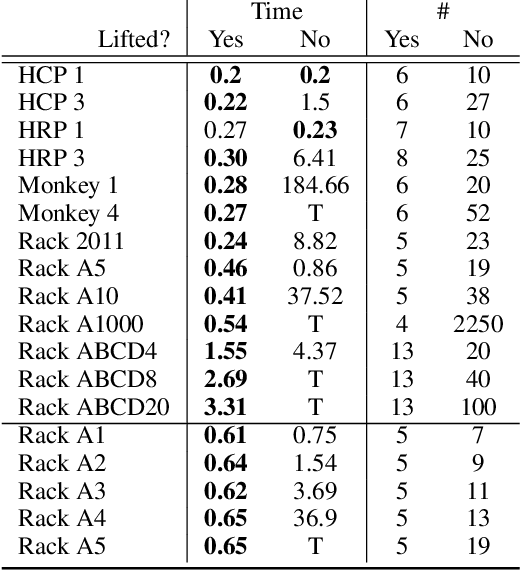
We analyze how symmetries can be used to compress structures (also known as interpretations) onto a smaller domain without loss of information. This analysis suggests the possibility to solve satisfiability problems in the compressed domain for better performance. Thus, we propose a 2-step novel method: (i) the sentence to be satisfied is automatically translated into an equisatisfiable sentence over a ``lifted'' vocabulary that allows domain compression; (ii) satisfiability of the lifted sentence is checked by growing the (initially unknown) compressed domain until a satisfying structure is found. The key issue is to ensure that this satisfying structure can always be expanded into an uncompressed structure that satisfies the original sentence to be satisfied. We present an adequate translation for sentences in typed first-order logic extended with aggregates. Our experimental evaluation shows large speedups for generative configuration problems. The method also has applications in the verification of software operating on complex data structures. Further refinements of the translation are left for future work.

Non-deterministic approximation operators: ultimate operators, semi-equilibrium semantics and aggregates (full version)

Approximation fixpoint theory (AFT) is an abstract and general algebraic framework for studying the semantics of non-monotonic logics. In recent work, AFT was generalized to non-deterministic operators, i.e.\ operators whose range are sets of elements rather than single elements. In this paper, we make three further contributions to non-deterministic AFT: (1) we define and study ultimate approximations of non-deterministic operators, (2) we give an algebraic formulation of the semi-equilibrium semantics by Amendola, et al., and (3) we generalize the characterisations of disjunctive logic programs to disjunctive logic programs with aggregates.

Efficiently Explaining CSPs with Unsatisfiable Subset Optimization (extended algorithms and examples)

We build on a recently proposed method for stepwise explaining solutions of Constraint Satisfaction Problems (CSP) in a human-understandable way. An explanation here is a sequence of simple inference steps where simplicity is quantified using a cost function. The algorithms for explanation generation rely on extracting Minimal Unsatisfiable Subsets (MUS) of a derived unsatisfiable formula, exploiting a one-to-one correspondence between so-called non-redundant explanations and MUSs. However, MUS extraction algorithms do not provide any guarantee of subset minimality or optimality with respect to a given cost function. Therefore, we build on these formal foundations and tackle the main points of improvement, namely how to generate explanations efficiently that are provably optimal (with respect to the given cost metric). For that, we developed (1) a hitting set-based algorithm for finding the optimal constrained unsatisfiable subsets; (2) a method for re-using relevant information over multiple algorithm calls; and (3) methods exploiting domain-specific information to speed up the explanation sequence generation. We experimentally validated our algorithms on a large number of CSP problems. We found that our algorithms outperform the MUS approach in terms of explanation quality and computational time (on average up to 56 % faster than a standard MUS approach).

Distributed Subweb Specifications for Traversing the Web

Link Traversal-based Query Processing (ltqp), in which a sparql query is evaluated over a web of documents rather than a single dataset, is often seen as a theoretically interesting yet impractical technique. However, in a time where the hypercentralization of data has increasingly come under scrutiny, a decentralized Web of Data with a simple document-based interface is appealing, as it enables data publishers to control their data and access rights. While ltqp allows evaluating complex queries over such webs, it suffers from performance issues (due to the high number of documents containing data) as well as information quality concerns (due to the many sources providing such documents). In existing ltqp approaches, the burden of finding sources to query is entirely in the hands of the data consumer. In this paper, we argue that to solve these issues, data publishers should also be able to suggest sources of interest and guide the data consumer towards relevant and trustworthy data. We introduce a theoretical framework that enables such guided link traversal and study its properties. We illustrate with a theoretic example that this can improve query results and reduce the number of network requests. We evaluate our proposal experimentally on a virtual linked web with specifications and indeed observe that not just the data quality but also the efficiency of querying improves. Under consideration in Theory and Practice of Logic Programming (TPLP).