Using Symmetries to Lift Satisfiability Checking

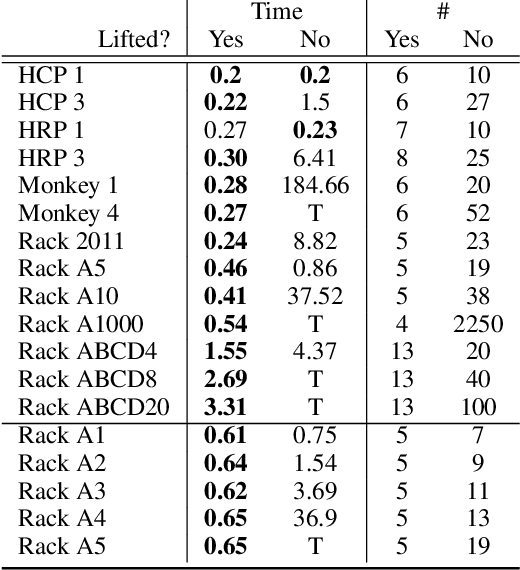
We analyze how symmetries can be used to compress structures (also known as interpretations) onto a smaller domain without loss of information. This analysis suggests the possibility to solve satisfiability problems in the compressed domain for better performance. Thus, we propose a 2-step novel method: (i) the sentence to be satisfied is automatically translated into an equisatisfiable sentence over a ``lifted'' vocabulary that allows domain compression; (ii) satisfiability of the lifted sentence is checked by growing the (initially unknown) compressed domain until a satisfying structure is found. The key issue is to ensure that this satisfying structure can always be expanded into an uncompressed structure that satisfies the original sentence to be satisfied. We present an adequate translation for sentences in typed first-order logic extended with aggregates. Our experimental evaluation shows large speedups for generative configuration problems. The method also has applications in the verification of software operating on complex data structures. Further refinements of the translation are left for future work.

Analyzing Semantics of Aggregate Answer Set Programming Using Approximation Fixpoint Theory

Aggregates provide a concise way to express complex knowledge. While they are easily understood by humans, formalizing aggregates for answer set programming (ASP) has proven to be challenging . The literature offers many approaches that are not always compatible. One of these approaches, based on Approximation Fixpoint Theory (AFT), has been developed in a logic programming context and has not found much resonance in the ASP-community. In this paper we revisit this work. We introduce the abstract notion of a ternary satisfaction relation and define stable semantics in terms of it. We show that ternary satisfaction relations bridge the gap between the standard Gelfond-Lifschitz reduct, and stable semantics as defined in the framework of AFT. We analyse the properties of ternary satisfaction relations for handling aggregates in ASP programs. Finally, we show how different methods for handling aggregates taken from the literature can be described in the framework and we study the corresponding ternary satisfaction relations.

A MIP Backend for the IDP System

The IDP knowledge base system currently uses MiniSAT(ID) as its backend Constraint Programming (CP) solver. A few similar systems have used a Mixed Integer Programming (MIP) solver as backend. However, so far little is known about when the MIP solver is preferable. This paper explores this question. It describes the use of CPLEX as a backend for IDP and reports on experiments comparing both backends.

Predicate Logic as a Modeling Language: Modeling and Solving some Machine Learning and Data Mining Problems with IDP3

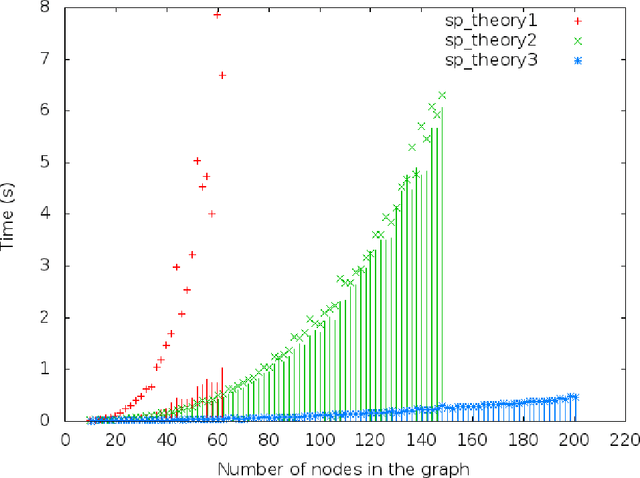
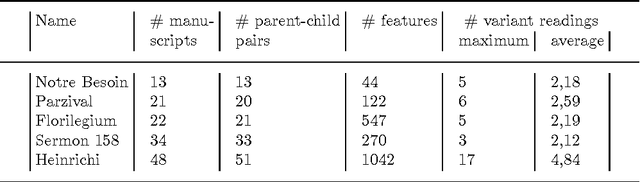
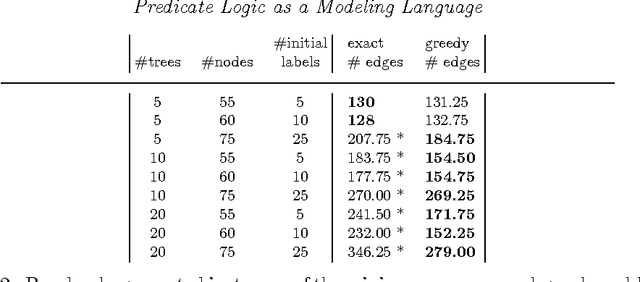
This paper provides a gentle introduction to problem solving with the IDP3 system. The core of IDP3 is a finite model generator that supports first order logic enriched with types, inductive definitions, aggregates and partial functions. It offers its users a modeling language that is a slight extension of predicate logic and allows them to solve a wide range of search problems. Apart from a small introductory example, applications are selected from problems that arose within machine learning and data mining research. These research areas have recently shown a strong interest in declarative modeling and constraint solving as opposed to algorithmic approaches. The paper illustrates that the IDP3 system can be a valuable tool for researchers with such an interest. The first problem is in the domain of stemmatology, a domain of philology concerned with the relationship between surviving variant versions of text. The second problem is about a somewhat related problem within biology where phylogenetic trees are used to represent the evolution of species. The third and final problem concerns the classical problem of learning a minimal automaton consistent with a given set of strings. For this last problem, we show that the performance of our solution comes very close to that of a state-of-the art solution. For each of these applications, we analyze the problem, illustrate the development of a logic-based model and explore how alternatives can affect the performance.

Constraint Propagation for First-Order Logic and Inductive Definitions

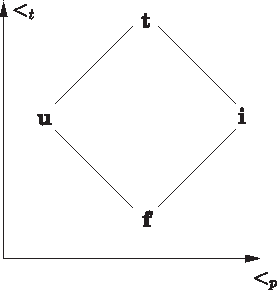
Constraint propagation is one of the basic forms of inference in many logic-based reasoning systems. In this paper, we investigate constraint propagation for first-order logic (FO), a suitable language to express a wide variety of constraints. We present an algorithm with polynomial-time data complexity for constraint propagation in the context of an FO theory and a finite structure. We show that constraint propagation in this manner can be represented by a datalog program and that the algorithm can be executed symbolically, i.e., independently of a structure. Next, we extend the algorithm to FO(ID), the extension of FO with inductive definitions. Finally, we discuss several applications.

CP-logic: A Language of Causal Probabilistic Events and Its Relation to Logic Programming

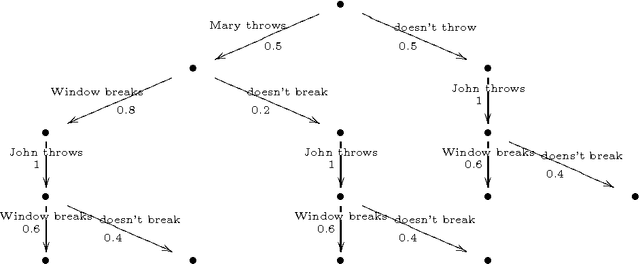
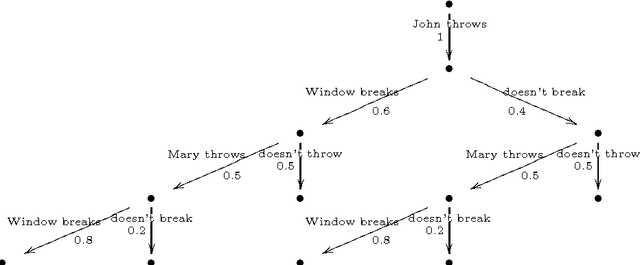
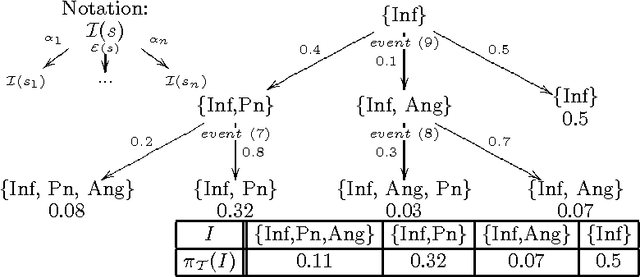
This papers develops a logical language for representing probabilistic causal laws. Our interest in such a language is twofold. First, it can be motivated as a fundamental study of the representation of causal knowledge. Causality has an inherent dynamic aspect, which has been studied at the semantical level by Shafer in his framework of probability trees. In such a dynamic context, where the evolution of a domain over time is considered, the idea of a causal law as something which guides this evolution is quite natural. In our formalization, a set of probabilistic causal laws can be used to represent a class of probability trees in a concise, flexible and modular way. In this way, our work extends Shafer's by offering a convenient logical representation for his semantical objects. Second, this language also has relevance for the area of probabilistic logic programming. In particular, we prove that the formal semantics of a theory in our language can be equivalently defined as a probability distribution over the well-founded models of certain logic programs, rendering it formally quite similar to existing languages such as ICL or PRISM. Because we can motivate and explain our language in a completely self-contained way as a representation of probabilistic causal laws, this provides a new way of explaining the intuitions behind such probabilistic logic programs: we can say precisely which knowledge such a program expresses, in terms that are equally understandable by a non-logician. Moreover, we also obtain an additional piece of knowledge representation methodology for probabilistic logic programs, by showing how they can express probabilistic causal laws.

Enhancing a Search Algorithm to Perform Intelligent Backtracking

This paper illustrates how a Prolog program, using chronological backtracking to find a solution in some search space, can be enhanced to perform intelligent backtracking. The enhancement crucially relies on the impurity of Prolog that allows a program to store information when a dead end is reached. To illustrate the technique, a simple search program is enhanced. To appear in Theory and Practice of Logic Programming. Keywords: intelligent backtracking, dependency-directed backtracking, backjumping, conflict-directed backjumping, nogood sets, look-back.

Offline Specialisation in Prolog Using a Hand-Written Compiler Generator

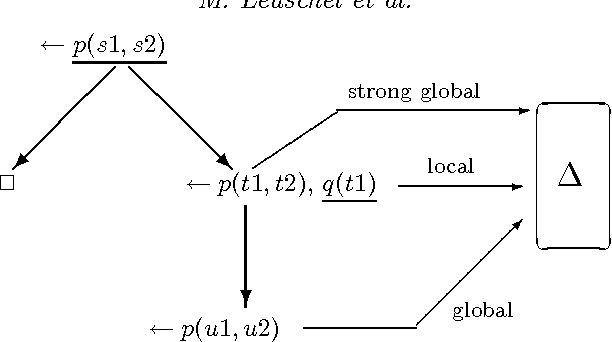
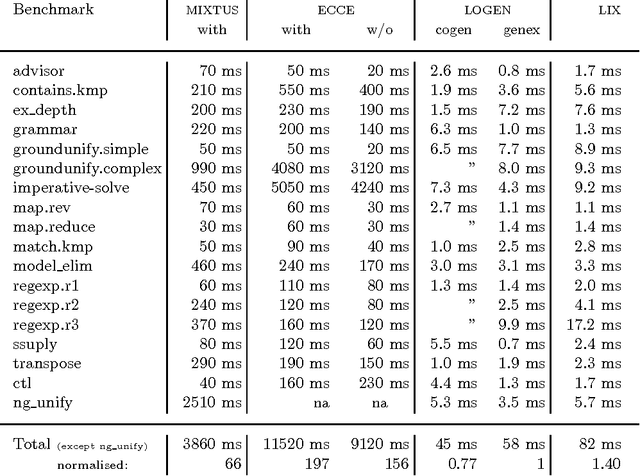
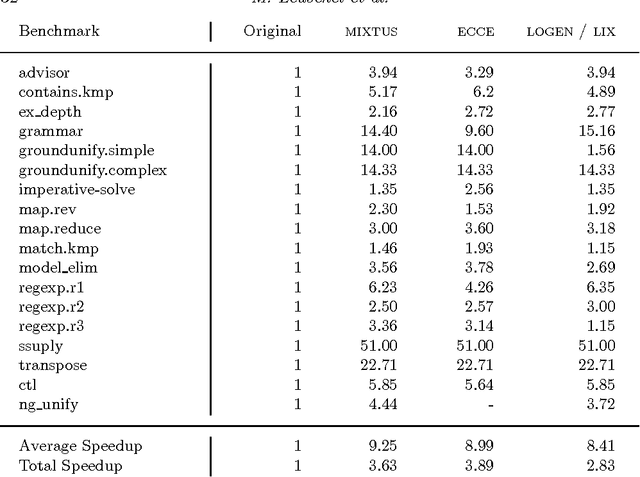
The so called ``cogen approach'' to program specialisation, writing a compiler generator instead of a specialiser, has been used with considerable success in partial evaluation of both functional and imperative languages. This paper demonstrates that the cogen approach is also applicable to the specialisation of logic programs (also called partial deduction) and leads to effective specialisers. Moreover, using good binding-time annotations, the speed-ups of the specialised programs are comparable to the speed-ups obtained with online specialisers. The paper first develops a generic approach to offline partial deduction and then a specific offline partial deduction method, leading to the offline system LIX for pure logic programs. While this is a usable specialiser by itself, it is used to develop the cogen system LOGEN. Given a program, a specification of what inputs will be static, and an annotation specifying which calls should be unfolded, LOGEN generates a specialised specialiser for the program at hand. Running this specialiser with particular values for the static inputs results in the specialised program. While this requires two steps instead of one, the efficiency of the specialisation process is improved in situations where the same program is specialised multiple times. The paper also presents and evaluates an automatic binding-time analysis that is able to derive the annotations. While the derived annotations are still suboptimal compared to hand-crafted ones, they enable non-expert users to use the LOGEN system in a fully automated way. Finally, LOGEN is extended so as to directly support a large part of Prolog's declarative and non-declarative features and so as to be able to perform so called mixline specialisations.

Logic program specialisation through partial deduction: Control issues

Program specialisation aims at improving the overall performance of programs by performing source to source transformations. A common approach within functional and logic programming, known respectively as partial evaluation and partial deduction, is to exploit partial knowledge about the input. It is achieved through a well-automated application of parts of the Burstall-Darlington unfold/fold transformation framework. The main challenge in developing systems is to design automatic control that ensures correctness, efficiency, and termination. This survey and tutorial presents the main developments in controlling partial deduction over the past 10 years and analyses their respective merits and shortcomings. It ends with an assessment of current achievements and sketches some remaining research challenges.

Detecting Unsolvable Queries for Definite Logic Programs

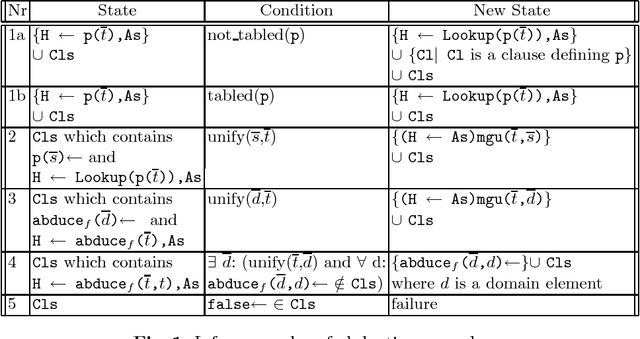
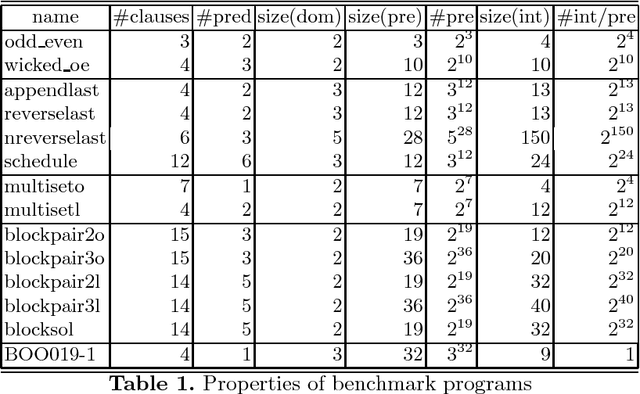
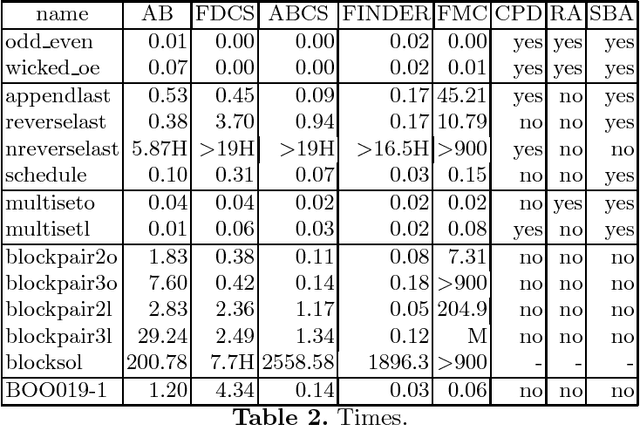
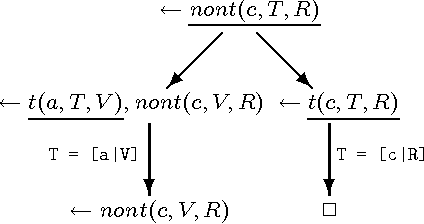
In solving a query, the SLD proof procedure for definite programs sometimes searches an infinite space for a non existing solution. For example, querying a planner for an unreachable goal state. Such programs motivate the development of methods to prove the absence of a solution. Considering the definite program and the query ``<- Q'' as clauses of a first order theory, one can apply model generators which search for a finite interpretation in which the program clauses as well as the clause ``false <- Q'' are true. This paper develops a new approach which exploits the fact that all clauses are definite. It is based on a goal directed abductive search in the space of finite pre-interpretations for a pre-interpretation such that ``Q'' is false in the least model of the program based on it. Several methods for efficiently searching the space of pre-interpretations are presented. Experimental results confirm that our approach find solutions with less search than with the use of a first order model generator.