Patrick De Causmaecker
Features for the 0-1 knapsack problem based on inclusionwise maximal solutions
Nov 16, 2022Abstract:Decades of research on the 0-1 knapsack problem led to very efficient algorithms that are able to quickly solve large problem instances to optimality. This prompted researchers to also investigate whether relatively small problem instances exist that are hard for existing solvers and investigate which features characterize their hardness. Previously the authors proposed a new class of hard 0-1 knapsack problem instances and demonstrated that the properties of so-called inclusionwise maximal solutions (IMSs) can be important hardness indicators for this class. In the current paper, we formulate several new computationally challenging problems related to the IMSs of arbitrary 0-1 knapsack problem instances. Based on generalizations of previous work and new structural results about IMSs, we formulate polynomial and pseudopolynomial time algorithms for solving these problems. From this we derive a set of 14 computationally expensive features, which we calculate for two large datasets on a supercomputer in approximately 540 CPU-hours. We show that the proposed features contain important information related to the empirical hardness of a problem instance that was missing in earlier features from the literature by training machine learning models that can accurately predict the empirical hardness of a wide variety of 0-1 knapsack problem instances. Using the instance space analysis methodology, we also show that hard 0-1 knapsack problem instances are clustered together around a relatively dense region of the instance space and several features behave differently in the easy and hard parts of the instance space.
A prediction-based approach for online dynamic radiotherapy scheduling
Dec 16, 2021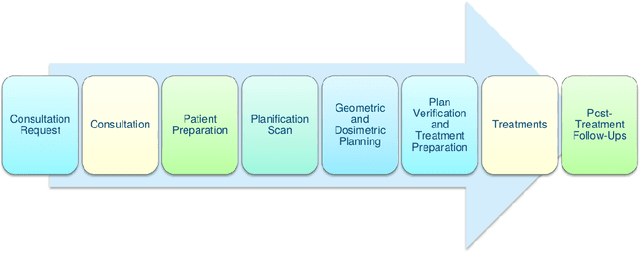
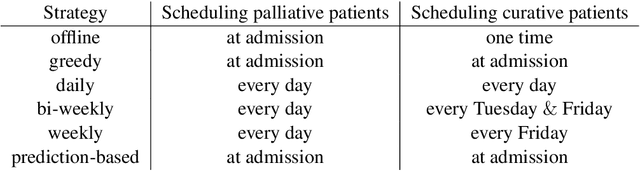
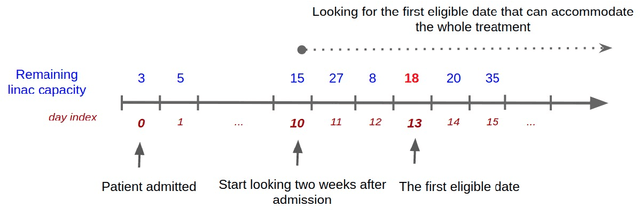
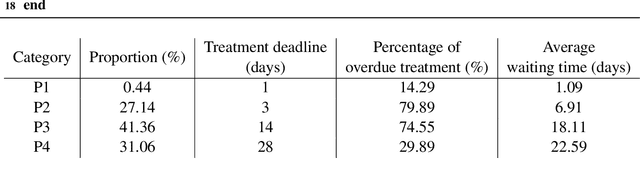
Abstract:Patient scheduling is a difficult task as it involves dealing with stochastic factors such as an unknown arrival flow of patients. Scheduling radiotherapy treatments for cancer patients faces a similar problem. Curative patients need to start their treatment within the recommended deadlines, i.e., 14 or 28 days after their admission while reserving treatment capacity for palliative patients who require urgent treatments within 1 to 3 days after their admission. Most cancer centers solve the problem by reserving a fixed number of treatment slots for emergency patients. However, this flat-reservation approach is not ideal and can cause overdue treatments for emergency patients on some days while not fully exploiting treatment capacity on some other days, which also leads to delaying treatment for curative patients. This problem is especially severe in large and crowded hospitals. In this paper, we propose a prediction-based approach for online dynamic radiotherapy scheduling. An offline problem where all future patient arrivals are known in advance is solved to optimality using Integer Programming. A regression model is then trained to recognize the links between patients' arrival patterns and their ideal waiting time. The trained regression model is then embedded in a prediction-based approach that schedules a patient based on their characteristics and the present state of the calendar. The numerical results show that our prediction-based approach efficiently prevents overdue treatments for emergency patients while maintaining a good waiting time compared to other scheduling approaches based on a flat-reservation policy.
Neural Networked Assisted Tree Search for the Personnel Rostering Problem
Oct 24, 2020
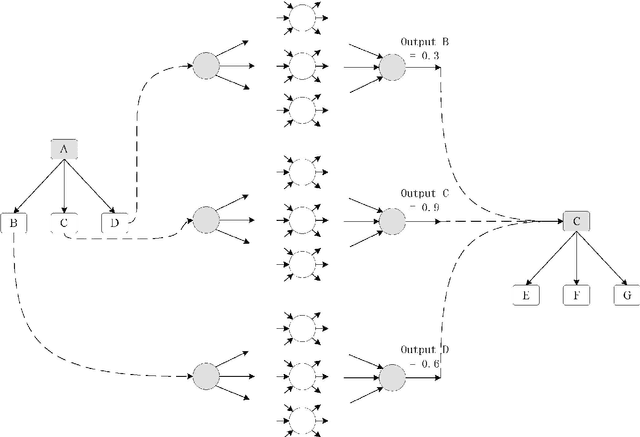

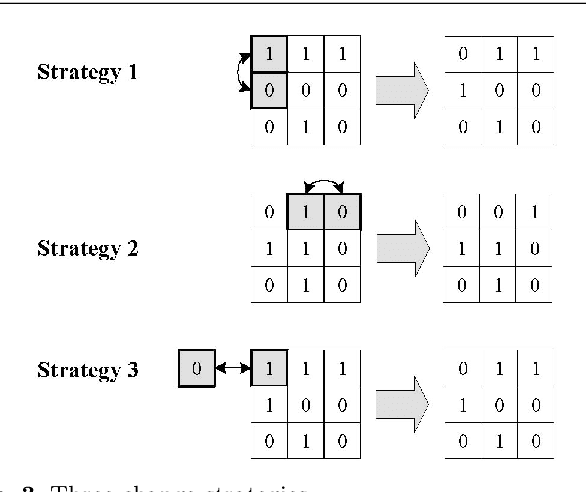
Abstract:The personnel rostering problem is the problem of finding an optimal way to assign employees to shifts, subject to a set of hard constraints which all valid solutions must follow, and a set of soft constraints which define the relative quality of valid solutions. The problem has received significant attention in the literature and is addressed by a large number of exact and metaheuristic methods. In order to make the complex and costly design of heuristics for the personnel rostering problem automatic, we propose a new method combined Deep Neural Network and Tree Search. By treating schedules as matrices, the neural network can predict the distance between the current solution and the optimal solution. It can select solution strategies by analyzing existing (near-)optimal solutions to personnel rostering problem instances. Combined with branch and bound, the network can give every node a probability which indicates the distance between it and the optimal one, so that a well-informed choice can be made on which branch to choose next and to prune the search tree.
Exploring search space trees using an adapted version of Monte Carlo tree search for a combinatorial optimization problem
Oct 22, 2020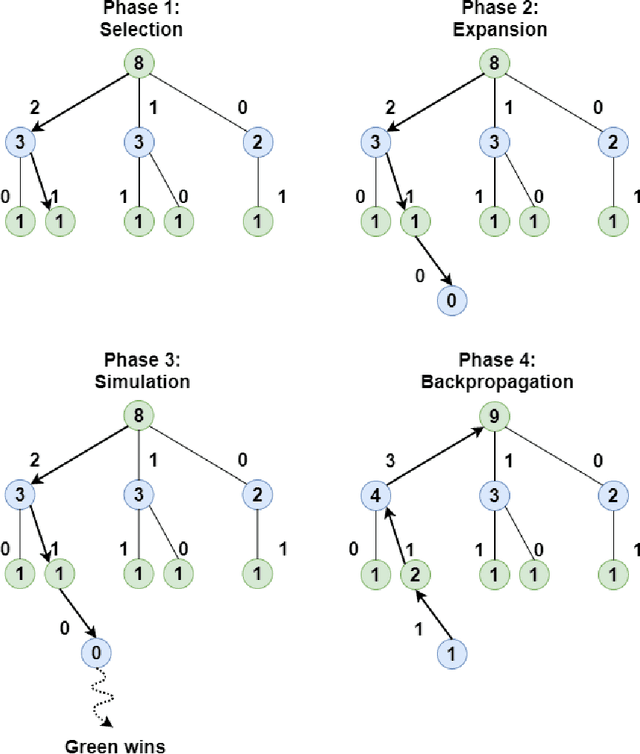

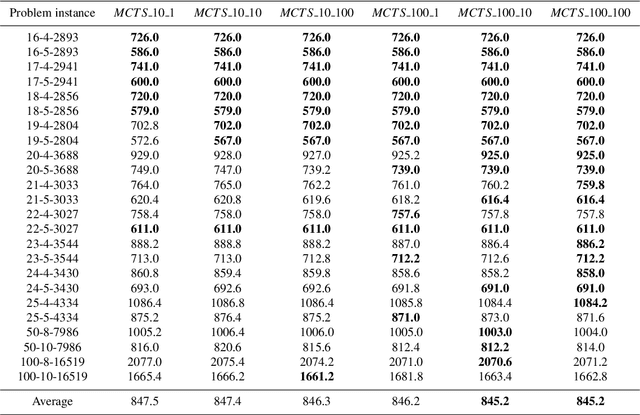
Abstract:In this article, a novel approach to solve combinatorial optimization problems is proposed. This approach makes use of a heuristic algorithm to explore the search space tree of a problem instance. The algorithm is based on Monte Carlo tree search, a popular algorithm in game playing that is used to explore game trees. By leveraging the combinatorial structure of a problem, several enhancements to the algorithm are proposed. These enhancements aim to efficiently explore the search space tree by pruning subtrees, using a heuristic simulation policy, reducing the domain of variables by eliminating dominated solutions and using a beam width. They are demonstrated for a specific combinatorial optimization problem: the quay crane scheduling problem with non-crossing constraints. Computational results show that the proposed algorithm is competitive with the state-of-the-art for this problem and eight new best solutions for a benchmark set of instances are found. Apart from this, the results also show evidence that the algorithm is able to learn to correct the incorrect choices of a standard heuristic, yielding an average improvement of 10.0 % with respect to the objective function value of the solution.
Solving the Steiner Tree Problem in graphs with Variable Neighborhood Descent
Jun 13, 2018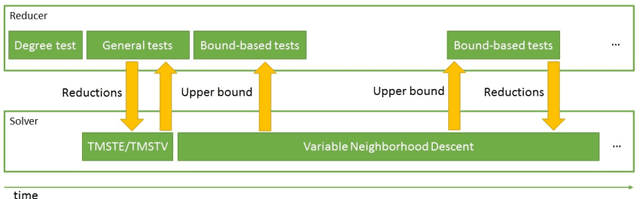
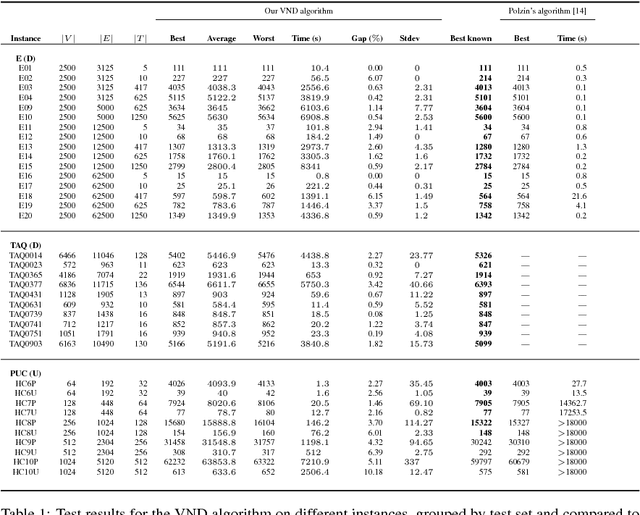
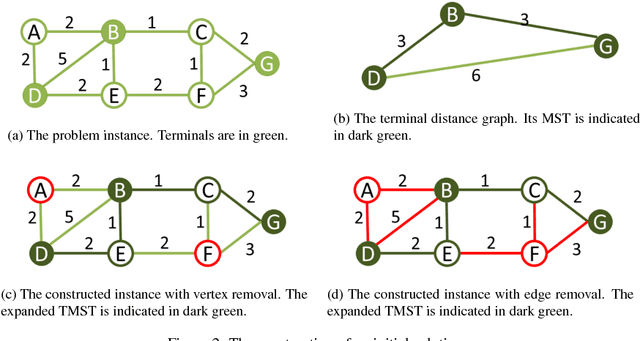
Abstract:The Steiner Tree Problem (STP) in graphs is an important problem with various applications in many areas such as design of integrated circuits, evolution theory, networking, etc. In this paper, we propose an algorithm to solve the STP. The algorithm includes a reducer and a solver using Variable Neighborhood Descent (VND), interacting with each other during the search. New constructive heuristics and a vertex score system for intensification purpose are proposed. The algorithm is tested on a set of benchmarks which shows encouraging results.
A MIP Backend for the IDP System
Sep 02, 2016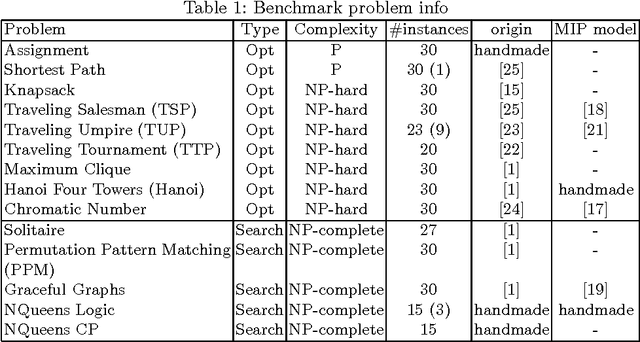


Abstract:The IDP knowledge base system currently uses MiniSAT(ID) as its backend Constraint Programming (CP) solver. A few similar systems have used a Mixed Integer Programming (MIP) solver as backend. However, so far little is known about when the MIP solver is preferable. This paper explores this question. It describes the use of CPLEX as a backend for IDP and reports on experiments comparing both backends.
Characterization of neighborhood behaviours in a multi-neighborhood local search algorithm
Mar 12, 2016



Abstract:We consider a multi-neighborhood local search algorithm with a large number of possible neighborhoods. Each neighborhood is accompanied by a weight value which represents the probability of being chosen at each iteration. These weights are fixed before the algorithm runs, and are considered as parameters of the algorithm. Given a set of instances, off-line tuning of the algorithm's parameters can be done by automated algorithm configuration tools (e.g., SMAC). However, the large number of neighborhoods can make the tuning expensive and difficult even when the number of parameters has been reduced by some intuition. In this work, we propose a systematic method to characterize each neighborhood's behaviours, representing them as a feature vector, and using cluster analysis to form similar groups of neighborhoods. The novelty of our characterization method is the ability of reflecting changes of behaviours according to hardness of different solution quality regions. We show that using neighborhood clusters instead of individual neighborhoods helps to reduce the parameter configuration space without misleading the search of the tuning procedure. Moreover, this method is problem-independent and potentially can be applied in similar contexts.
Second International Nurse Rostering Competition (INRC-II) --- Problem Description and Rules ---
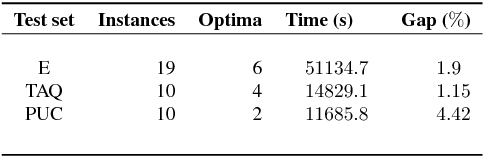
Jan 17, 2015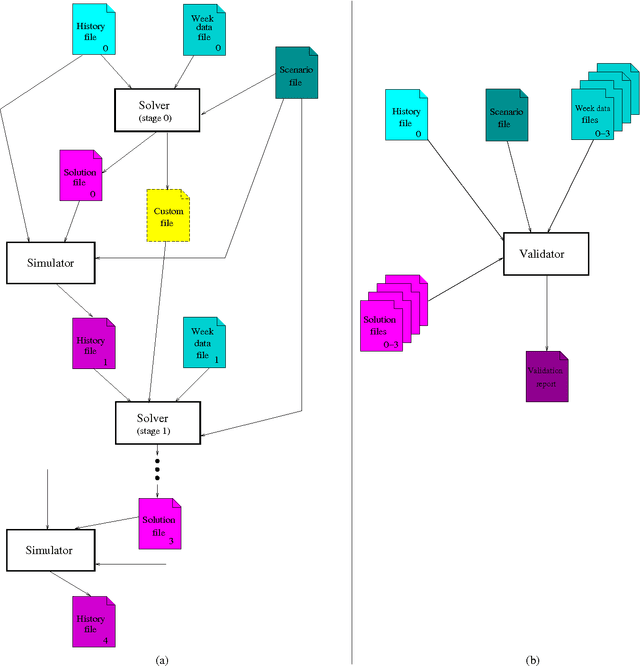
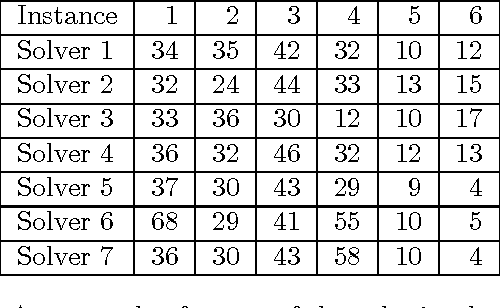
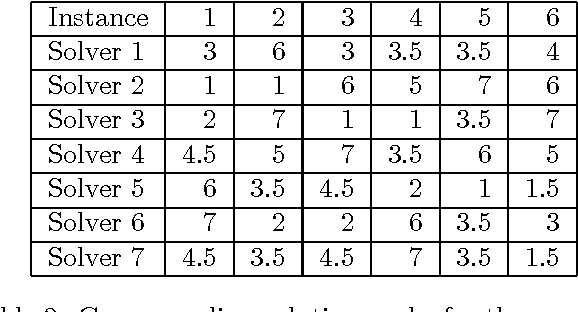
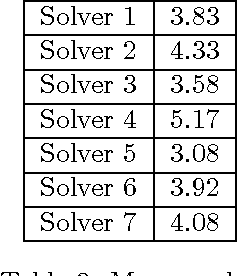
Abstract:In this paper, we provide all information to participate to the Second International Nurse Rostering Competition (INRC-II). First, we describe the problem formulation, which, differently from INRC-I, is a multi-stage procedure. Second, we illustrate all the necessary infrastructure do be used together with the participant's solver, including the testbed, the file formats, and the validation/simulation tools. Finally, we state the rules of the competition. All update-to-date information about the competition is available at http://mobiz.vives.be/inrc2/.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge