Decoupling Geometry from Optimization in 2D Irregular Cutting and Packing Problems: an Open-Source Collision Detection Engine

Addressing irregular cutting and packing (C&P) optimization problems poses two distinct challenges: the geometric challenge of determining whether or not an item can be placed feasibly at a certain position, and the optimization challenge of finding a good solution according to some objective function. Until now, those tackling such problems have had to address both challenges simultaneously, requiring two distinct sets of expertise and a lot of research & development effort. One way to lower this barrier is to decouple the two challenges. In this paper we introduce a powerful collision detection engine (CDE) for 2D irregular C&P problems which assumes full responsibility for the geometric challenge. The CDE (i) allows users to focus with full confidence on their optimization challenge by abstracting geometry away and (ii) enables independent advances to propagate to all optimization algorithms built atop it. We present a set of core principles and design philosophies to model a general and adaptable CDE focused on maximizing performance, accuracy and robustness. These principles are accompanied by a concrete open-source implementation called $\texttt{jagua-rs}$. This paper together with its implementation serves as a catalyst for future advances in irregular C&P problems by providing a solid foundation which can either be used as it currently exists or be further improved upon.

Exploring search space trees using an adapted version of Monte Carlo tree search for a combinatorial optimization problem

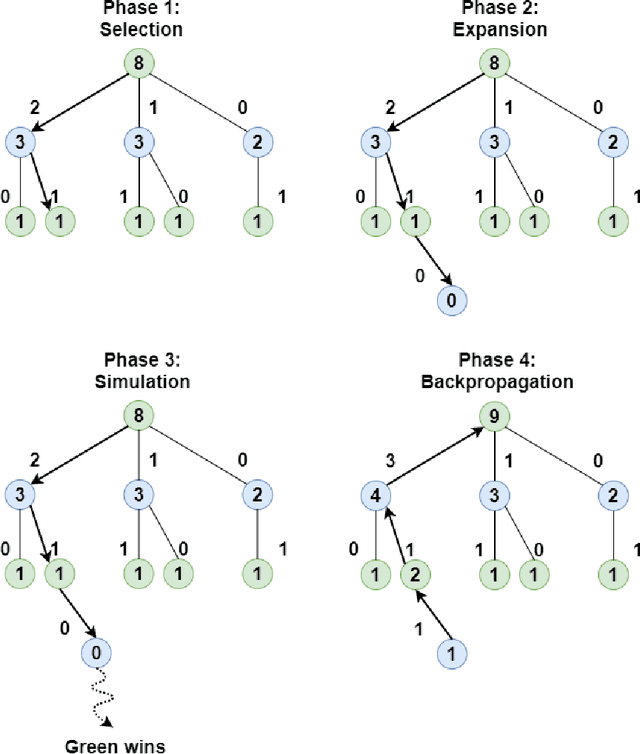
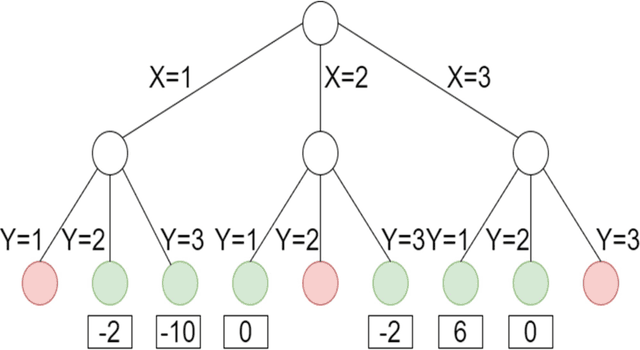
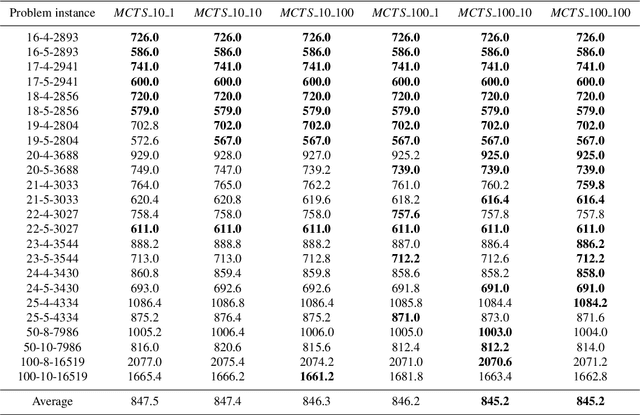
In this article, a novel approach to solve combinatorial optimization problems is proposed. This approach makes use of a heuristic algorithm to explore the search space tree of a problem instance. The algorithm is based on Monte Carlo tree search, a popular algorithm in game playing that is used to explore game trees. By leveraging the combinatorial structure of a problem, several enhancements to the algorithm are proposed. These enhancements aim to efficiently explore the search space tree by pruning subtrees, using a heuristic simulation policy, reducing the domain of variables by eliminating dominated solutions and using a beam width. They are demonstrated for a specific combinatorial optimization problem: the quay crane scheduling problem with non-crossing constraints. Computational results show that the proposed algorithm is competitive with the state-of-the-art for this problem and eight new best solutions for a benchmark set of instances are found. Apart from this, the results also show evidence that the algorithm is able to learn to correct the incorrect choices of a standard heuristic, yielding an average improvement of 10.0 % with respect to the objective function value of the solution.

Heuristics for vehicle routing problems: Sequence or set optimization?

We investigate a structural decomposition for the capacitated vehicle routing problem (CVRP) based on vehicle-to-customer "assignment" and visits "sequencing" decision variables. We show that an heuristic search focused on assignment decisions with a systematic optimal choice of sequences (using Concorde TSP solver) during each move evaluation is promising but requires a prohibitive computational effort. We therefore introduce an intermediate search space, based on the dynamic programming procedure of Balas & Simonetti, which finds a good compromise between intensification and computational efficiency. A variety of speed-up techniques are proposed for a fast exploration: neighborhood reductions, dynamic move filters, memory structures, and concatenation techniques. Finally, a tunneling strategy is designed to reshape the search space as the algorithm progresses. The combination of these techniques within a classical local search, as well as in the unified hybrid genetic search (UHGS) leads to significant improvements of solution accuracy. New best solutions are found for surprisingly small instances with as few as 256 customers. These solutions had not been attained up to now with classic neighborhoods. Overall, this research permits to better evaluate the respective impact of sequence and assignment optimization, proposes new ways of combining the optimization of these two decision sets, and opens promising research perspectives for the CVRP and its variants.