Towards net-zero manufacturing: carbon-aware scheduling for GHG emissions reduction

Detailed scheduling has traditionally been optimized for the reduction of makespan and manufacturing costs. However, growing awareness of environmental concerns and increasingly stringent regulations are pushing manufacturing towards reducing the carbon footprint of its operations. Scope 2 emissions, which are the indirect emissions related to the production and consumption of grid electricity, are in fact estimated to be responsible for more than one-third of the global GHG emissions. In this context, carbon-aware scheduling can serve as a powerful way to reduce manufacturing's carbon footprint by considering the time-dependent carbon intensity of the grid and the availability of on-site renewable electricity. This study introduces a carbon-aware permutation flow-shop scheduling model designed to reduce scope 2 emissions. The model is formulated as a mixed-integer linear problem, taking into account the forecasted grid generation mix and available on-site renewable electricity, along with the set of jobs to be scheduled and their corresponding power requirements. The objective is to find an optimal day-ahead schedule that minimizes scope 2 emissions. The problem is addressed using a dedicated memetic algorithm, combining evolutionary strategy and local search. Results from computational experiments confirm that by considering the dynamic carbon intensity of the grid and on-site renewable electricity availability, substantial reductions in carbon emissions can be achieved.

Features for the 0-1 knapsack problem based on inclusionwise maximal solutions

Decades of research on the 0-1 knapsack problem led to very efficient algorithms that are able to quickly solve large problem instances to optimality. This prompted researchers to also investigate whether relatively small problem instances exist that are hard for existing solvers and investigate which features characterize their hardness. Previously the authors proposed a new class of hard 0-1 knapsack problem instances and demonstrated that the properties of so-called inclusionwise maximal solutions (IMSs) can be important hardness indicators for this class. In the current paper, we formulate several new computationally challenging problems related to the IMSs of arbitrary 0-1 knapsack problem instances. Based on generalizations of previous work and new structural results about IMSs, we formulate polynomial and pseudopolynomial time algorithms for solving these problems. From this we derive a set of 14 computationally expensive features, which we calculate for two large datasets on a supercomputer in approximately 540 CPU-hours. We show that the proposed features contain important information related to the empirical hardness of a problem instance that was missing in earlier features from the literature by training machine learning models that can accurately predict the empirical hardness of a wide variety of 0-1 knapsack problem instances. Using the instance space analysis methodology, we also show that hard 0-1 knapsack problem instances are clustered together around a relatively dense region of the instance space and several features behave differently in the easy and hard parts of the instance space.

Exploring search space trees using an adapted version of Monte Carlo tree search for a combinatorial optimization problem

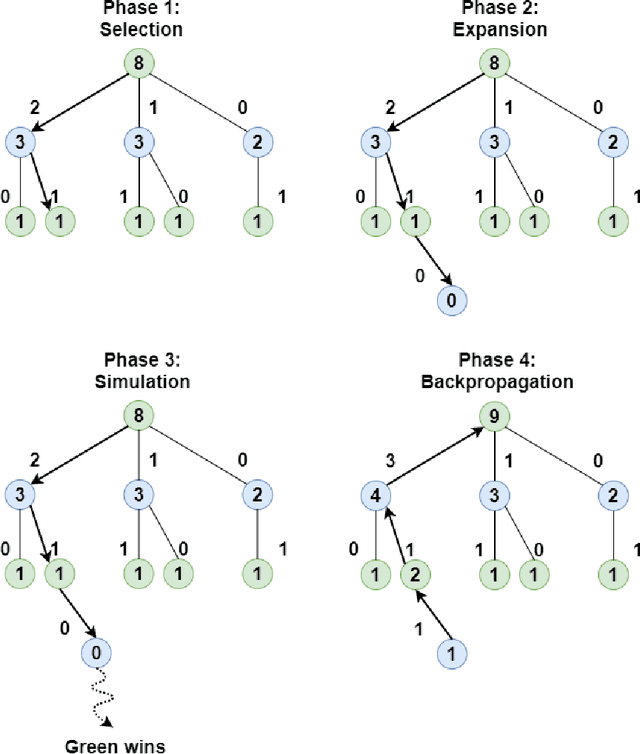
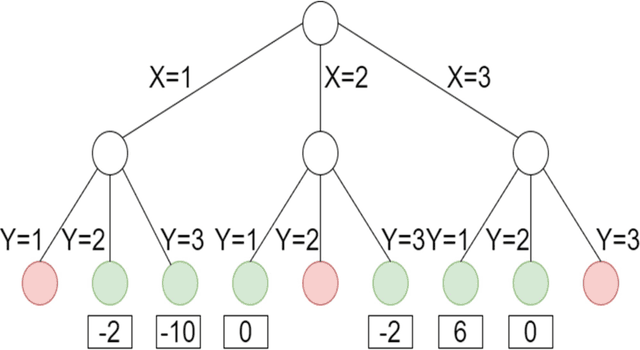
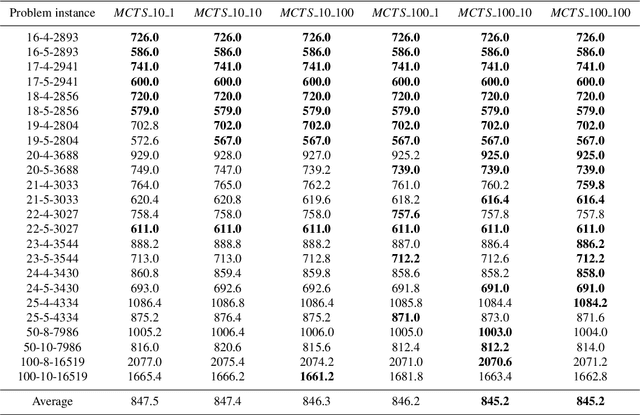
In this article, a novel approach to solve combinatorial optimization problems is proposed. This approach makes use of a heuristic algorithm to explore the search space tree of a problem instance. The algorithm is based on Monte Carlo tree search, a popular algorithm in game playing that is used to explore game trees. By leveraging the combinatorial structure of a problem, several enhancements to the algorithm are proposed. These enhancements aim to efficiently explore the search space tree by pruning subtrees, using a heuristic simulation policy, reducing the domain of variables by eliminating dominated solutions and using a beam width. They are demonstrated for a specific combinatorial optimization problem: the quay crane scheduling problem with non-crossing constraints. Computational results show that the proposed algorithm is competitive with the state-of-the-art for this problem and eight new best solutions for a benchmark set of instances are found. Apart from this, the results also show evidence that the algorithm is able to learn to correct the incorrect choices of a standard heuristic, yielding an average improvement of 10.0 % with respect to the objective function value of the solution.