Exact and Heuristic Approaches to Drone Delivery Problems

The Flying Sidekick Traveling Salesman Problem (FSTSP) considers a delivery system composed by a truck and a drone. The drone launches from the truck with a single package to deliver to a customer. Each drone must return to the truck to recharge batteries, pick up another package, and launch again to a new customer location. This work proposes a novel Mixed Integer Programming (MIP) formulation and a heuristic approach to address the problem. The proposedMIP formulation yields better linear relaxation bounds than previously proposed formulations for all instances, and was capable of optimally solving several unsolved instances from the literature. A hybrid heuristic based on the General Variable Neighborhood Search metaheuristic combining Tabu Search concepts is employed to obtain high-quality solutions for large-size instances. The efficiency of the algorithm was evaluated on 1415 benchmark instances from the literature, and over 80% of the best known solutions were improved.

The double traveling salesman problem with partial last-in-first-out loading constraints

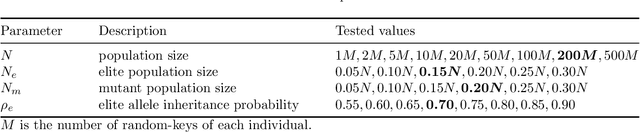
In this paper, we introduce the Double Traveling Salesman Problem with Partial Last-In-First-Out Loading Constraints (DTSPPL), a pickup-and-delivery single-vehicle routing problem where all pickup operations must be performed before any delivery one because the pickup and delivery areas are geographically separated. The vehicle collects items in the pickup area and loads them into its container, a horizontal stack. After performing all pickup operations, the vehicle begins delivering the items in the delivery area. Loading and unloading operations must obey a partial Last-In-First-Out (LIFO) policy, i.e., a version of the LIFO policy that may be violated within a given reloading depth. The objective of the DTSPPL is to minimize the total cost, which involves the total distance traveled by the vehicle and the number of reloaded items due to violations of the standard LIFO policy. We formally describe the DTSPPL by means of two Integer Linear Programming (ILP) formulations, and propose a heuristic algorithm based on the Biased Random-Key Genetic Algorithm (BRKGA) to find high-quality solutions. The performance of the proposed solution approaches is assessed over a broad set of instances. Computational results have shown that both ILP formulations were able to solve only the smaller instances, whereas the BRKGA obtained better solutions for almost all instances, requiring shorter computational time.

Heuristics for vehicle routing problems: Sequence or set optimization?

We investigate a structural decomposition for the capacitated vehicle routing problem (CVRP) based on vehicle-to-customer "assignment" and visits "sequencing" decision variables. We show that an heuristic search focused on assignment decisions with a systematic optimal choice of sequences (using Concorde TSP solver) during each move evaluation is promising but requires a prohibitive computational effort. We therefore introduce an intermediate search space, based on the dynamic programming procedure of Balas & Simonetti, which finds a good compromise between intensification and computational efficiency. A variety of speed-up techniques are proposed for a fast exploration: neighborhood reductions, dynamic move filters, memory structures, and concatenation techniques. Finally, a tunneling strategy is designed to reshape the search space as the algorithm progresses. The combination of these techniques within a classical local search, as well as in the unified hybrid genetic search (UHGS) leads to significant improvements of solution accuracy. New best solutions are found for surprisingly small instances with as few as 256 customers. These solutions had not been attained up to now with classic neighborhoods. Overall, this research permits to better evaluate the respective impact of sequence and assignment optimization, proposes new ways of combining the optimization of these two decision sets, and opens promising research perspectives for the CVRP and its variants.