A Non-Dominated Sorting Based Customized Random-Key Genetic Algorithm for the Bi-Objective Traveling Thief Problem

In this paper, we propose a method to solve a bi-objective variant of the well-studied Traveling Thief Problem (TTP). The TTP is a multi-component problem that combines two classic combinatorial problems: Traveling Salesman Problem (TSP) and Knapsack Problem (KP). In the TTP, a thief has to visit each city exactly once and can pick items throughout their journey. The thief begins their journey with an empty knapsack and travels with a speed inversely proportional to the knapsack weight. We address the BI-TTP, a bi-objective version of the TTP, where the goal is to minimize the overall traveling time and to maximize the profit of the collected items. Our method is based on a genetic algorithm with customization addressing problem characteristics. We incorporate domain knowledge through a combination of near-optimal solutions of each subproblem in the initial population and a custom repair operation to avoid the evaluation of infeasible solutions. Moreover, the independent variables of the TSP and KP components are unified to a real variable representation by using a biased random-key approach. The bi-objective aspect of the problem is addressed through an elite population extracted based on the non-dominated rank and crowding distance of each solution. Furthermore, we provide a comprehensive study which shows the influence of hyperparameters on the performance of our method and investigate the performance of each hyperparameter combination over time. In addition to our experiments, we discuss the results of the BI-TTP competitions at EMO-2019 and GECCO-2019 conferences where our method has won first and second place, respectively, thus proving its ability to find high-quality solutions consistently.

The double traveling salesman problem with partial last-in-first-out loading constraints

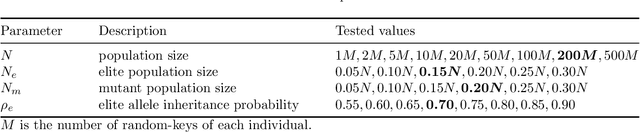
In this paper, we introduce the Double Traveling Salesman Problem with Partial Last-In-First-Out Loading Constraints (DTSPPL), a pickup-and-delivery single-vehicle routing problem where all pickup operations must be performed before any delivery one because the pickup and delivery areas are geographically separated. The vehicle collects items in the pickup area and loads them into its container, a horizontal stack. After performing all pickup operations, the vehicle begins delivering the items in the delivery area. Loading and unloading operations must obey a partial Last-In-First-Out (LIFO) policy, i.e., a version of the LIFO policy that may be violated within a given reloading depth. The objective of the DTSPPL is to minimize the total cost, which involves the total distance traveled by the vehicle and the number of reloaded items due to violations of the standard LIFO policy. We formally describe the DTSPPL by means of two Integer Linear Programming (ILP) formulations, and propose a heuristic algorithm based on the Biased Random-Key Genetic Algorithm (BRKGA) to find high-quality solutions. The performance of the proposed solution approaches is assessed over a broad set of instances. Computational results have shown that both ILP formulations were able to solve only the smaller instances, whereas the BRKGA obtained better solutions for almost all instances, requiring shorter computational time.