The double traveling salesman problem with partial last-in-first-out loading constraints

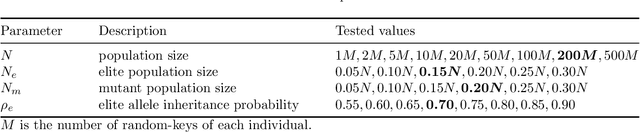
In this paper, we introduce the Double Traveling Salesman Problem with Partial Last-In-First-Out Loading Constraints (DTSPPL), a pickup-and-delivery single-vehicle routing problem where all pickup operations must be performed before any delivery one because the pickup and delivery areas are geographically separated. The vehicle collects items in the pickup area and loads them into its container, a horizontal stack. After performing all pickup operations, the vehicle begins delivering the items in the delivery area. Loading and unloading operations must obey a partial Last-In-First-Out (LIFO) policy, i.e., a version of the LIFO policy that may be violated within a given reloading depth. The objective of the DTSPPL is to minimize the total cost, which involves the total distance traveled by the vehicle and the number of reloaded items due to violations of the standard LIFO policy. We formally describe the DTSPPL by means of two Integer Linear Programming (ILP) formulations, and propose a heuristic algorithm based on the Biased Random-Key Genetic Algorithm (BRKGA) to find high-quality solutions. The performance of the proposed solution approaches is assessed over a broad set of instances. Computational results have shown that both ILP formulations were able to solve only the smaller instances, whereas the BRKGA obtained better solutions for almost all instances, requiring shorter computational time.

A heuristic algorithm for a single vehicle static bike sharing rebalancing problem

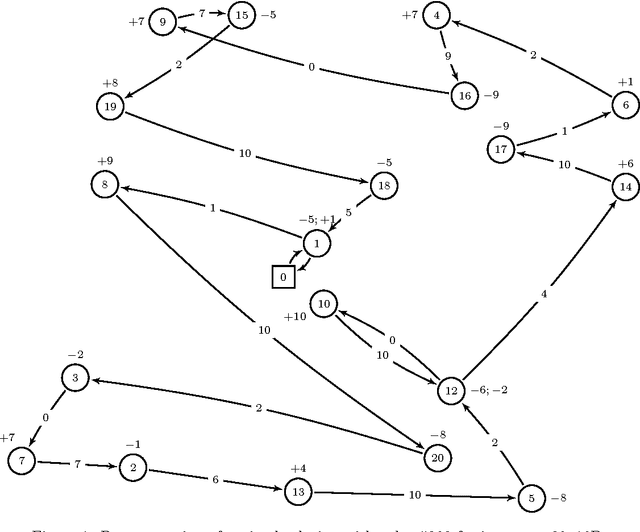
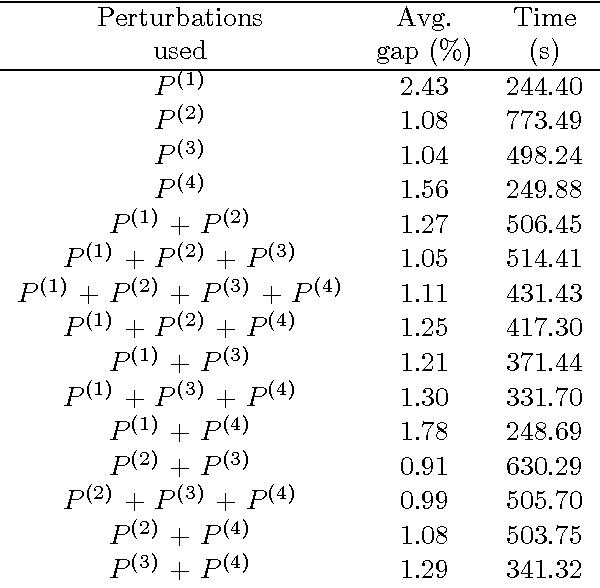
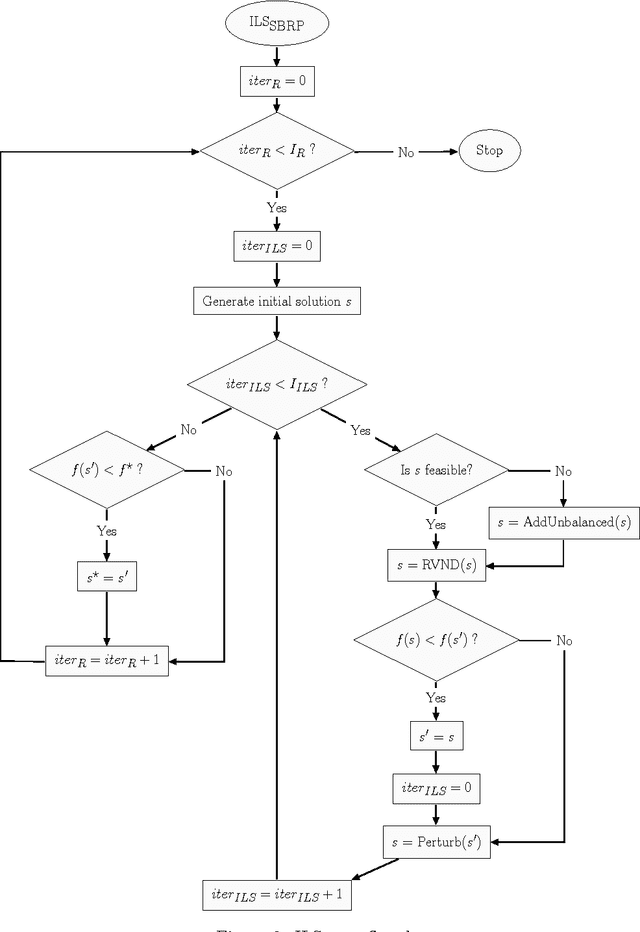
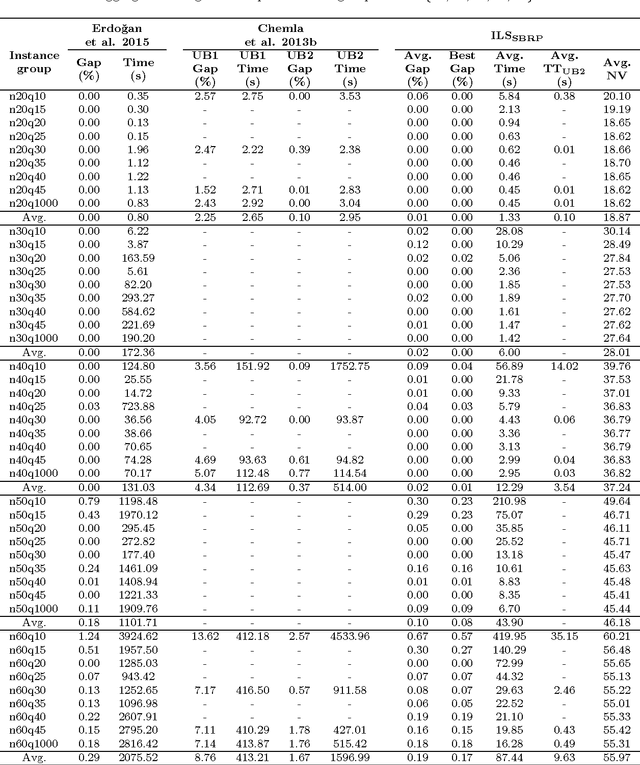
The static bike rebalancing problem (SBRP) concerns the task of repositioning bikes among stations in self-service bike-sharing systems. This problem can be seen as a variant of the one-commodity pickup and delivery vehicle routing problem, where multiple visits are allowed to be performed at each station, i.e., the demand of a station is allowed to be split. Moreover, a vehicle may temporarily drop its load at a station, leaving it in excess or, alternatively, collect more bikes from a station (even all of them), thus leaving it in default. Both cases require further visits in order to meet the actual demands of such station. This paper deals with a particular case of the SBRP, in which only a single vehicle is available and the objective is to find a least-cost route that meets the demand of all stations and does not violate the minimum (zero) and maximum (vehicle capacity) load limits along the tour. Therefore, the number of bikes to be collected or delivered at each station should be appropriately determined in order to respect such constraints. We propose an iterated local search (ILS) based heuristic to solve the problem. The ILS algorithm was tested on 980 benchmark instances from the literature and the results obtained are quite competitive when compared to other existing methods. Moreover, our heuristic was capable of finding most of the known optimal solutions and also of improving the results on a number of open instances.