A prediction-based approach for online dynamic radiotherapy scheduling

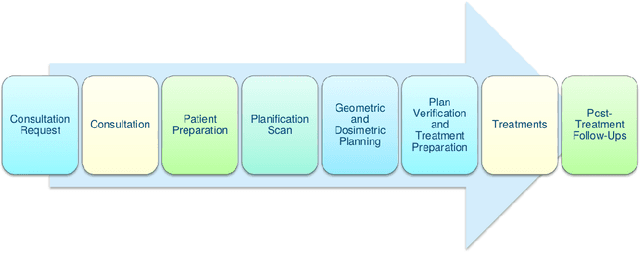
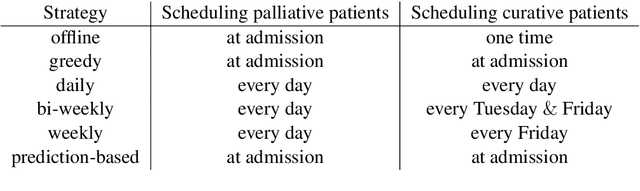
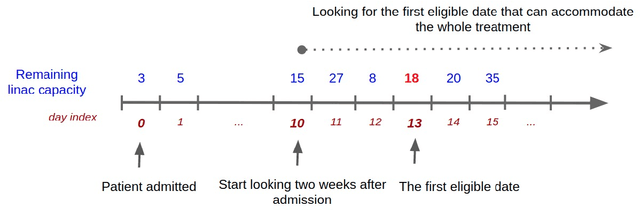
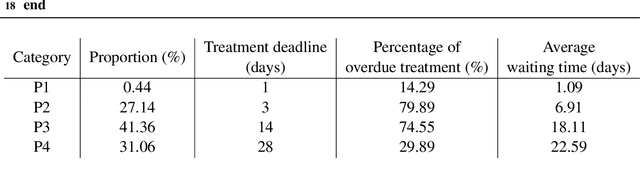
Patient scheduling is a difficult task as it involves dealing with stochastic factors such as an unknown arrival flow of patients. Scheduling radiotherapy treatments for cancer patients faces a similar problem. Curative patients need to start their treatment within the recommended deadlines, i.e., 14 or 28 days after their admission while reserving treatment capacity for palliative patients who require urgent treatments within 1 to 3 days after their admission. Most cancer centers solve the problem by reserving a fixed number of treatment slots for emergency patients. However, this flat-reservation approach is not ideal and can cause overdue treatments for emergency patients on some days while not fully exploiting treatment capacity on some other days, which also leads to delaying treatment for curative patients. This problem is especially severe in large and crowded hospitals. In this paper, we propose a prediction-based approach for online dynamic radiotherapy scheduling. An offline problem where all future patient arrivals are known in advance is solved to optimality using Integer Programming. A regression model is then trained to recognize the links between patients' arrival patterns and their ideal waiting time. The trained regression model is then embedded in a prediction-based approach that schedules a patient based on their characteristics and the present state of the calendar. The numerical results show that our prediction-based approach efficiently prevents overdue treatments for emergency patients while maintaining a good waiting time compared to other scheduling approaches based on a flat-reservation policy.

The Commute Trip Sharing Problem

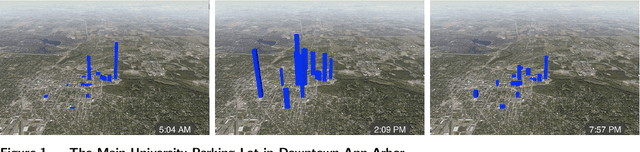
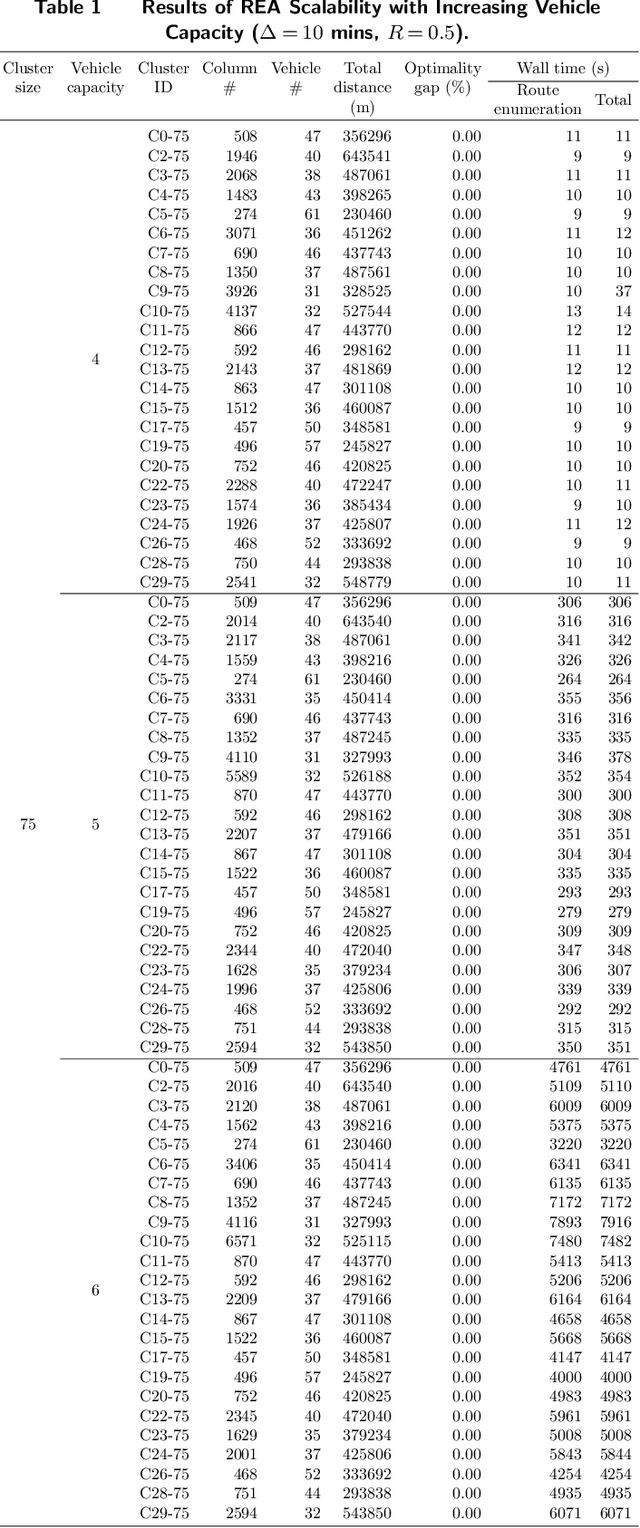
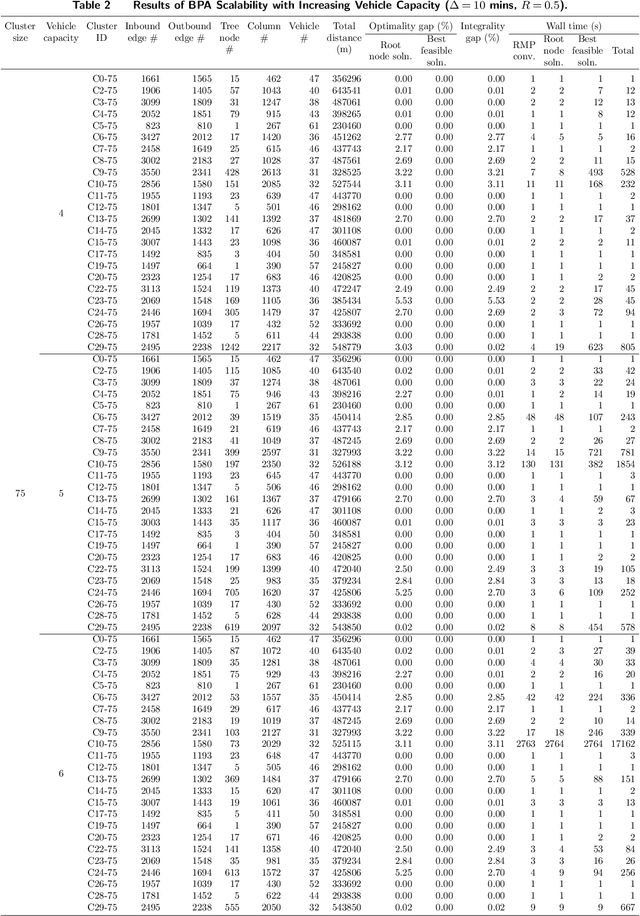
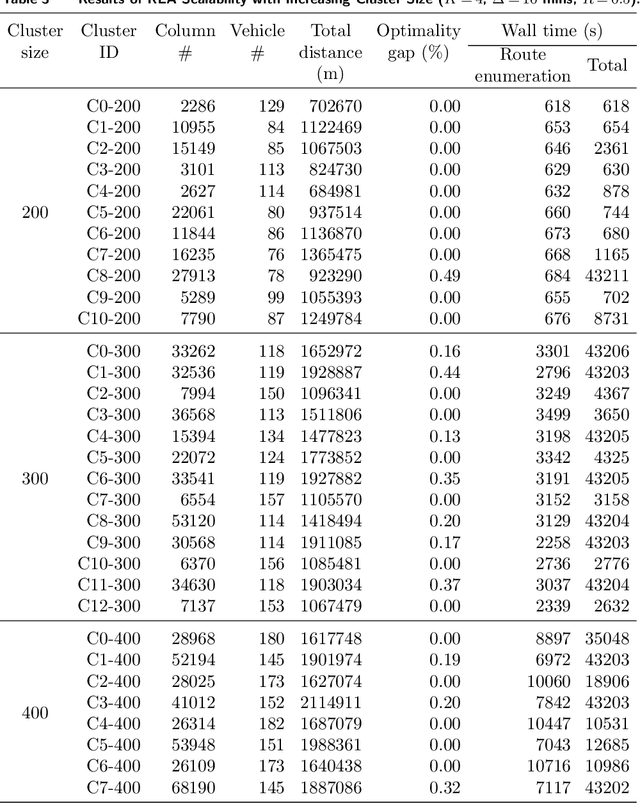
Parking pressure has been steadily increasing in cities as well as in university and corporate campuses. To relieve this pressure, this paper studies a car-pooling platform that would match riders and drivers, while guaranteeing a ride back and exploiting spatial and temporal locality. In particular, the paper formalizes the Commute Trip Sharing Problem (CTSP) to find a routing plan that maximizes ride sharing for a set of commute trips. The CTSP is a generalization of the vehicle routing problem with routes that satisfy time window, capacity, pairing, precedence, ride duration, and driver constraints. The paper introduces two exact algorithms for the CTPS: A route-enumeration algorithm and a branch-and-price algorithm. Experimental results show that, on a high-fidelity, real-world dataset of commute trips from a mid-size city, both algorithms optimally solve small and medium-sized problems and produce high-quality solutions for larger problem instances. The results show that car pooling, if widely adopted, has the potential to reduce vehicle usage by up to 57% and decrease vehicle miles traveled by up to 46% while only incurring a 22% increase in average ride time per commuter for the trips considered.