Learning Valid Dual Bounds in Constraint Programming: Boosted Lagrangian Decomposition with Self-Supervised Learning

Lagrangian decomposition (LD) is a relaxation method that provides a dual bound for constrained optimization problems by decomposing them into more manageable sub-problems. This bound can be used in branch-and-bound algorithms to prune the search space effectively. In brief, a vector of Lagrangian multipliers is associated with each sub-problem, and an iterative procedure (e.g., a sub-gradient optimization) adjusts these multipliers to find the tightest bound. Initially applied to integer programming, Lagrangian decomposition also had success in constraint programming due to its versatility and the fact that global constraints provide natural sub-problems. However, the non-linear and combinatorial nature of sub-problems in constraint programming makes it computationally intensive to optimize the Lagrangian multipliers with sub-gradient methods at each node of the tree search. This currently limits the practicality of LD as a general bounding mechanism for constraint programming. To address this challenge, we propose a self-supervised learning approach that leverages neural networks to generate multipliers directly, yielding tight bounds. This approach significantly reduces the number of sub-gradient optimization steps required, enhancing the pruning efficiency and reducing the execution time of constraint programming solvers. This contribution is one of the few that leverage learning to enhance bounding mechanisms on the dual side, a critical element in the design of combinatorial solvers. To our knowledge, this work presents the first generic method for learning valid dual bounds in constraint programming.

Learning Lagrangian Multipliers for the Travelling Salesman Problem

Lagrangian relaxation is a versatile mathematical technique employed to relax constraints in an optimization problem, enabling the generation of dual bounds to prove the optimality of feasible solutions and the design of efficient propagators in constraint programming (such as the weighted circuit constraint). However, the conventional process of deriving Lagrangian multipliers (e.g., using subgradient methods) is often computationally intensive, limiting its practicality for large-scale or time-sensitive problems. To address this challenge, we propose an innovative unsupervised learning approach that harnesses the capabilities of graph neural networks to exploit the problem structure, aiming to generate accurate Lagrangian multipliers efficiently. We apply this technique to the well-known Held-Karp Lagrangian relaxation for the travelling salesman problem. The core idea is to predict accurate Lagrangian multipliers and to employ them as a warm start for generating Held-Karp relaxation bounds. These bounds are subsequently utilized to enhance the filtering process carried out by branch-and-bound algorithms. In contrast to much of the existing literature, which primarily focuses on finding feasible solutions, our approach operates on the dual side, demonstrating that learning can also accelerate the proof of optimality. We conduct experiments across various distributions of the metric travelling salesman problem, considering instances with up to 200 cities. The results illustrate that our approach can improve the filtering level of the weighted circuit global constraint, reduce the optimality gap by a factor two for unsolved instances up to a timeout, and reduce the execution time for solved instances by 10%.

Training a Deep Q-Learning Agent Inside a Generic Constraint Programming Solver

Constraint programming is known for being an efficient approach for solving combinatorial problems. Important design choices in a solver are the branching heuristics, which are designed to lead the search to the best solutions in a minimum amount of time. However, developing these heuristics is a time-consuming process that requires problem-specific expertise. This observation has motivated many efforts to use machine learning to automatically learn efficient heuristics without expert intervention. To the best of our knowledge, it is still an open research question. Although several generic variable-selection heuristics are available in the literature, the options for a generic value-selection heuristic are more scarce. In this paper, we propose to tackle this issue by introducing a generic learning procedure that can be used to obtain a value-selection heuristic inside a constraint programming solver. This has been achieved thanks to the combination of a deep Q-learning algorithm, a tailored reward signal, and a heterogeneous graph neural network architecture. Experiments on graph coloring, maximum independent set, and maximum cut problems show that our framework is able to find better solutions close to optimality without requiring a large amounts of backtracks while being generic.

A prediction-based approach for online dynamic radiotherapy scheduling

Patient scheduling is a difficult task as it involves dealing with stochastic factors such as an unknown arrival flow of patients. Scheduling radiotherapy treatments for cancer patients faces a similar problem. Curative patients need to start their treatment within the recommended deadlines, i.e., 14 or 28 days after their admission while reserving treatment capacity for palliative patients who require urgent treatments within 1 to 3 days after their admission. Most cancer centers solve the problem by reserving a fixed number of treatment slots for emergency patients. However, this flat-reservation approach is not ideal and can cause overdue treatments for emergency patients on some days while not fully exploiting treatment capacity on some other days, which also leads to delaying treatment for curative patients. This problem is especially severe in large and crowded hospitals. In this paper, we propose a prediction-based approach for online dynamic radiotherapy scheduling. An offline problem where all future patient arrivals are known in advance is solved to optimality using Integer Programming. A regression model is then trained to recognize the links between patients' arrival patterns and their ideal waiting time. The trained regression model is then embedded in a prediction-based approach that schedules a patient based on their characteristics and the present state of the calendar. The numerical results show that our prediction-based approach efficiently prevents overdue treatments for emergency patients while maintaining a good waiting time compared to other scheduling approaches based on a flat-reservation policy.

Supervised learning and tree search for real-time storage allocation in Robotic Mobile Fulfillment Systems

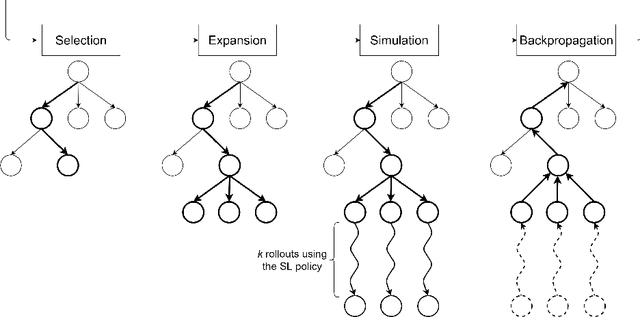
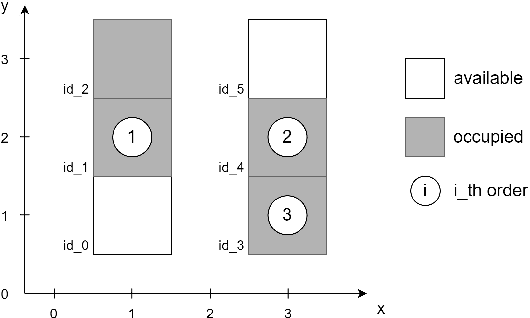
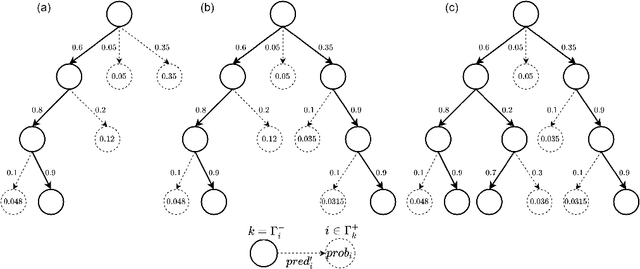
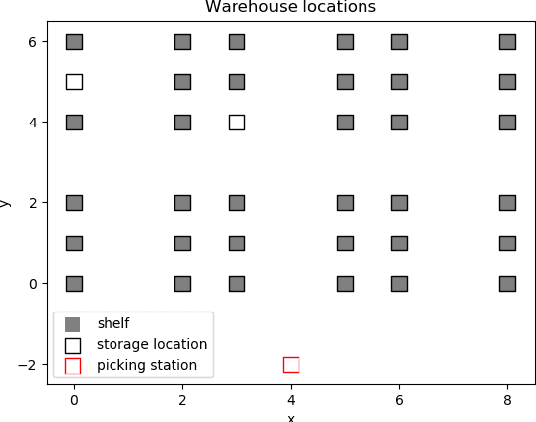
A Robotic Mobile Fulfillment System is a robotised parts-to-picker system that is particularly well-suited for e-commerce warehousing. One distinguishing feature of this type of warehouse is its high storage modularity. Numerous robots are moving shelves simultaneously, and the shelves can be returned to any open location after the picking operation is completed. This work focuses on the real-time storage allocation problem to minimise the travel time of the robots. An efficient -- but computationally costly -- Monte Carlo Tree Search method is used offline to generate high-quality experience. This experience can be learned by a neural network with a proper coordinates-based features representation. The obtained neural network is used as an action predictor in several new storage policies, either as-is or in rollout and supervised tree search strategies. Resulting performance levels depend on the computing time available at a decision step and are consistently better compared to real-time decision rules from the literature.

SeaPearl: A Constraint Programming Solver guided by Reinforcement Learning

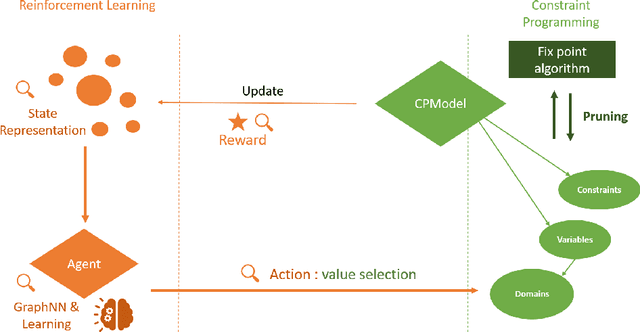
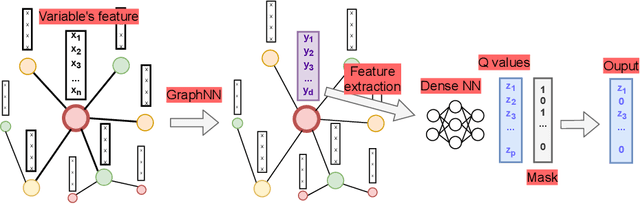
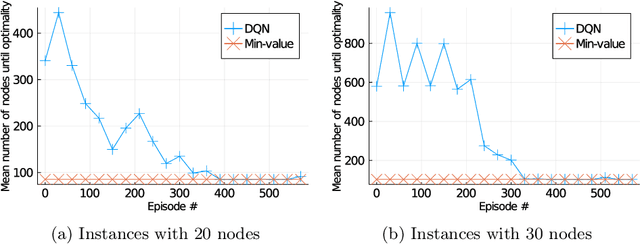
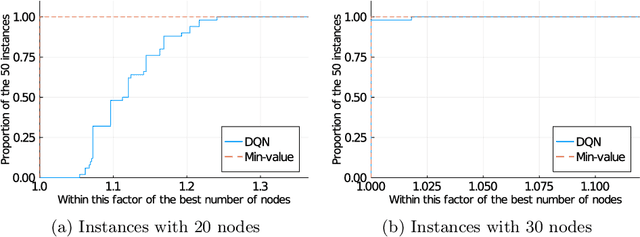
The design of efficient and generic algorithms for solving combinatorial optimization problems has been an active field of research for many years. Standard exact solving approaches are based on a clever and complete enumeration of the solution set. A critical and non-trivial design choice with such methods is the branching strategy, directing how the search is performed. The last decade has shown an increasing interest in the design of machine learning-based heuristics to solve combinatorial optimization problems. The goal is to leverage knowledge from historical data to solve similar new instances of a problem. Used alone, such heuristics are only able to provide approximate solutions efficiently, but cannot prove optimality nor bounds on their solution. Recent works have shown that reinforcement learning can be successfully used for driving the search phase of constraint programming (CP) solvers. However, it has also been shown that this hybridization is challenging to build, as standard CP frameworks do not natively include machine learning mechanisms, leading to some sources of inefficiencies. This paper presents the proof of concept for SeaPearl, a new CP solver implemented in Julia, that supports machine learning routines in order to learn branching decisions using reinforcement learning. Support for modeling the learning component is also provided. We illustrate the modeling and solution performance of this new solver on two problems. Although not yet competitive with industrial solvers, SeaPearl aims to provide a flexible and open-source framework in order to facilitate future research in the hybridization of constraint programming and machine learning.

Predicting the probability distribution of bus travel time to move towards reliable planning of public transport services

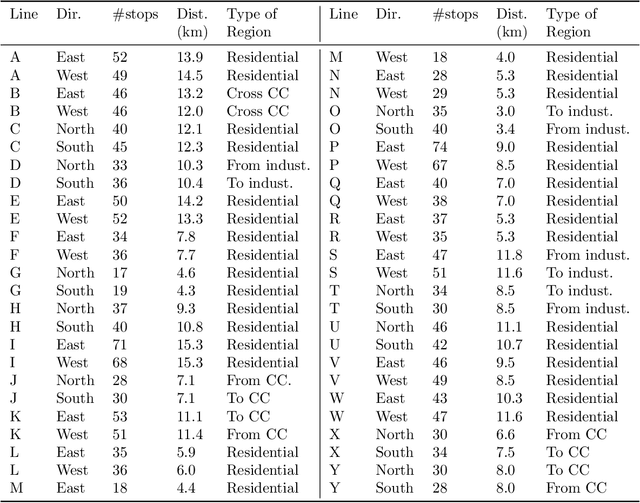
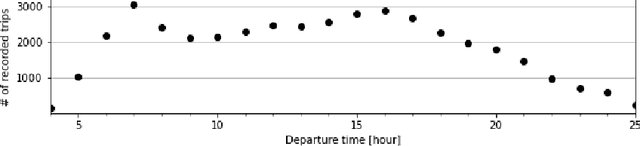
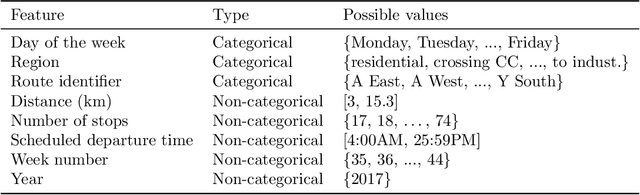
An important aspect of the quality of a public transport service is its reliability, which is defined as the invariability of the service attributes. Preventive measures taken during planning can reduce risks of unreliability throughout operations. In order to tackle reliability during the service planning phase, a key piece of information is the long-term prediction of the density of the travel time, which conveys the uncertainty of travel times. We introduce a reliable approach to one of the problems of service planning in public transport, namely the Multiple Depot Vehicle Scheduling Problem (MDVSP), which takes as input a set of trips and the probability density function (p.d.f.) of the travel time of each trip in order to output delay-tolerant vehicle schedules. This work empirically compares probabilistic models for the prediction of the conditional p.d.f. of the travel time, as a first step towards reliable MDVSP solutions. Two types of probabilistic models, namely similarity-based density estimation models and a smoothed Logistic Regression for probabilistic classification model, are compared on a dataset of more than 41,000 trips and 50 bus routes of the city of Montr\'eal. The result of a vast majority of probabilistic models outperforms that of a Random Forests model, which is not inherently probabilistic, thus highlighting the added value of modeling the conditional p.d.f. of the travel time with probabilistic models. A similarity-based density estimation model using a $k$ Nearest Neighbors method and a Kernel Density Estimation predicted the best estimate of the true conditional p.d.f. on this dataset.

E-commerce warehousing: learning a storage policy

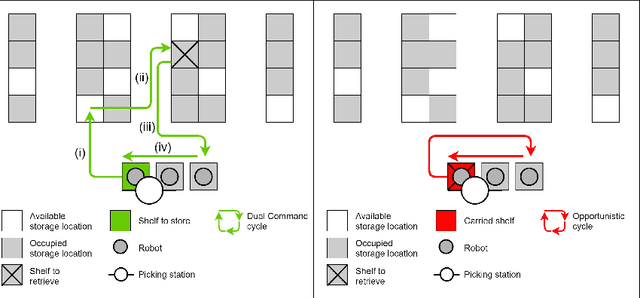
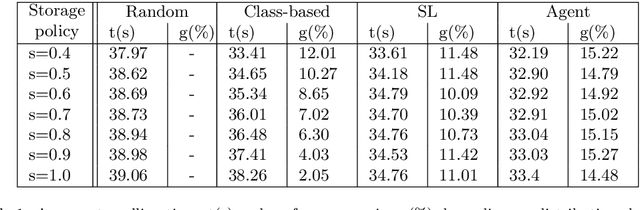
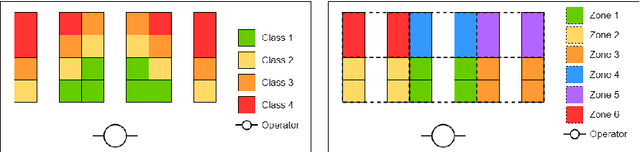
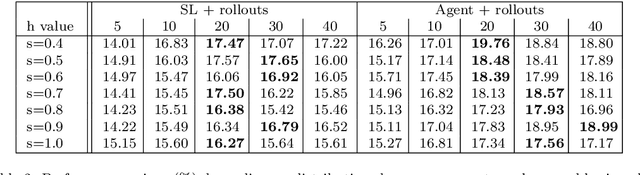
E-commerce with major online retailers is changing the way people consume. The goal of increasing delivery speed while remaining cost-effective poses significant new challenges for supply chains as they race to satisfy the growing and fast-changing demand. In this paper, we consider a warehouse with a Robotic Mobile Fulfillment System (RMFS), in which a fleet of robots stores and retrieves shelves of items and brings them to human pickers. To adapt to changing demand, uncertainty, and differentiated service (e.g., prime vs. regular), one can dynamically modify the storage allocation of a shelf. The objective is to define a dynamic storage policy to minimise the average cycle time used by the robots to fulfil requests. We propose formulating this system as a Partially Observable Markov Decision Process, and using a Deep Q-learning agent from Reinforcement Learning, to learn an efficient real-time storage policy that leverages repeated experiences and insightful forecasts using simulations. Additionally, we develop a rollout strategy to enhance our method by leveraging more information available at a given time step. Using simulations to compare our method to traditional storage rules used in the industry showed preliminary results up to 14\% better in terms of travelling times.

Learning TSP Requires Rethinking Generalization

End-to-end training of neural network solvers for combinatorial problems such as the Travelling Salesman Problem is intractable and inefficient beyond a few hundreds of nodes. While state-of-the-art Machine Learning approaches perform closely to classical solvers for trivially small sizes, they are unable to generalize the learnt policy to larger instances of practical scales. Towards leveraging transfer learning to solve large-scale TSPs, this paper identifies inductive biases, model architectures and learning algorithms that promote generalization to instances larger than those seen in training. Our controlled experiments provide the first principled investigation into such zero-shot generalization, revealing that extrapolating beyond training data requires rethinking the entire neural combinatorial optimization pipeline, from network layers and learning paradigms to evaluation protocols.

Combining Reinforcement Learning and Constraint Programming for Combinatorial Optimization

Combinatorial optimization has found applications in numerous fields, from aerospace to transportation planning and economics. The goal is to find an optimal solution among a finite set of possibilities. The well-known challenge one faces with combinatorial optimization is the state-space explosion problem: the number of possibilities grows exponentially with the problem size, which makes solving intractable for large problems. In the last years, deep reinforcement learning (DRL) has shown its promise for designing good heuristics dedicated to solve NP-hard combinatorial optimization problems. However, current approaches have two shortcomings: (1) they mainly focus on the standard travelling salesman problem and they cannot be easily extended to other problems, and (2) they only provide an approximate solution with no systematic ways to improve it or to prove optimality. In another context, constraint programming (CP) is a generic tool to solve combinatorial optimization problems. Based on a complete search procedure, it will always find the optimal solution if we allow an execution time large enough. A critical design choice, that makes CP non-trivial to use in practice, is the branching decision, directing how the search space is explored. In this work, we propose a general and hybrid approach, based on DRL and CP, for solving combinatorial optimization problems. The core of our approach is based on a dynamic programming formulation, that acts as a bridge between both techniques. We experimentally show that our solver is efficient to solve two challenging problems: the traveling salesman problem with time windows, and the 4-moments portfolio optimization problem. Results obtained show that the framework introduced outperforms the stand-alone RL and CP solutions, while being competitive with industrial solvers.