Andrea Lodi
GPU-friendly and Linearly Convergent First-order Methods for Certifying Optimal $k$-sparse GLMs
Mar 01, 2026Abstract:We investigate the problem of certifying optimality for sparse generalized linear models (GLMs), where sparsity is enforced through a cardinality constraint. While Branch-and-Bound (BnB) frameworks can certify optimality using perspective relaxations, existing methods for solving these relaxations are computationally intensive, limiting their scalability. To address this challenge, we reformulate the relaxations as composite optimization problems and develop a unified proximal framework that is both linearly convergent and computationally efficient. Under specific geometric regularity conditions, our analysis links primal quadratic growth to dual quadratic decay, yielding error bounds that make the Fenchel duality gap a sharp proxy for progress towards the solution set. This leads to a duality gap-based restart scheme that upgrades a broad class of sublinear proximal methods to provably linearly convergent methods, and applies beyond the sparse GLM setting. For the implicit perspective regularizer, we further derive specialized routines to evaluate the regularizer and its proximal operator exactly in log-linear time, avoiding costly generic conic solvers. The resulting iterations are dominated by matrix--vector multiplications, which enables GPU acceleration. Experiments on synthetic and real-world datasets show orders-of-magnitude faster dual-bound computations and substantially improved BnB scalability on large instances.
Batched First-Order Methods for Parallel LP Solving in MIP
Jan 29, 2026Abstract:We present a batched first-order method for solving multiple linear programs in parallel on GPUs. Our approach extends the primal-dual hybrid gradient algorithm to efficiently solve batches of related linear programming problems that arise in mixed-integer programming techniques such as strong branching and bound tightening. By leveraging matrix-matrix operations instead of repeated matrix-vector operations, we obtain significant computational advantages on GPU architectures. We demonstrate the effectiveness of our approach on various case studies and identify the problem sizes where first-order methods outperform traditional simplex-based solvers depending on the computational environment one can use. This is a significant step for the design and development of integer programming algorithms tightly exploiting GPU capabilities where we argue that some specific operations should be allocated to GPUs and performed in full instead of using light-weight heuristic approaches on CPUs.
SMiLE: Provably Enforcing Global Relational Properties in Neural Networks
Nov 10, 2025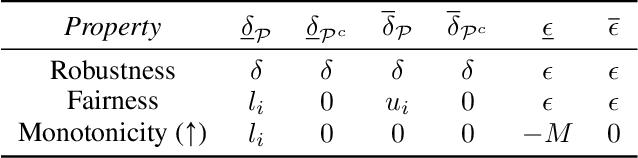
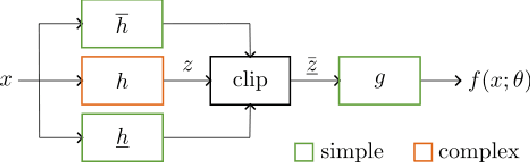
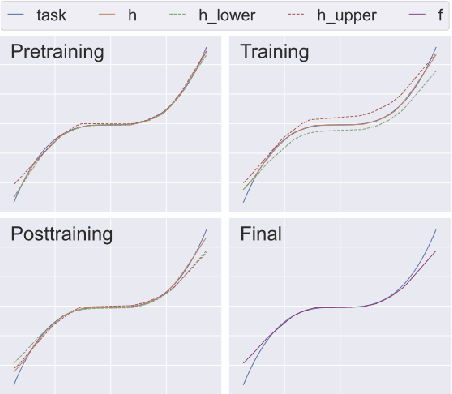
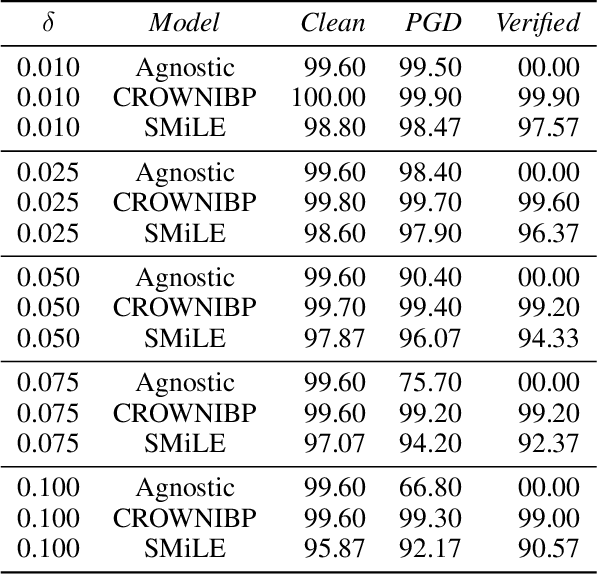
Abstract:Artificial Intelligence systems are increasingly deployed in settings where ensuring robustness, fairness, or domain-specific properties is essential for regulation compliance and alignment with human values. However, especially on Neural Networks, property enforcement is very challenging, and existing methods are limited to specific constraints or local properties (defined around datapoints), or fail to provide full guarantees. We tackle these limitations by extending SMiLE, a recently proposed enforcement framework for NNs, to support global relational properties (defined over the entire input space). The proposed approach scales well with model complexity, accommodates general properties and backbones, and provides full satisfaction guarantees. We evaluate SMiLE on monotonicity, global robustness, and individual fairness, on synthetic and real data, for regression and classification tasks. Our approach is competitive with property-specific baselines in terms of accuracy and runtime, and strictly superior in terms of generality and level of guarantees. Overall, our results emphasize the potential of the SMiLE framework as a platform for future research and applications.
Scalable First-order Method for Certifying Optimal k-Sparse GLMs
Feb 13, 2025Abstract:This paper investigates the problem of certifying optimality for sparse generalized linear models (GLMs), where sparsity is enforced through an $\ell_0$ cardinality constraint. While branch-and-bound (BnB) frameworks can certify optimality by pruning nodes using dual bounds, existing methods for computing these bounds are either computationally intensive or exhibit slow convergence, limiting their scalability to large-scale problems. To address this challenge, we propose a first-order proximal gradient algorithm designed to solve the perspective relaxation of the problem within a BnB framework. Specifically, we formulate the relaxed problem as a composite optimization problem and demonstrate that the proximal operator of the non-smooth component can be computed exactly in log-linear time complexity, eliminating the need to solve a computationally expensive second-order cone program. Furthermore, we introduce a simple restart strategy that enhances convergence speed while maintaining low per-iteration complexity. Extensive experiments on synthetic and real-world datasets show that our approach significantly accelerates dual bound computations and is highly effective in providing optimality certificates for large-scale problems.
The Differentiable Feasibility Pump
Nov 05, 2024



Abstract:Although nearly 20 years have passed since its conception, the feasibility pump algorithm remains a widely used heuristic to find feasible primal solutions to mixed-integer linear problems. Many extensions of the initial algorithm have been proposed. Yet, its core algorithm remains centered around two key steps: solving the linear relaxation of the original problem to obtain a solution that respects the constraints, and rounding it to obtain an integer solution. This paper shows that the traditional feasibility pump and many of its follow-ups can be seen as gradient-descent algorithms with specific parameters. A central aspect of this reinterpretation is observing that the traditional algorithm differentiates the solution of the linear relaxation with respect to its cost. This reinterpretation opens many opportunities for improving the performance of the original algorithm. We study how to modify the gradient-update step as well as extending its loss function. We perform extensive experiments on MIPLIB instances and show that these modifications can substantially reduce the number of iterations needed to find a solution.
Dual Policy Reinforcement Learning for Real-time Rebalancing in Bike-sharing Systems
Jun 02, 2024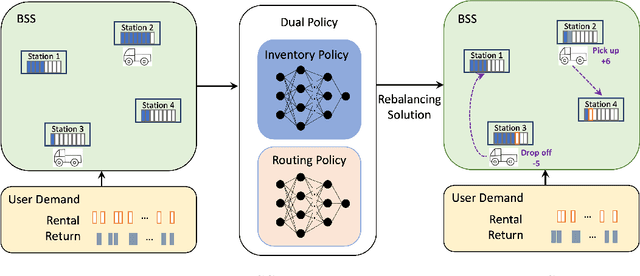


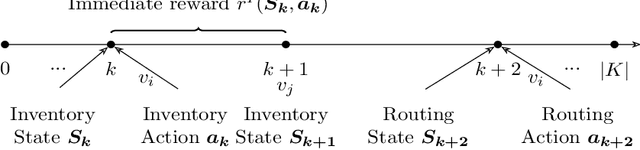
Abstract:Bike-sharing systems play a crucial role in easing traffic congestion and promoting healthier lifestyles. However, ensuring their reliability and user acceptance requires effective strategies for rebalancing bikes. This study introduces a novel approach to address the real-time rebalancing problem with a fleet of vehicles. It employs a dual policy reinforcement learning algorithm that decouples inventory and routing decisions, enhancing realism and efficiency compared to previous methods where both decisions were made simultaneously. We first formulate the inventory and routing subproblems as a multi-agent Markov Decision Process within a continuous time framework. Subsequently, we propose a DQN-based dual policy framework to jointly estimate the value functions, minimizing the lost demand. To facilitate learning, a comprehensive simulator is applied to operate under a first-arrive-first-serve rule, which enables the computation of immediate rewards across diverse demand scenarios. We conduct extensive experiments on various datasets generated from historical real-world data, affected by both temporal and weather factors. Our proposed algorithm demonstrates significant performance improvements over previous baseline methods. It offers valuable practical insights for operators and further explores the incorporation of reinforcement learning into real-world dynamic programming problems, paving the way for more intelligent and robust urban mobility solutions.
Actively Learning Combinatorial Optimization Using a Membership Oracle
May 23, 2024



Abstract:We consider solving a combinatorial optimization problem with an unknown linear constraint using a membership oracle that, given a solution, determines whether it is feasible or infeasible with absolute certainty. The goal of the decision maker is to find the best possible solution subject to a budget on the number of oracle calls. Inspired by active learning based on Support Vector Machines (SVMs), we adapt a classical framework in order to solve the problem by learning and exploiting a surrogate linear constraint. The resulting new framework includes training a linear separator on the labeled points and selecting new points to be labeled, which is achieved by applying a sampling strategy and solving a 0-1 integer linear program. Following the active learning literature, one can consider using SVM as a linear classifier and the information-based sampling strategy known as Simple margin. We improve on both sides: we propose an alternative sampling strategy based on mixed-integer quadratic programming and a linear separation method inspired by an algorithm for convex optimization in the oracle model. We conduct experiments on the pure knapsack problem and on a college study plan problem from the literature to show how different linear separation methods and sampling strategies influence the quality of the results in terms of objective value.
One-for-many Counterfactual Explanations by Column Generation
Feb 12, 2024



Abstract:In this paper, we consider the problem of generating a set of counterfactual explanations for a group of instances, with the one-for-many allocation rule, where one explanation is allocated to a subgroup of the instances. For the first time, we solve the problem of minimizing the number of explanations needed to explain all the instances, while considering sparsity by limiting the number of features allowed to be changed collectively in each explanation. A novel column generation framework is developed to efficiently search for the explanations. Our framework can be applied to any black-box classifier, like neural networks. Compared with a simple adaptation of a mixed-integer programming formulation from the literature, the column generation framework dominates in terms of scalability, computational performance and quality of the solutions.
Machine Learning Augmented Branch and Bound for Mixed Integer Linear Programming
Feb 08, 2024



Abstract:Mixed Integer Linear Programming (MILP) is a pillar of mathematical optimization that offers a powerful modeling language for a wide range of applications. During the past decades, enormous algorithmic progress has been made in solving MILPs, and many commercial and academic software packages exist. Nevertheless, the availability of data, both from problem instances and from solvers, and the desire to solve new problems and larger (real-life) instances, trigger the need for continuing algorithmic development. MILP solvers use branch and bound as their main component. In recent years, there has been an explosive development in the use of machine learning algorithms for enhancing all main tasks involved in the branch-and-bound algorithm, such as primal heuristics, branching, cutting planes, node selection and solver configuration decisions. This paper presents a survey of such approaches, addressing the vision of integration of machine learning and mathematical optimization as complementary technologies, and how this integration can benefit MILP solving. In particular, we give detailed attention to machine learning algorithms that automatically optimize some metric of branch-and-bound efficiency. We also address how to represent MILPs in the context of applying learning algorithms, MILP benchmarks and software.
A Reinforcement Learning Approach for Dynamic Rebalancing in Bike-Sharing System
Feb 05, 2024


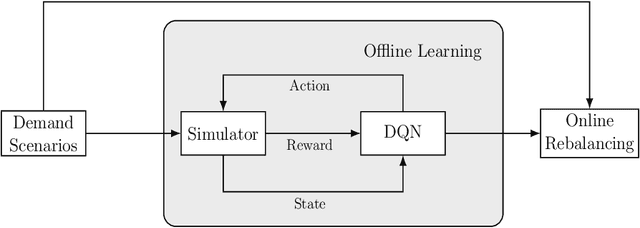
Abstract:Bike-Sharing Systems provide eco-friendly urban mobility, contributing to the alleviation of traffic congestion and to healthier lifestyles. Efficiently operating such systems and maintaining high customer satisfaction is challenging due to the stochastic nature of trip demand, leading to full or empty stations. Devising effective rebalancing strategies using vehicles to redistribute bikes among stations is therefore of uttermost importance for operators. As a promising alternative to classical mathematical optimization, reinforcement learning is gaining ground to solve sequential decision-making problems. This paper introduces a spatio-temporal reinforcement learning algorithm for the dynamic rebalancing problem with multiple vehicles. We first formulate the problem as a Multi-agent Markov Decision Process in a continuous time framework. This allows for independent and cooperative vehicle rebalancing, eliminating the impractical restriction of time-discretized models where vehicle departures are synchronized. A comprehensive simulator under the first-arrive-first-serve rule is then developed to facilitate the learning process by computing immediate rewards under diverse demand scenarios. To estimate the value function and learn the rebalancing policy, various Deep Q-Network configurations are tested, minimizing the lost demand. Experiments are carried out on various datasets generated from historical data, affected by both temporal and weather factors. The proposed algorithms outperform benchmarks, including a multi-period Mixed-Integer Programming model, in terms of lost demand. Once trained, it yields immediate decisions, making it suitable for real-time applications. Our work offers practical insights for operators and enriches the integration of reinforcement learning into dynamic rebalancing problems, paving the way for more intelligent and robust urban mobility solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge