Dual Policy Reinforcement Learning for Real-time Rebalancing in Bike-sharing Systems

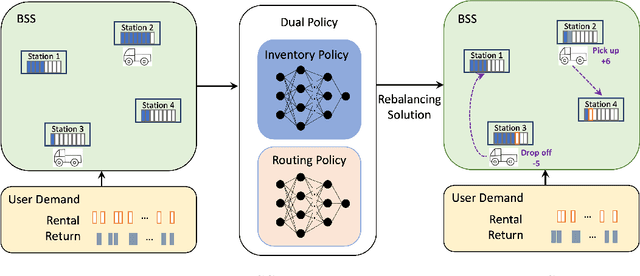
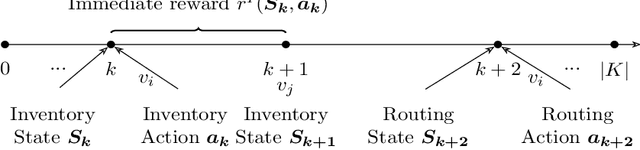
Bike-sharing systems play a crucial role in easing traffic congestion and promoting healthier lifestyles. However, ensuring their reliability and user acceptance requires effective strategies for rebalancing bikes. This study introduces a novel approach to address the real-time rebalancing problem with a fleet of vehicles. It employs a dual policy reinforcement learning algorithm that decouples inventory and routing decisions, enhancing realism and efficiency compared to previous methods where both decisions were made simultaneously. We first formulate the inventory and routing subproblems as a multi-agent Markov Decision Process within a continuous time framework. Subsequently, we propose a DQN-based dual policy framework to jointly estimate the value functions, minimizing the lost demand. To facilitate learning, a comprehensive simulator is applied to operate under a first-arrive-first-serve rule, which enables the computation of immediate rewards across diverse demand scenarios. We conduct extensive experiments on various datasets generated from historical real-world data, affected by both temporal and weather factors. Our proposed algorithm demonstrates significant performance improvements over previous baseline methods. It offers valuable practical insights for operators and further explores the incorporation of reinforcement learning into real-world dynamic programming problems, paving the way for more intelligent and robust urban mobility solutions.

A Reinforcement Learning Approach for Dynamic Rebalancing in Bike-Sharing System

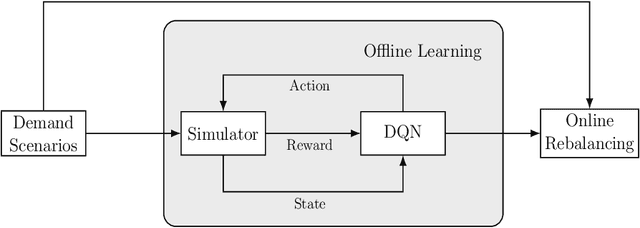
Bike-Sharing Systems provide eco-friendly urban mobility, contributing to the alleviation of traffic congestion and to healthier lifestyles. Efficiently operating such systems and maintaining high customer satisfaction is challenging due to the stochastic nature of trip demand, leading to full or empty stations. Devising effective rebalancing strategies using vehicles to redistribute bikes among stations is therefore of uttermost importance for operators. As a promising alternative to classical mathematical optimization, reinforcement learning is gaining ground to solve sequential decision-making problems. This paper introduces a spatio-temporal reinforcement learning algorithm for the dynamic rebalancing problem with multiple vehicles. We first formulate the problem as a Multi-agent Markov Decision Process in a continuous time framework. This allows for independent and cooperative vehicle rebalancing, eliminating the impractical restriction of time-discretized models where vehicle departures are synchronized. A comprehensive simulator under the first-arrive-first-serve rule is then developed to facilitate the learning process by computing immediate rewards under diverse demand scenarios. To estimate the value function and learn the rebalancing policy, various Deep Q-Network configurations are tested, minimizing the lost demand. Experiments are carried out on various datasets generated from historical data, affected by both temporal and weather factors. The proposed algorithms outperform benchmarks, including a multi-period Mixed-Integer Programming model, in terms of lost demand. Once trained, it yields immediate decisions, making it suitable for real-time applications. Our work offers practical insights for operators and enriches the integration of reinforcement learning into dynamic rebalancing problems, paving the way for more intelligent and robust urban mobility solutions.

A machine learning framework for neighbor generation in metaheuristic search

This paper presents a methodology for integrating machine learning techniques into metaheuristics for solving combinatorial optimization problems. Namely, we propose a general machine learning framework for neighbor generation in metaheuristic search. We first define an efficient neighborhood structure constructed by applying a transformation to a selected subset of variables from the current solution. Then, the key of the proposed methodology is to generate promising neighbors by selecting a proper subset of variables that contains a descent of the objective in the solution space. To learn a good variable selection strategy, we formulate the problem as a classification task that exploits structural information from the characteristics of the problem and from high-quality solutions. We validate our methodology on two metaheuristic applications: a Tabu Search scheme for solving a Wireless Network Optimization problem and a Large Neighborhood Search heuristic for solving Mixed-Integer Programs. The experimental results show that our approach is able to achieve a satisfactory trade-off between the exploration of a larger solution space and the exploitation of high-quality solution regions on both applications.

Design and Implementation of an Heuristic-Enhanced Branch-and-Bound Solver for MILP

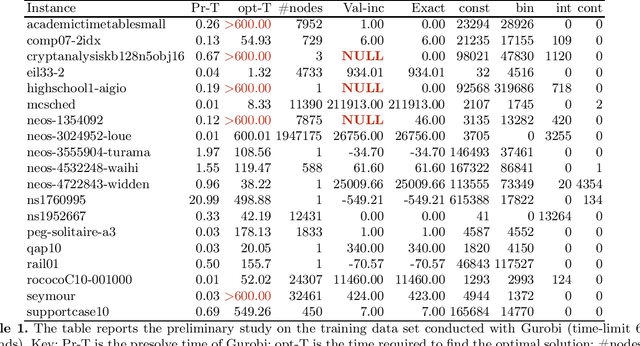
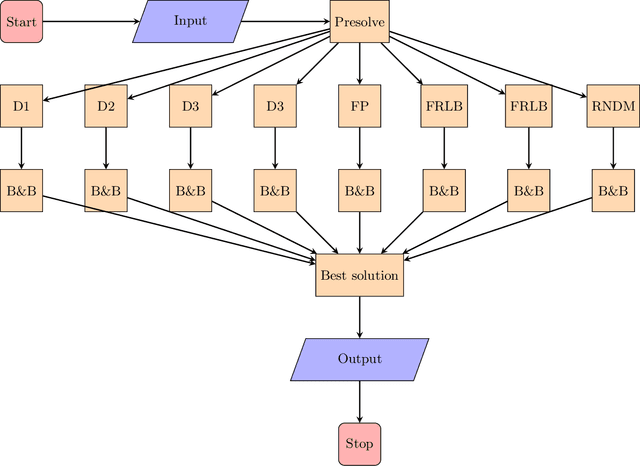
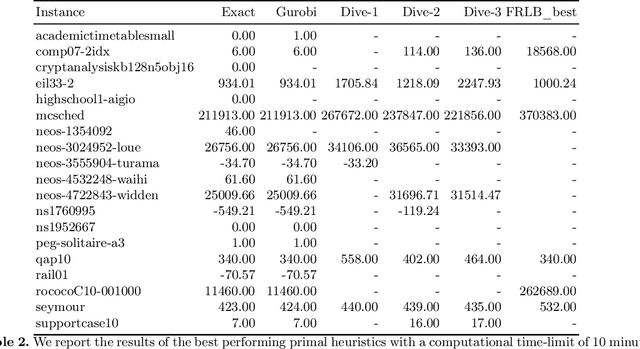
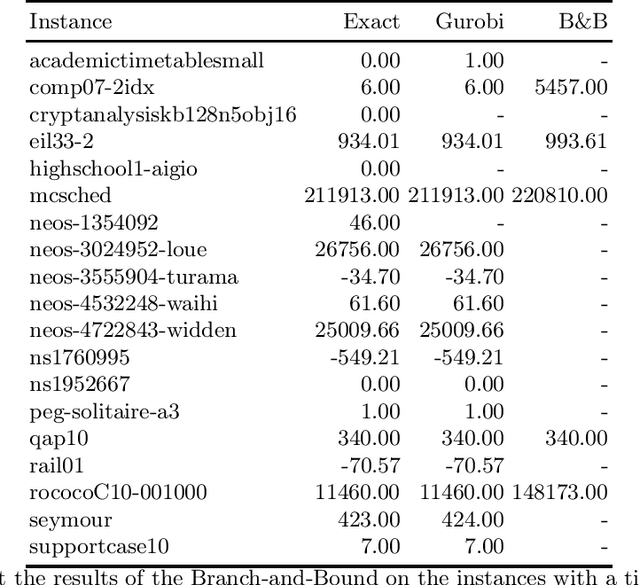
We present a solver for Mixed Integer Programs (MIP) developed for the MIP competition 2022. Given the 10 minutes bound on the computational time established by the rules of the competition, our method focuses on finding a feasible solution and improves it through a Branch-and-Bound algorithm. Another rule of the competition allows the use of up to 8 threads. Each thread is given a different primal heuristic, which has been tuned by hyper-parameters, to find a feasible solution. In every thread, once a feasible solution is found, we stop and we use a Branch-and-Bound method, embedded with local search heuristics, to ameliorate the incumbent solution. The three variants of the Diving heuristic that we implemented manage to find a feasible solution for 10 instances of the training data set. These heuristics are the best performing among the heuristics that we implemented. Our Branch-and-Bound algorithm is effective on a small portion of the training data set, and it manages to find an incumbent feasible solution for an instance that we could not solve with the Diving heuristics. Overall, our combined methods, when implemented with extensive computational power, can solve 11 of the 19 problems of the training data set within the time limit. Our submission to the MIP competition was awarded the "Outstanding Student Submission" honorable mention.

Learning to Search in Local Branching

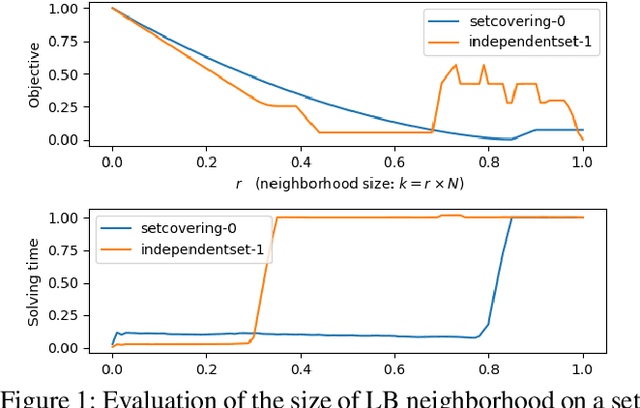
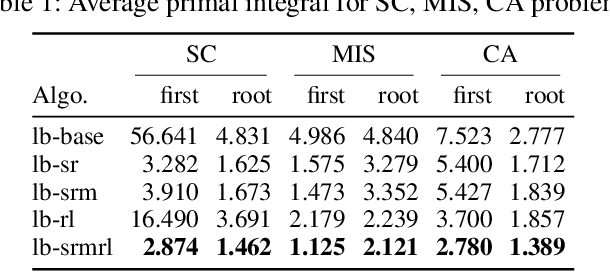
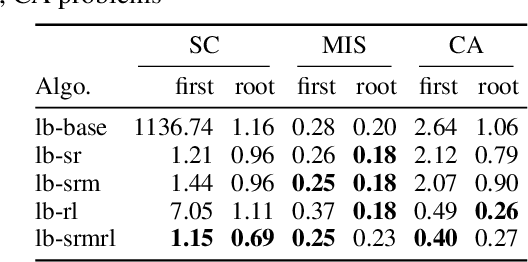
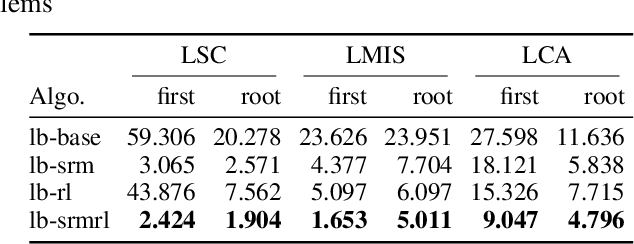
Finding high-quality solutions to mixed-integer linear programming problems (MILPs) is of great importance for many practical applications. In this respect, the refinement heuristic local branching (LB) has been proposed to produce improving solutions and has been highly influential for the development of local search methods in MILP. The algorithm iteratively explores a sequence of solution neighborhoods defined by the so-called local branching constraint, namely, a linear inequality limiting the distance from a reference solution. For a LB algorithm, the choice of the neighborhood size is critical to performance. Although it was initialized by a conservative value in the original LB scheme, our new observation is that the best size is strongly dependent on the particular MILP instance. In this work, we investigate the relation between the size of the search neighborhood and the behavior of the underlying LB algorithm, and we devise a leaning based framework for guiding the neighborhood search of the LB heuristic. The framework consists of a two-phase strategy. For the first phase, a scaled regression model is trained to predict the size of the LB neighborhood at the first iteration through a regression task. In the second phase, we leverage reinforcement learning and devise a reinforced neighborhood search strategy to dynamically adapt the size at the subsequent iterations. We computationally show that the neighborhood size can indeed be learned, leading to improved performances and that the overall algorithm generalizes well both with respect to the instance size and, remarkably, across instances.

Learning chordal extensions

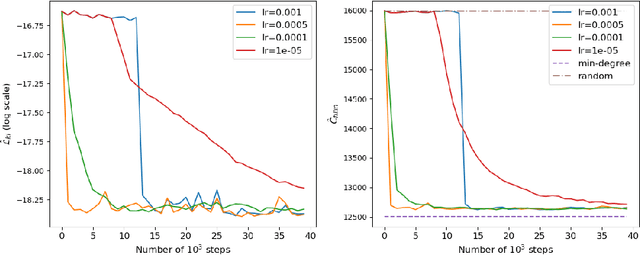
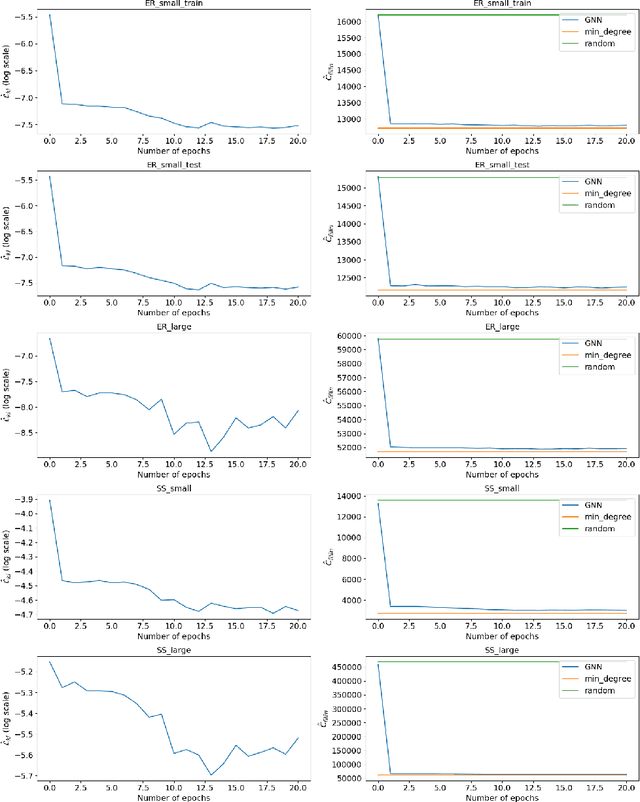
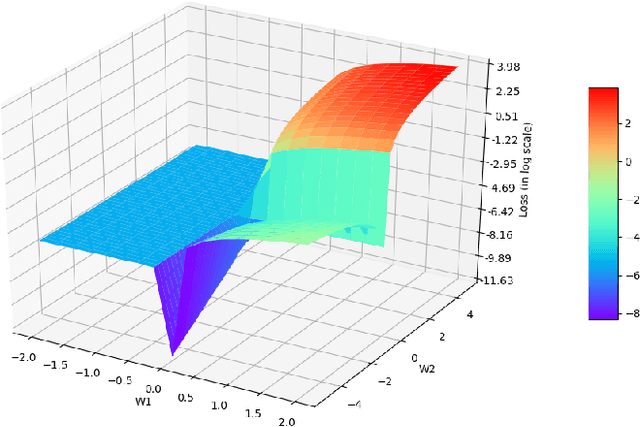
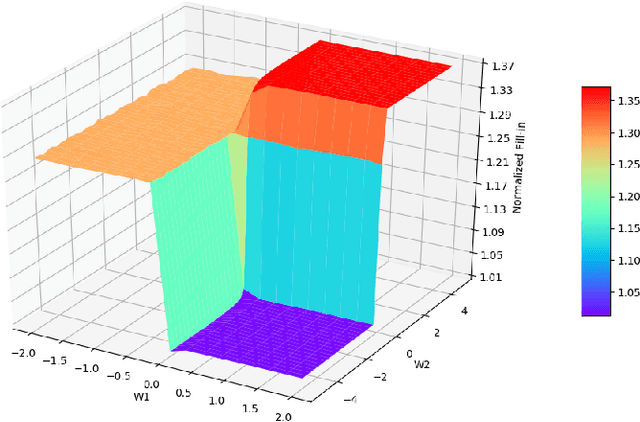
A highly influential ingredient of many techniques designed to exploit sparsity in numerical optimization is the so-called chordal extension of a graph representation of the optimization problem. The definitive relation between chordal extension and the performance of the optimization algorithm that uses the extension is not a mathematically understood task. For this reason, we follow the current research trend of looking at Combinatorial Optimization tasks by using a Machine Learning lens, and we devise a framework for learning elimination rules yielding high-quality chordal extensions. As a first building block of the learning framework, we propose an on-policy imitation learning scheme that mimics the elimination ordering provided by the (classical) minimum degree rule. The results show that our on-policy imitation learning approach is effective in learning the minimum degree policy and, consequently, produces graphs with desirable fill-in characteristics.