Learning to Search in Local Branching

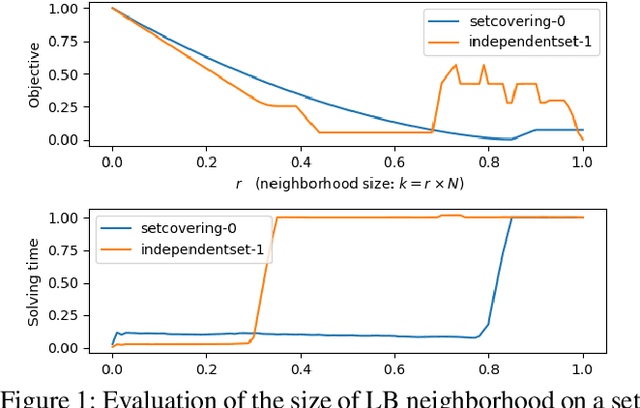
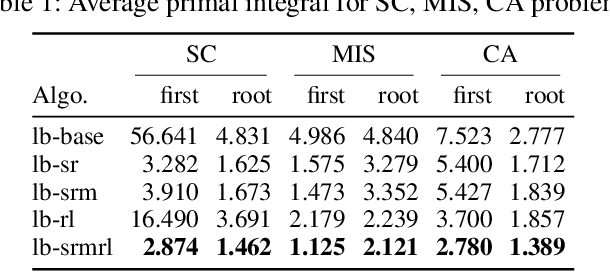
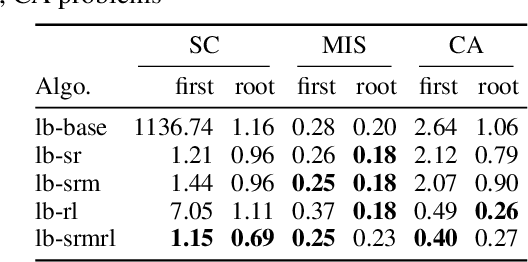
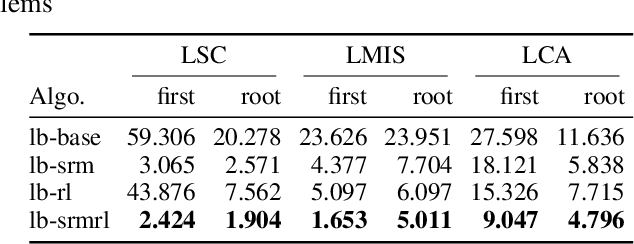
Finding high-quality solutions to mixed-integer linear programming problems (MILPs) is of great importance for many practical applications. In this respect, the refinement heuristic local branching (LB) has been proposed to produce improving solutions and has been highly influential for the development of local search methods in MILP. The algorithm iteratively explores a sequence of solution neighborhoods defined by the so-called local branching constraint, namely, a linear inequality limiting the distance from a reference solution. For a LB algorithm, the choice of the neighborhood size is critical to performance. Although it was initialized by a conservative value in the original LB scheme, our new observation is that the best size is strongly dependent on the particular MILP instance. In this work, we investigate the relation between the size of the search neighborhood and the behavior of the underlying LB algorithm, and we devise a leaning based framework for guiding the neighborhood search of the LB heuristic. The framework consists of a two-phase strategy. For the first phase, a scaled regression model is trained to predict the size of the LB neighborhood at the first iteration through a regression task. In the second phase, we leverage reinforcement learning and devise a reinforced neighborhood search strategy to dynamically adapt the size at the subsequent iterations. We computationally show that the neighborhood size can indeed be learned, leading to improved performances and that the overall algorithm generalizes well both with respect to the instance size and, remarkably, across instances.

Embedded hyper-parameter tuning by Simulated Annealing

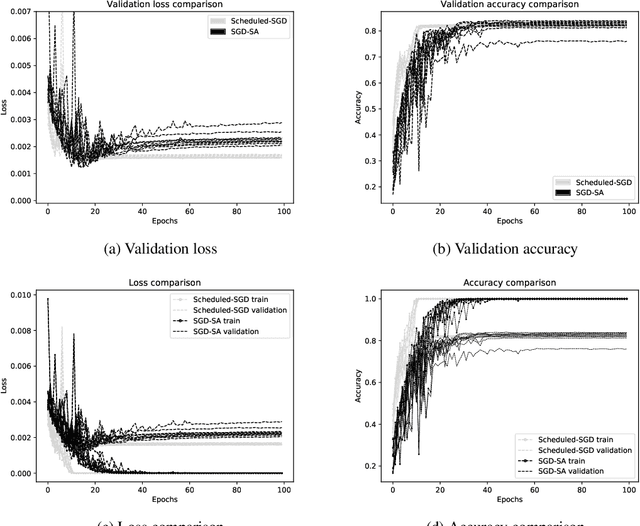
We propose a new metaheuristic training scheme that combines Stochastic Gradient Descent (SGD) and Discrete Optimization in an unconventional way. Our idea is to define a discrete neighborhood of the current SGD point containing a number of "potentially good moves" that exploit gradient information, and to search this neighborhood by using a classical metaheuristic scheme borrowed from Discrete Optimization. In the present paper we investigate the use of a simple Simulated Annealing (SA) metaheuristic that accepts/rejects a candidate new solution in the neighborhood with a probability that depends both on the new solution quality and on a parameter (the temperature) which is modified over time to lower the probability of accepting worsening moves. We use this scheme as an automatic way to perform hyper-parameter tuning, hence the title of the paper. A distinctive feature of our scheme is that hyper-parameters are modified within a single SGD execution (and not in an external loop, as customary) and evaluated on the fly on the current minibatch, i.e., their tuning is fully embedded within the SGD algorithm. The use of SA for training is not new, but previous proposals were mainly intended for non-differentiable objective functions for which SGD is not applied due to the lack of gradients. On the contrary, our SA method requires differentiability of (a proxy of) the loss function, and leverages on the availability of a gradient direction to define local moves that have a large probability to improve the current solution. Computational results on image classification (CIFAR-10) are reported, showing that the proposed approach leads to an improvement of the final validation accuracy for modern Deep Neural Networks such as ResNet34 and VGG16.

Faster SGD training by minibatch persistency

It is well known that, for most datasets, the use of large-size minibatches for Stochastic Gradient Descent (SGD) typically leads to slow convergence and poor generalization. On the other hand, large minibatches are of great practical interest as they allow for a better exploitation of modern GPUs. Previous literature on the subject concentrated on how to adjust the main SGD parameters (in particular, the learning rate) when using large minibatches. In this work we introduce an additional feature, that we call minibatch persistency, that consists in reusing the same minibatch for K consecutive SGD iterations. The computational conjecture here is that a large minibatch contains a significant sample of the training set, so one can afford to slightly overfitting it without worsening generalization too much. The approach is intended to speedup SGD convergence, and also has the advantage of reducing the overhead related to data loading on the internal GPU memory. We present computational results on CIFAR-10 with an AlexNet architecture, showing that even small persistency values (K=2 or 5) already lead to a significantly faster convergence and to a comparable (or even better) generalization than the standard "disposable minibatch" approach (K=1), in particular when large minibatches are used. The lesson learned is that minibatch persistency can be a simple yet effective way to deal with large minibatches.

Deep Neural Networks as 0-1 Mixed Integer Linear Programs: A Feasibility Study

Deep Neural Networks (DNNs) are very popular these days, and are the subject of a very intense investigation. A DNN is made by layers of internal units (or neurons), each of which computes an affine combination of the output of the units in the previous layer, applies a nonlinear operator, and outputs the corresponding value (also known as activation). A commonly-used nonlinear operator is the so-called rectified linear unit (ReLU), whose output is just the maximum between its input value and zero. In this (and other similar cases like max pooling, where the max operation involves more than one input value), one can model the DNN as a 0-1 Mixed Integer Linear Program (0-1 MILP) where the continuous variables correspond to the output values of each unit, and a binary variable is associated with each ReLU to model its yes/no nature. In this paper we discuss the peculiarity of this kind of 0-1 MILP models, and describe an effective bound-tightening technique intended to ease its solution. We also present possible applications of the 0-1 MILP model arising in feature visualization and in the construction of adversarial examples. Preliminary computational results are reported, aimed at investigating (on small DNNs) the computational performance of a state-of-the-art MILP solver when applied to a known test case, namely, hand-written digit recognition.