Learning chordal extensions
Paper and Code
Oct 16, 2019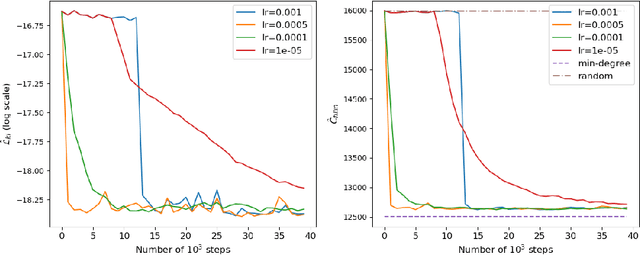
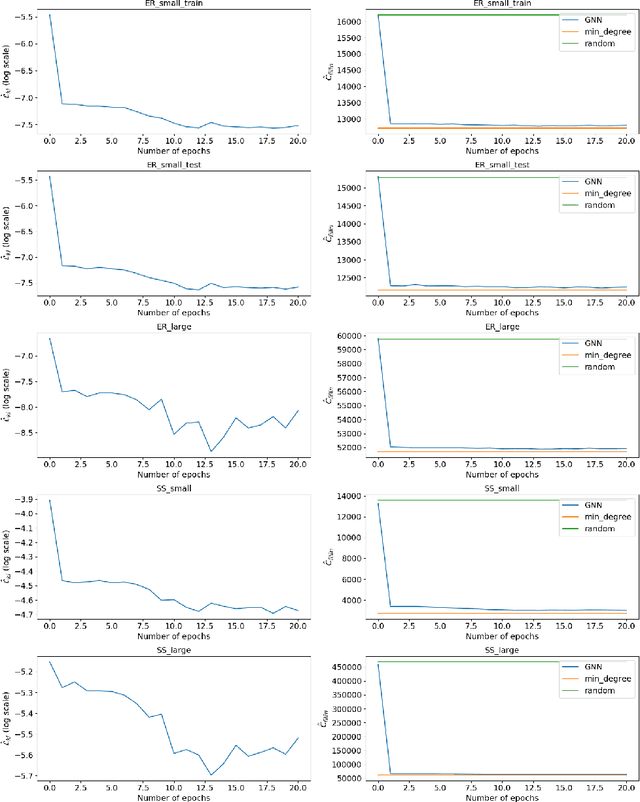
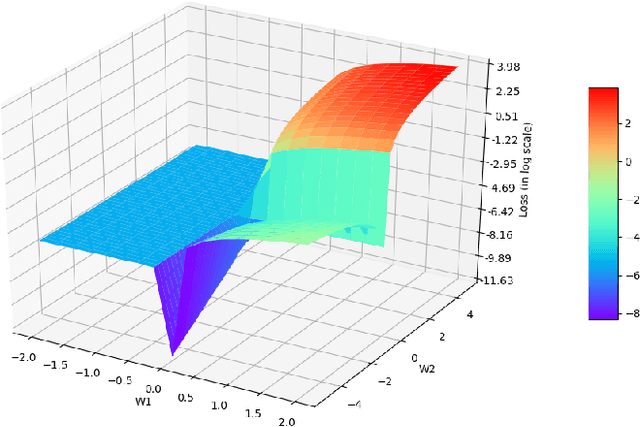
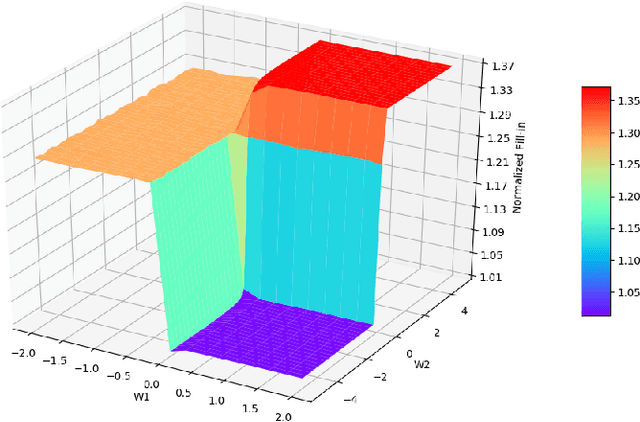
A highly influential ingredient of many techniques designed to exploit sparsity in numerical optimization is the so-called chordal extension of a graph representation of the optimization problem. The definitive relation between chordal extension and the performance of the optimization algorithm that uses the extension is not a mathematically understood task. For this reason, we follow the current research trend of looking at Combinatorial Optimization tasks by using a Machine Learning lens, and we devise a framework for learning elimination rules yielding high-quality chordal extensions. As a first building block of the learning framework, we propose an on-policy imitation learning scheme that mimics the elimination ordering provided by the (classical) minimum degree rule. The results show that our on-policy imitation learning approach is effective in learning the minimum degree policy and, consequently, produces graphs with desirable fill-in characteristics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge