Design and Implementation of an Heuristic-Enhanced Branch-and-Bound Solver for MILP

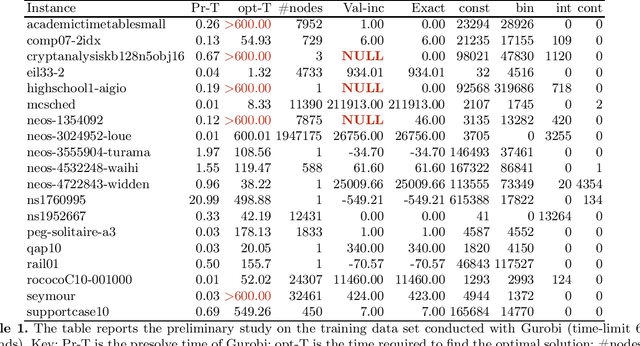
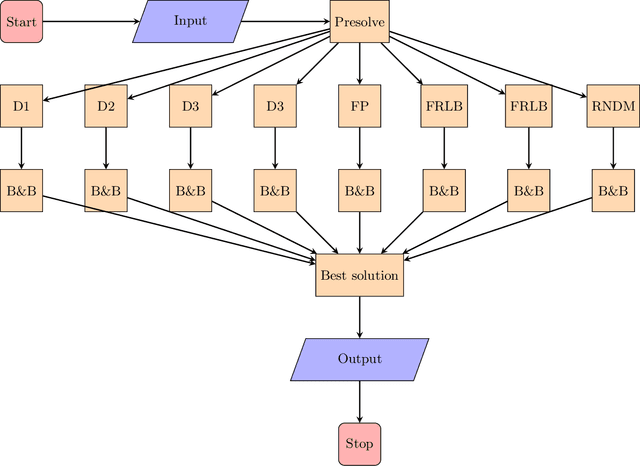
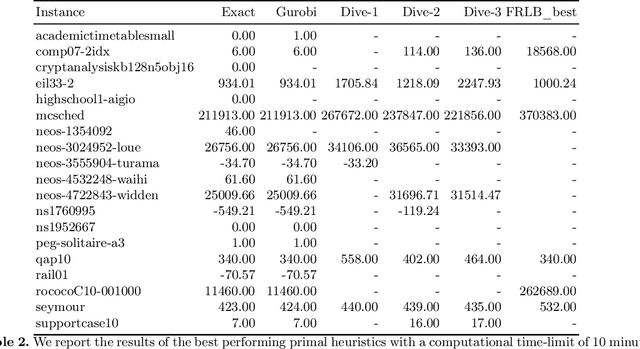
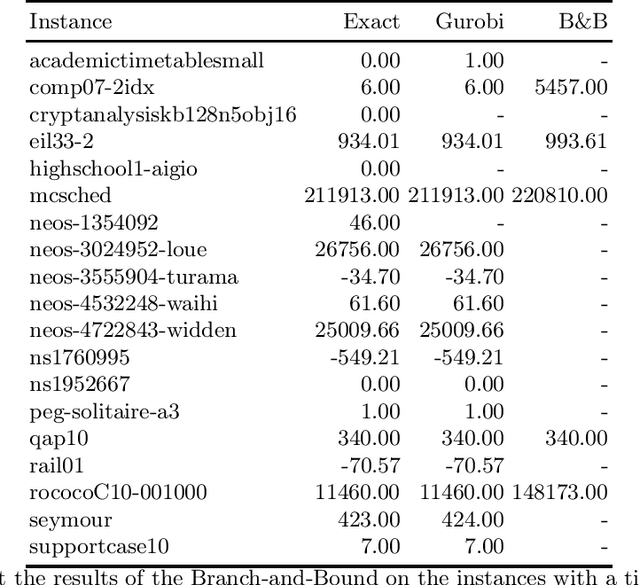
We present a solver for Mixed Integer Programs (MIP) developed for the MIP competition 2022. Given the 10 minutes bound on the computational time established by the rules of the competition, our method focuses on finding a feasible solution and improves it through a Branch-and-Bound algorithm. Another rule of the competition allows the use of up to 8 threads. Each thread is given a different primal heuristic, which has been tuned by hyper-parameters, to find a feasible solution. In every thread, once a feasible solution is found, we stop and we use a Branch-and-Bound method, embedded with local search heuristics, to ameliorate the incumbent solution. The three variants of the Diving heuristic that we implemented manage to find a feasible solution for 10 instances of the training data set. These heuristics are the best performing among the heuristics that we implemented. Our Branch-and-Bound algorithm is effective on a small portion of the training data set, and it manages to find an incumbent feasible solution for an instance that we could not solve with the Diving heuristics. Overall, our combined methods, when implemented with extensive computational power, can solve 11 of the 19 problems of the training data set within the time limit. Our submission to the MIP competition was awarded the "Outstanding Student Submission" honorable mention.

The First AI4TSP Competition: Learning to Solve Stochastic Routing Problems

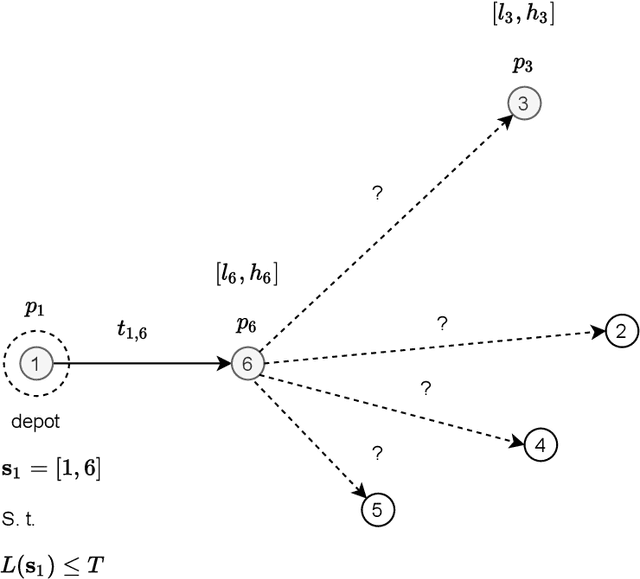
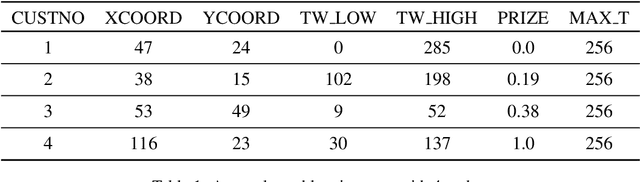
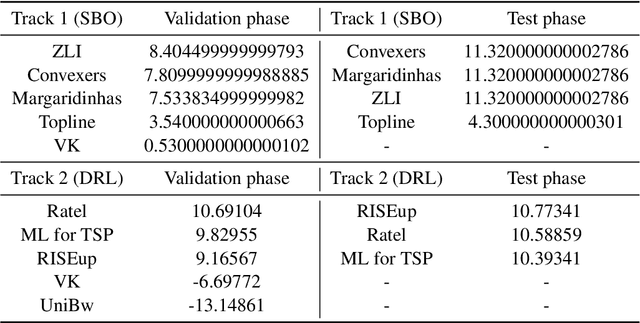
This paper reports on the first international competition on AI for the traveling salesman problem (TSP) at the International Joint Conference on Artificial Intelligence 2021 (IJCAI-21). The TSP is one of the classical combinatorial optimization problems, with many variants inspired by real-world applications. This first competition asked the participants to develop algorithms to solve a time-dependent orienteering problem with stochastic weights and time windows (TD-OPSWTW). It focused on two types of learning approaches: surrogate-based optimization and deep reinforcement learning. In this paper, we describe the problem, the setup of the competition, the winning methods, and give an overview of the results. The winning methods described in this work have advanced the state-of-the-art in using AI for stochastic routing problems. Overall, by organizing this competition we have introduced routing problems as an interesting problem setting for AI researchers. The simulator of the problem has been made open-source and can be used by other researchers as a benchmark for new AI methods.