Revisit the Algorithm Selection Problem for TSP with Spatial Information Enhanced Graph Neural Networks

Algorithm selection is a well-known problem where researchers investigate how to construct useful features representing the problem instances and then apply feature-based machine learning models to predict which algorithm works best with the given instance. However, even for simple optimization problems such as Euclidean Traveling Salesman Problem (TSP), there lacks a general and effective feature representation for problem instances. The important features of TSP are relatively well understood in the literature, based on extensive domain knowledge and post-analysis of the solutions. In recent years, Convolutional Neural Network (CNN) has become a popular approach to select algorithms for TSP. Compared to traditional feature-based machine learning models, CNN has an automatic feature-learning ability and demands less domain expertise. However, it is still required to generate intermediate representations, i.e., multiple images to represent TSP instances first. In this paper, we revisit the algorithm selection problem for TSP, and propose a novel Graph Neural Network (GNN), called GINES. GINES takes the coordinates of cities and distances between cities as input. It is composed of a new message-passing mechanism and a local neighborhood feature extractor to learn spatial information of TSP instances. We evaluate GINES on two benchmark datasets. The results show that GINES outperforms CNN and the original GINE models. It is better than the traditional handcrafted feature-based approach on one dataset. The code and dataset will be released in the final version of this paper.

Digital Twin Applications in Urban Logistics: An Overview

Urban traffic attributed to commercial and industrial transportation is observed to largely affect living standards in cities due to external effects pertaining to pollution and congestion. In order to counter this, smart cities deploy technological tools to achieve sustainability. Such tools include Digital Twins (DT)s which are virtual replicas of real-life physical systems. Research suggests that DTs can be very beneficial in how they control a physical system by constantly optimizing its performance. The concept has been extensively studied in other technology-driven industries like manufacturing. However, little work has been done with regards to their application in urban logistics. In this paper, we seek to provide a framework by which DTs could be easily adapted to urban logistics networks. To do this, we provide a characterization of key factors in urban logistics for dynamic decision-making. We also survey previous research on DT applications in urban logistics as we found that a holistic overview is lacking. Using this knowledge in combination with the characterization, we produce a conceptual model that describes the ontology, learning capabilities and optimization prowess of an urban logistics digital twin through its quantitative models. We finish off with a discussion on potential research benefits and limitations based on previous research and our practical experience.

Learning Adaptive Evolutionary Computation for Solving Multi-Objective Optimization Problems

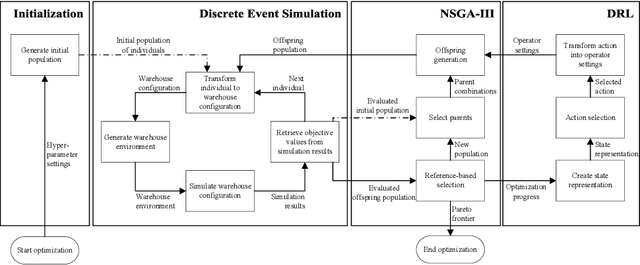
Multi-objective evolutionary algorithms (MOEAs) are widely used to solve multi-objective optimization problems. The algorithms rely on setting appropriate parameters to find good solutions. However, this parameter tuning could be very computationally expensive in solving non-trial (combinatorial) optimization problems. This paper proposes a framework that integrates MOEAs with adaptive parameter control using Deep Reinforcement Learning (DRL). The DRL policy is trained to adaptively set the values that dictate the intensity and probability of mutation for solutions during optimization. We test the proposed approach with a simple benchmark problem and a real-world, complex warehouse design and control problem. The experimental results demonstrate the advantages of our method in terms of solution quality and computation time to reach good solutions. In addition, we show the learned policy is transferable, i.e., the policy trained on a simple benchmark problem can be directly applied to solve the complex warehouse optimization problem, effectively, without the need for retraining.

Machine Learning for Combinatorial Optimisation of Partially-Specified Problems: Regret Minimisation as a Unifying Lens

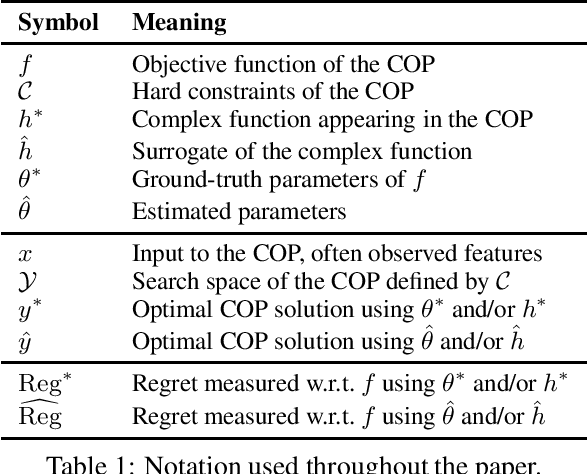
It is increasingly common to solve combinatorial optimisation problems that are partially-specified. We survey the case where the objective function or the relations between variables are not known or are only partially specified. The challenge is to learn them from available data, while taking into account a set of hard constraints that a solution must satisfy, and that solving the optimisation problem (esp. during learning) is computationally very demanding. This paper overviews four seemingly unrelated approaches, that can each be viewed as learning the objective function of a hard combinatorial optimisation problem: 1) surrogate-based optimisation, 2) empirical model learning, 3) decision-focused learning (`predict + optimise'), and 4) structured-output prediction. We formalise each learning paradigm, at first in the ways commonly found in the literature, and then bring the formalisations together in a compatible way using regret. We discuss the differences and interactions between these frameworks, highlight the opportunities for cross-fertilization and survey open directions.

The First AI4TSP Competition: Learning to Solve Stochastic Routing Problems

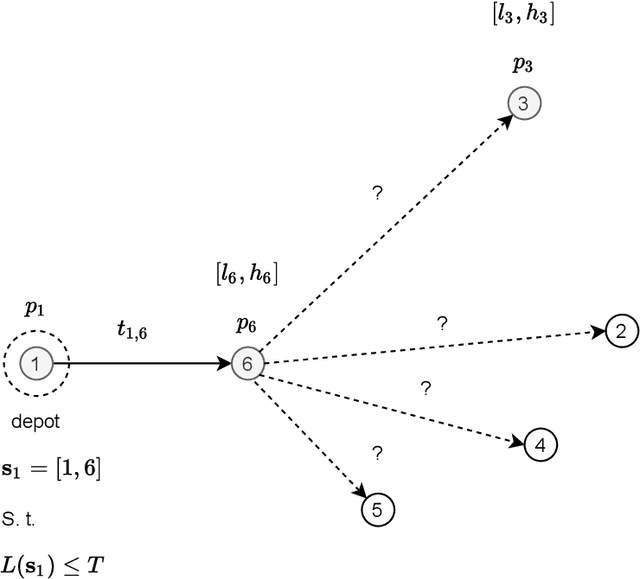
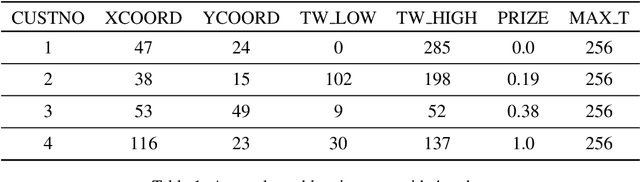
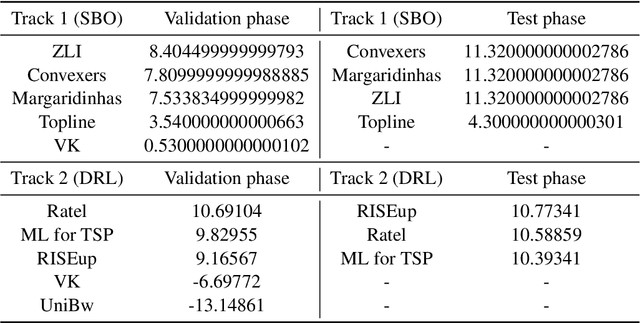
This paper reports on the first international competition on AI for the traveling salesman problem (TSP) at the International Joint Conference on Artificial Intelligence 2021 (IJCAI-21). The TSP is one of the classical combinatorial optimization problems, with many variants inspired by real-world applications. This first competition asked the participants to develop algorithms to solve a time-dependent orienteering problem with stochastic weights and time windows (TD-OPSWTW). It focused on two types of learning approaches: surrogate-based optimization and deep reinforcement learning. In this paper, we describe the problem, the setup of the competition, the winning methods, and give an overview of the results. The winning methods described in this work have advanced the state-of-the-art in using AI for stochastic routing problems. Overall, by organizing this competition we have introduced routing problems as an interesting problem setting for AI researchers. The simulator of the problem has been made open-source and can be used by other researchers as a benchmark for new AI methods.

EXPObench: Benchmarking Surrogate-based Optimisation Algorithms on Expensive Black-box Functions

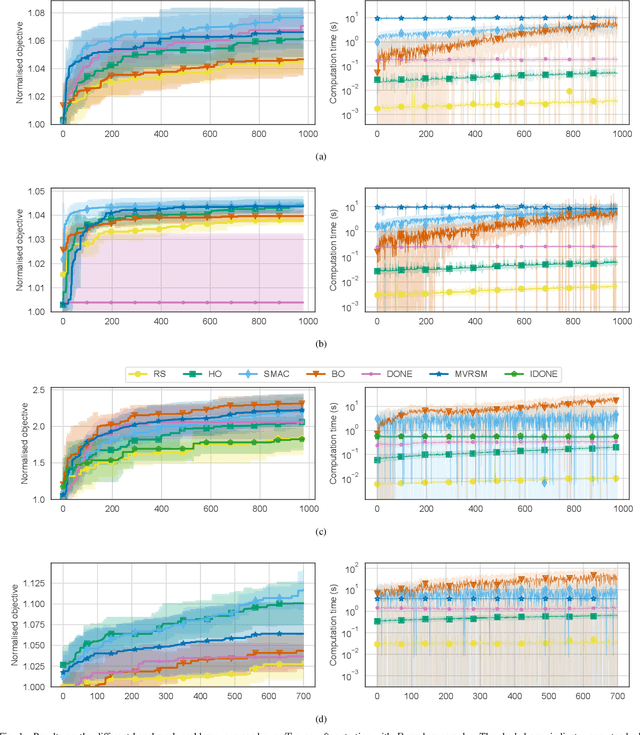
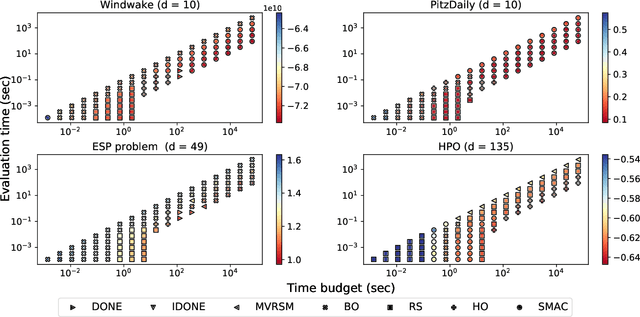
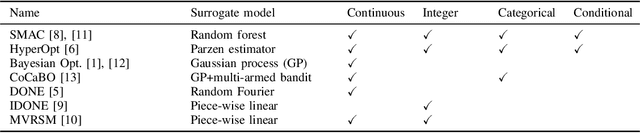
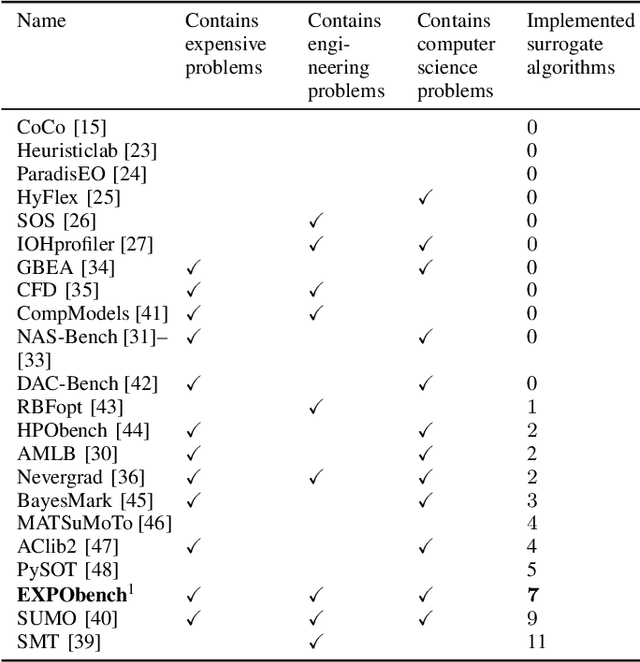
Surrogate algorithms such as Bayesian optimisation are especially designed for black-box optimisation problems with expensive objectives, such as hyperparameter tuning or simulation-based optimisation. In the literature, these algorithms are usually evaluated with synthetic benchmarks which are well established but have no expensive objective, and only on one or two real-life applications which vary wildly between papers. There is a clear lack of standardisation when it comes to benchmarking surrogate algorithms on real-life, expensive, black-box objective functions. This makes it very difficult to draw conclusions on the effect of algorithmic contributions. A new benchmark library, EXPObench, provides first steps towards such a standardisation. The library is used to provide an extensive comparison of six different surrogate algorithms on four expensive optimisation problems from different real-life applications. This has led to new insights regarding the relative importance of exploration, the evaluation time of the objective, and the used model. A further contribution is that we make the algorithms and benchmark problem instances publicly available, contributing to more uniform analysis of surrogate algorithms. Most importantly, we include the performance of the six algorithms on all evaluated problem instances. This results in a unique new dataset that lowers the bar for researching new methods as the number of expensive evaluations required for comparison is significantly reduced.

Continuous surrogate-based optimization algorithms are well-suited for expensive discrete problems

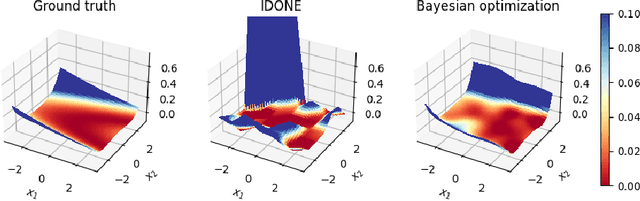
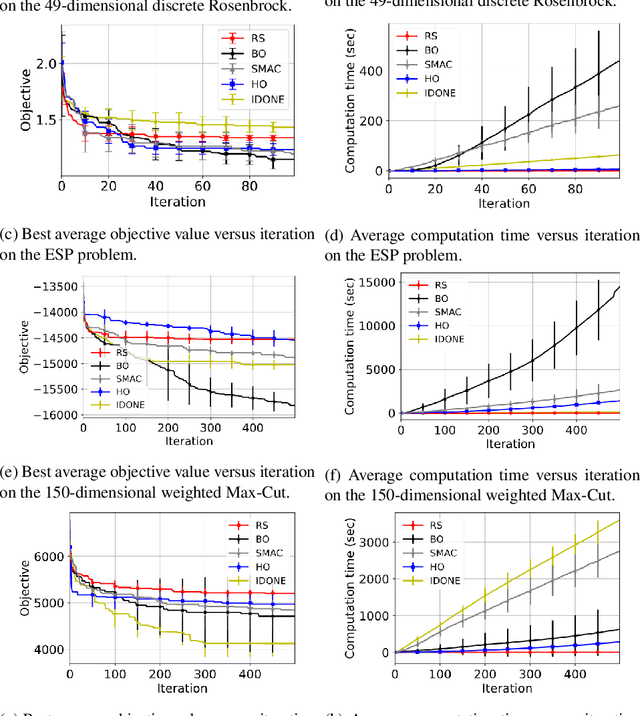
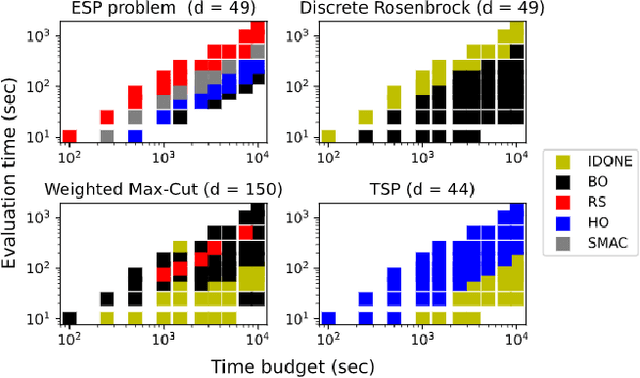
One method to solve expensive black-box optimization problems is to use a surrogate model that approximates the objective based on previous observed evaluations. The surrogate, which is cheaper to evaluate, is optimized instead to find an approximate solution to the original problem. In the case of discrete problems, recent research has revolved around surrogate models that are specifically constructed to deal with discrete structures. A main motivation is that literature considers continuous methods, such as Bayesian optimization with Gaussian processes as the surrogate, to be sub-optimal (especially in higher dimensions) because they ignore the discrete structure by e.g. rounding off real-valued solutions to integers. However, we claim that this is not true. In fact, we present empirical evidence showing that the use of continuous surrogate models displays competitive performance on a set of high-dimensional discrete benchmark problems, including a real-life application, against state-of-the-art discrete surrogate-based methods. Our experiments on different discrete structures and time constraints also give more insight into which algorithms work well on which type of problem.

Black-box Mixed-Variable Optimisation using a Surrogate Model that Satisfies Integer Constraints

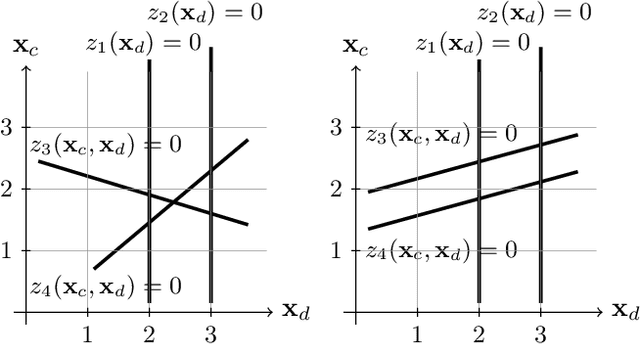
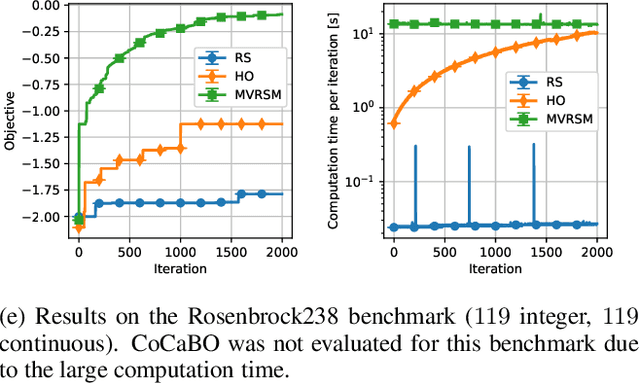
A challenging problem in both engineering and computer science is that of minimising a function for which we have no mathematical formulation available, that is expensive to evaluate, and that contains continuous and integer variables, for example in automatic algorithm configuration. Surrogate modelling techniques are very suitable for this type of problem, but most existing techniques are designed with only continuous or only discrete variables in mind. Mixed-Variable ReLU-based Surrogate Modelling (MVRSM) is a surrogate modelling algorithm that uses a linear combination of rectified linear units, defined in such a way that (local) optima satisfy the integer constraints. This method is both more accurate and more efficient than the state of the art on several benchmarks with up to 238 continuous and integer variables.

Black-box Combinatorial Optimization using Models with Integer-valued Minima

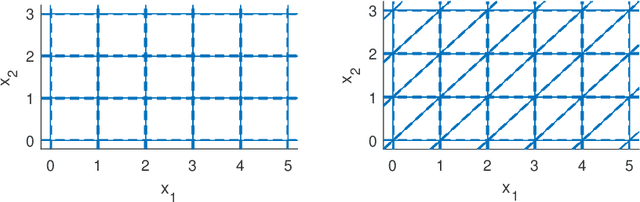
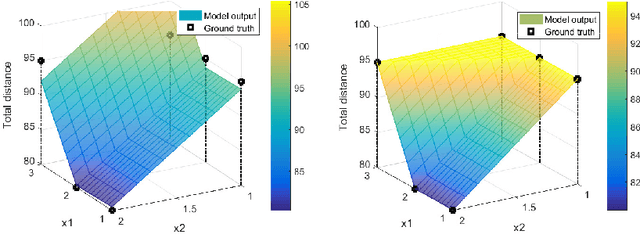
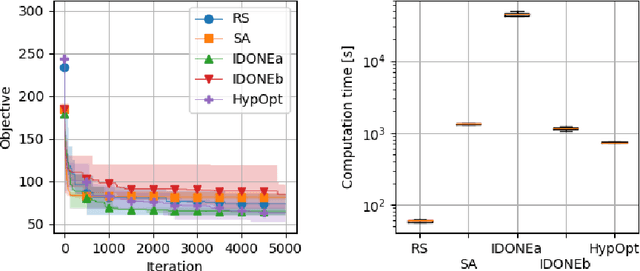
When a black-box optimization objective can only be evaluated with costly or noisy measurements, most standard optimization algorithms are unsuited to find the optimal solution. Specialized algorithms that deal with exactly this situation make use of surrogate models. These models are usually continuous and smooth, which is beneficial for continuous optimization problems, but not necessarily for combinatorial problems. However, by choosing the basis functions of the surrogate model in a certain way, we show that it can be guaranteed that the optimal solution of the surrogate model is integer. This approach outperforms random search, simulated annealing and one Bayesian optimization algorithm on the problem of finding robust routes for a noise-perturbed traveling salesman benchmark problem, with similar performance as another Bayesian optimization algorithm, and outperforms all compared algorithms on a convex binary optimization problem with a large number of variables.

Online Optimization with Costly and Noisy Measurements using Random Fourier Expansions

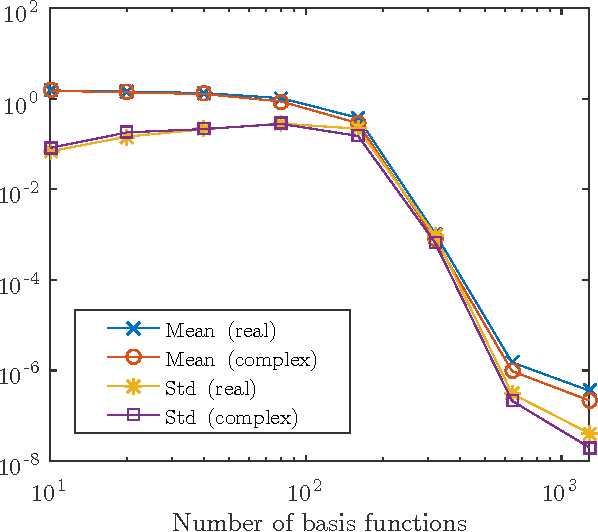
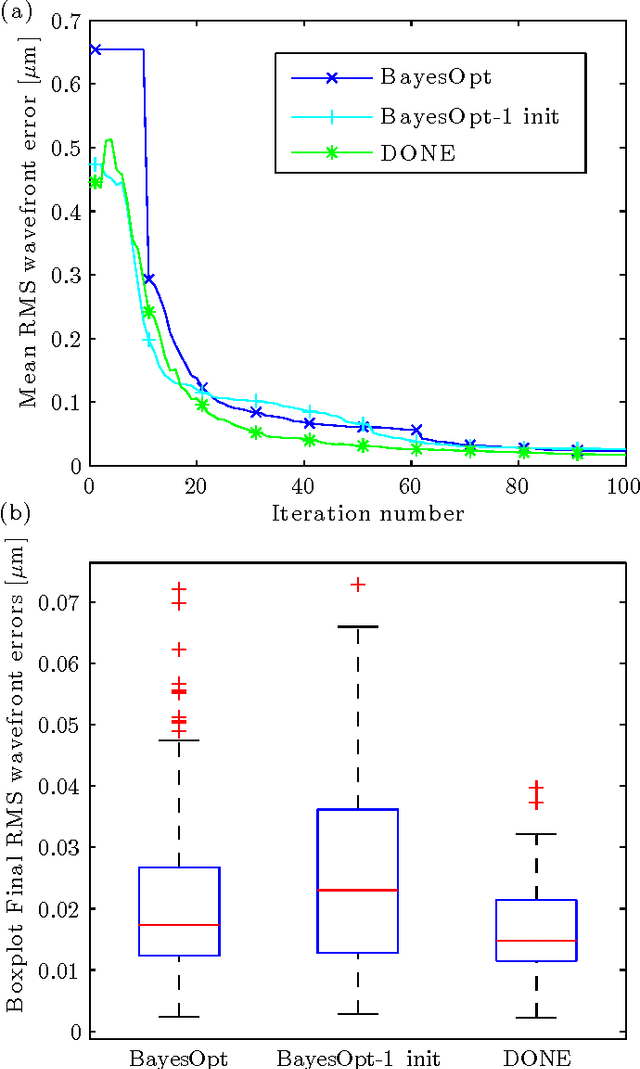
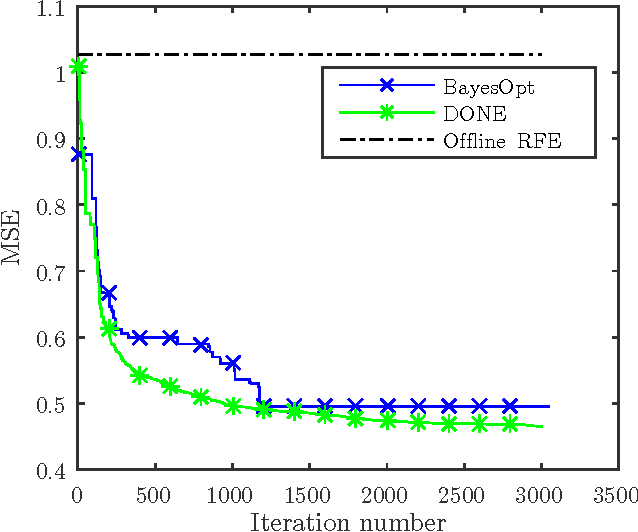
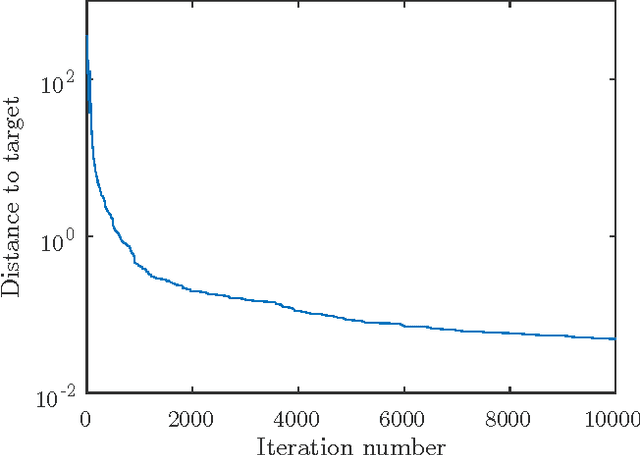
This paper analyzes DONE, an online optimization algorithm that iteratively minimizes an unknown function based on costly and noisy measurements. The algorithm maintains a surrogate of the unknown function in the form of a random Fourier expansion (RFE). The surrogate is updated whenever a new measurement is available, and then used to determine the next measurement point. The algorithm is comparable to Bayesian optimization algorithms, but its computational complexity per iteration does not depend on the number of measurements. We derive several theoretical results that provide insight on how the hyper-parameters of the algorithm should be chosen. The algorithm is compared to a Bayesian optimization algorithm for a benchmark problem and three applications, namely, optical coherence tomography, optical beam-forming network tuning, and robot arm control. It is found that the DONE algorithm is significantly faster than Bayesian optimization in the discussed problems, while achieving a similar or better performance.