Machine Learning for Combinatorial Optimisation of Partially-Specified Problems: Regret Minimisation as a Unifying Lens
Paper and Code
May 20, 2022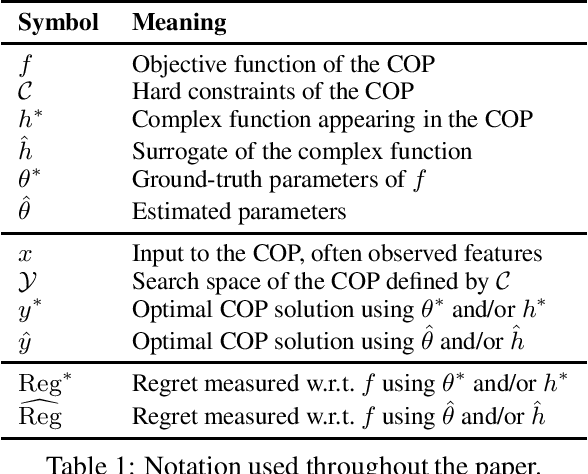

It is increasingly common to solve combinatorial optimisation problems that are partially-specified. We survey the case where the objective function or the relations between variables are not known or are only partially specified. The challenge is to learn them from available data, while taking into account a set of hard constraints that a solution must satisfy, and that solving the optimisation problem (esp. during learning) is computationally very demanding. This paper overviews four seemingly unrelated approaches, that can each be viewed as learning the objective function of a hard combinatorial optimisation problem: 1) surrogate-based optimisation, 2) empirical model learning, 3) decision-focused learning (`predict + optimise'), and 4) structured-output prediction. We formalise each learning paradigm, at first in the ways commonly found in the literature, and then bring the formalisations together in a compatible way using regret. We discuss the differences and interactions between these frameworks, highlight the opportunities for cross-fertilization and survey open directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge