Job Shop Scheduling Benchmark: Environments and Instances for Learning and Non-learning Methods

We introduce an open-source GitHub repository containing comprehensive benchmarks for a wide range of machine scheduling problems, including Job Shop Scheduling (JSP), Flow Shop Scheduling (FSP), Flexible Job Shop Scheduling (FJSP), FJSP with Assembly constraints (FAJSP), FJSP with Sequence-Dependent Setup Times (FJSP-SDST), and the online FJSP (with online job arrivals). Our primary goal is to provide a centralized hub for researchers, practitioners, and enthusiasts interested in tackling machine scheduling challenges.

Operator Selection in Adaptive Large Neighborhood Search using Deep Reinforcement Learning

Large Neighborhood Search (LNS) is a popular heuristic for solving combinatorial optimization problems. LNS iteratively explores the neighborhoods in solution spaces using destroy and repair operators. Determining the best operators for LNS to solve a problem at hand is a labor-intensive process. Hence, Adaptive Large Neighborhood Search (ALNS) has been proposed to adaptively select operators during the search process based on operator performances of the previous search iterations. Such an operator selection procedure is a heuristic, based on domain knowledge, which is ineffective with complex, large solution spaces. In this paper, we address the problem of selecting operators for each search iteration of ALNS as a sequential decision problem and propose a Deep Reinforcement Learning based method called Deep Reinforced Adaptive Large Neighborhood Search. As such, the proposed method aims to learn based on the state of the search which operation to select to obtain a high long-term reward, i.e., a good solution to the underlying optimization problem. The proposed method is evaluated on a time-dependent orienteering problem with stochastic weights and time windows. Results show that our approach effectively learns a strategy that adaptively selects operators for large neighborhood search, obtaining competitive results compared to a state-of-the-art machine learning approach while trained with much fewer observations on small-sized problem instances.

Learning Adaptive Evolutionary Computation for Solving Multi-Objective Optimization Problems

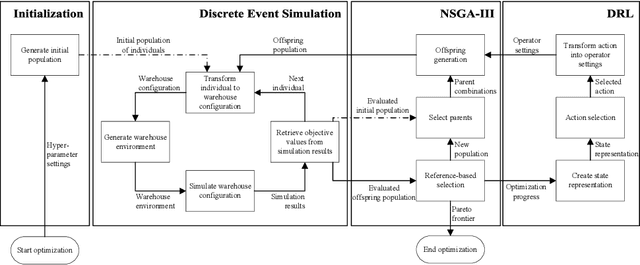
Multi-objective evolutionary algorithms (MOEAs) are widely used to solve multi-objective optimization problems. The algorithms rely on setting appropriate parameters to find good solutions. However, this parameter tuning could be very computationally expensive in solving non-trial (combinatorial) optimization problems. This paper proposes a framework that integrates MOEAs with adaptive parameter control using Deep Reinforcement Learning (DRL). The DRL policy is trained to adaptively set the values that dictate the intensity and probability of mutation for solutions during optimization. We test the proposed approach with a simple benchmark problem and a real-world, complex warehouse design and control problem. The experimental results demonstrate the advantages of our method in terms of solution quality and computation time to reach good solutions. In addition, we show the learned policy is transferable, i.e., the policy trained on a simple benchmark problem can be directly applied to solve the complex warehouse optimization problem, effectively, without the need for retraining.