Using Time-Series Privileged Information for Provably Efficient Learning of Prediction Models

We study prediction of future outcomes with supervised models that use privileged information during learning. The privileged information comprises samples of time series observed between the baseline time of prediction and the future outcome; this information is only available at training time which differs from the traditional supervised learning. Our question is when using this privileged data leads to more sample-efficient learning of models that use only baseline data for predictions at test time. We give an algorithm for this setting and prove that when the time series are drawn from a non-stationary Gaussian-linear dynamical system of fixed horizon, learning with privileged information is more efficient than learning without it. On synthetic data, we test the limits of our algorithm and theory, both when our assumptions hold and when they are violated. On three diverse real-world datasets, we show that our approach is generally preferable to classical learning, particularly when data is scarce. Finally, we relate our estimator to a distillation approach both theoretically and empirically.

EXPObench: Benchmarking Surrogate-based Optimisation Algorithms on Expensive Black-box Functions

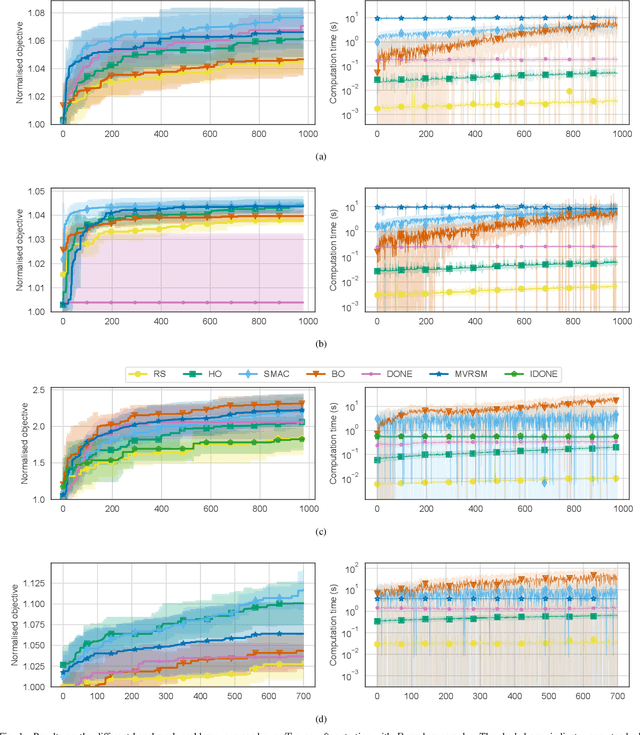
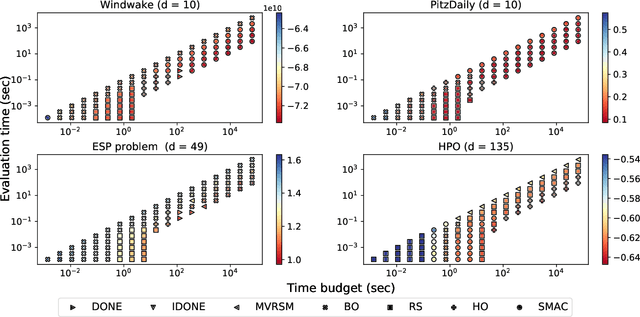
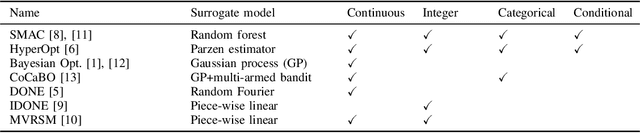
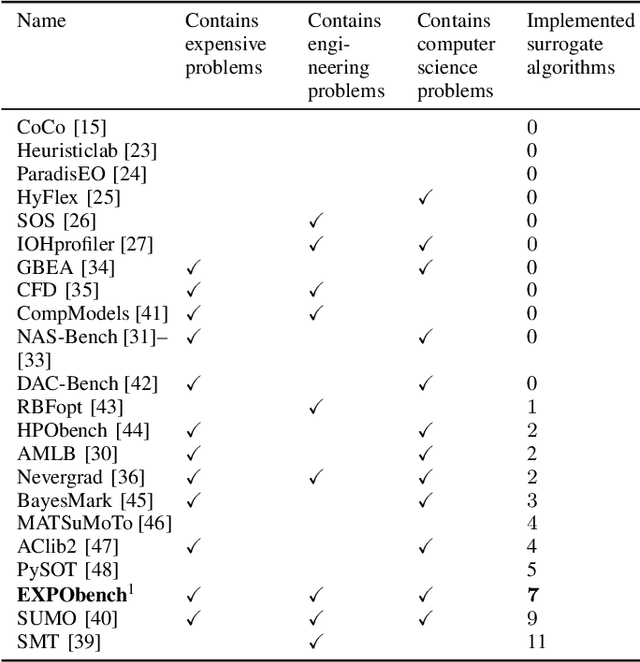
Surrogate algorithms such as Bayesian optimisation are especially designed for black-box optimisation problems with expensive objectives, such as hyperparameter tuning or simulation-based optimisation. In the literature, these algorithms are usually evaluated with synthetic benchmarks which are well established but have no expensive objective, and only on one or two real-life applications which vary wildly between papers. There is a clear lack of standardisation when it comes to benchmarking surrogate algorithms on real-life, expensive, black-box objective functions. This makes it very difficult to draw conclusions on the effect of algorithmic contributions. A new benchmark library, EXPObench, provides first steps towards such a standardisation. The library is used to provide an extensive comparison of six different surrogate algorithms on four expensive optimisation problems from different real-life applications. This has led to new insights regarding the relative importance of exploration, the evaluation time of the objective, and the used model. A further contribution is that we make the algorithms and benchmark problem instances publicly available, contributing to more uniform analysis of surrogate algorithms. Most importantly, we include the performance of the six algorithms on all evaluated problem instances. This results in a unique new dataset that lowers the bar for researching new methods as the number of expensive evaluations required for comparison is significantly reduced.

Continuous surrogate-based optimization algorithms are well-suited for expensive discrete problems

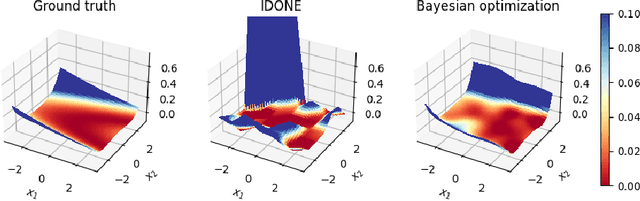
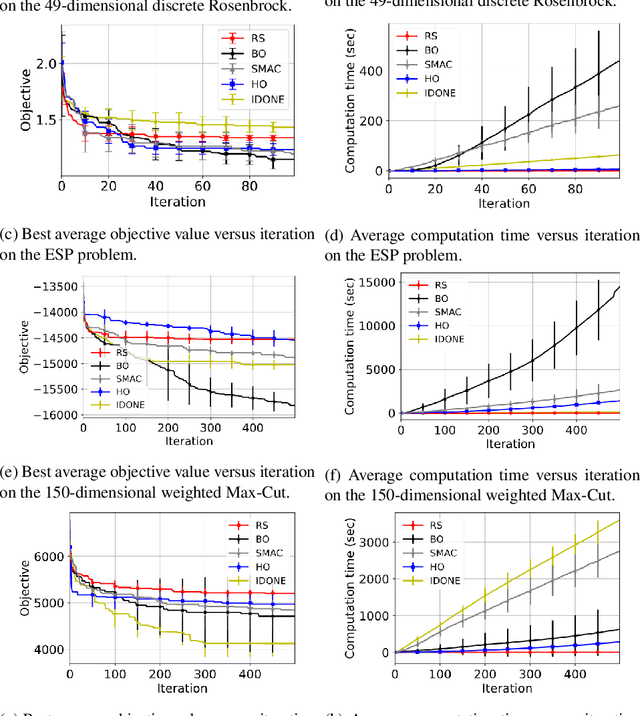
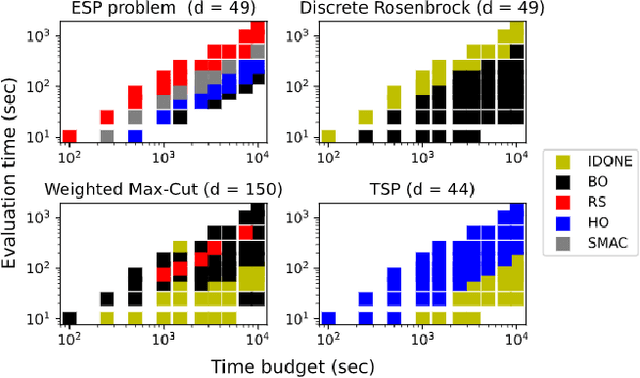
One method to solve expensive black-box optimization problems is to use a surrogate model that approximates the objective based on previous observed evaluations. The surrogate, which is cheaper to evaluate, is optimized instead to find an approximate solution to the original problem. In the case of discrete problems, recent research has revolved around surrogate models that are specifically constructed to deal with discrete structures. A main motivation is that literature considers continuous methods, such as Bayesian optimization with Gaussian processes as the surrogate, to be sub-optimal (especially in higher dimensions) because they ignore the discrete structure by e.g. rounding off real-valued solutions to integers. However, we claim that this is not true. In fact, we present empirical evidence showing that the use of continuous surrogate models displays competitive performance on a set of high-dimensional discrete benchmark problems, including a real-life application, against state-of-the-art discrete surrogate-based methods. Our experiments on different discrete structures and time constraints also give more insight into which algorithms work well on which type of problem.