In-sector Compressive Beam Alignment for MmWave and THz Radios

Beam alignment is key in enabling millimeter wave and terahertz radios to achieve their capacity. Due to the use of large arrays in these systems, the common exhaustive beam scanning results in a substantial training overhead. Prior work has addressed this issue, by developing compressive sensing (CS)-based methods which exploit channel sparsity to achieve faster beam alignment. Unfortunately, standard CS techniques employ wide beams and suffer from a low signal-to-noise ratio (SNR) in the channel measurements. To solve this challenge, we develop an IEEE 802.11ad/ay compatible technique that takes an in-sector approach for CS. In our method, the angle domain channel is partitioned into several sectors, and the channel within the best sector is estimated for beam alignment. The essence of our framework lies in the construction of a low-resolution beam codebook to identify the best sector and in the design of the CS matrix for in-sector channel estimation. Our beam codebook illuminates distinct non-overlapping sectors and can be realized with low-resolution phased arrays. We show that the proposed codebook results in a higher received SNR than the state-of-the-art sector sweep codebooks. Furthermore, our optimized CS matrix achieves a better in-sector channel reconstruction than comparable benchmarks.

Analysis of Orthogonal Matching Pursuit for Compressed Sensing in Practical Settings

Orthogonal matching pursuit (OMP) is a widely used greedy algorithm for sparse signal recovery in compressed sensing (CS). Prior work on OMP, however, has only provided reconstruction guarantees under the assumption that the columns of the CS matrix have equal norms, which is unrealistic in many practical CS applications due to hardware constraints. In this paper, we derive sparse recovery guarantees with OMP, when the CS matrix has unequal column norms. Finally, we show that CS matrices whose column norms are comparable achieve tight guarantees for the successful recovery of the support of a sparse signal and a low mean squared error in the estimate.

Structured Sensing Matrix Design for In-sector Compressed mmWave Channel Estimation

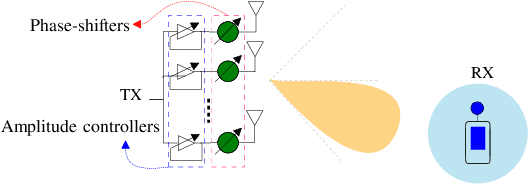
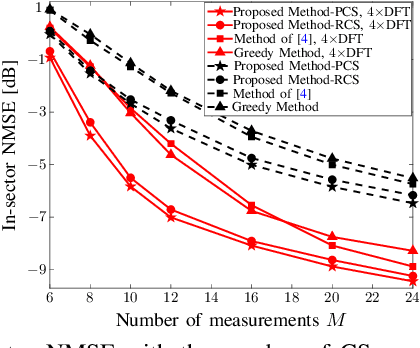
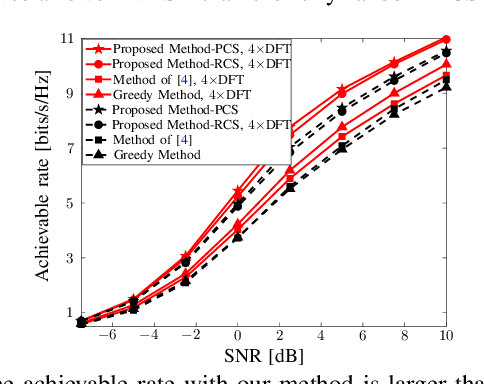
Fast millimeter wave (mmWave) channel estimation techniques based on compressed sensing (CS) suffer from low signal-to-noise ratio (SNR) in the channel measurements, due to the use of wide beams. To address this problem, we develop an in-sector CS-based mmWave channel estimation technique that focuses energy on a sector in the angle domain. Specifically, we construct a new class of structured CS matrices to estimate the channel within the sector of interest. To this end, we first determine an optimal sampling pattern when the number of measurements is equal to the sector dimension and then use its subsampled version in the sub-Nyquist regime. Our approach results in low aliasing artifacts in the sector of interest and better channel estimates than benchmark algorithms.

Nonuniform Defocus Removal for Image Classification

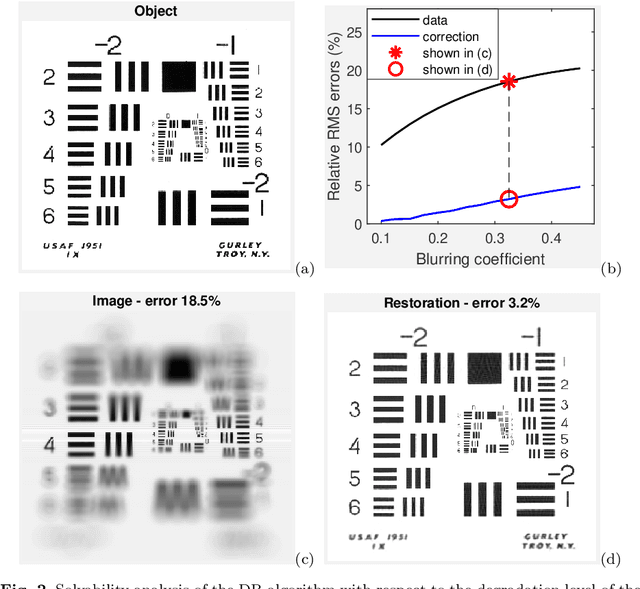
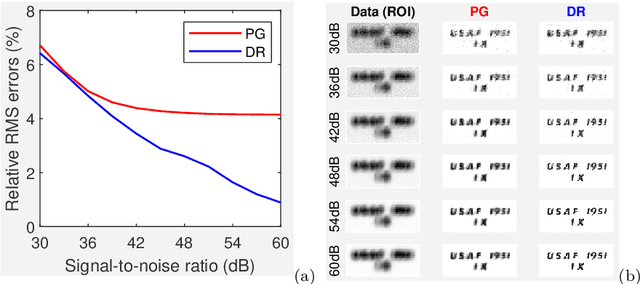
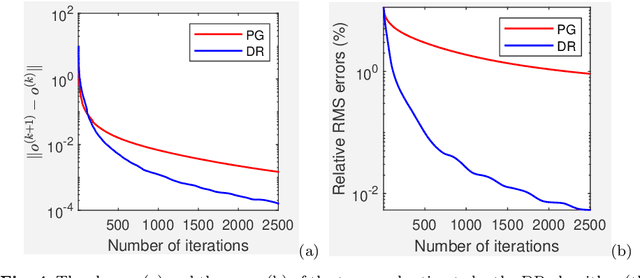
We propose and study the single-frame anisoplanatic deconvolution problem associated with image classification using machine learning algorithms, named the nonuniform defocus removal (NDR) problem. Mathematical analysis of the NDR problem is done and the so-called defocus removal (DR) algorithm for solving it is proposed. Global convergence of the DR algorithm is established without imposing any unverifiable assumption. Numerical results on simulation data show significant features of DR including solvability, noise robustness, convergence, model insensitivity and computational efficiency. Physical relevance of the NDR problem and practicability of the DR algorithm are tested on experimental data. Back to the application that originally motivated the investigation of the NDR problem, we show that the DR algorithm can improve the accuracy of classifying distorted images using convolutional neural networks. The key difference of this paper compared to most existing works on single-frame anisoplanatic deconvolution is that the new method does not require the data image to be decomposable into isoplanatic subregions. Therefore, solution approaches partitioning the image into isoplanatic zones are not applicable to the NDR problem and those handling the entire image such as the DR algorithm need to be developed and analyzed.

System Identification through Online Sparse Gaussian Process Regression with Input Noise

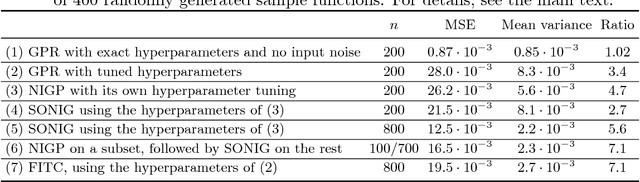
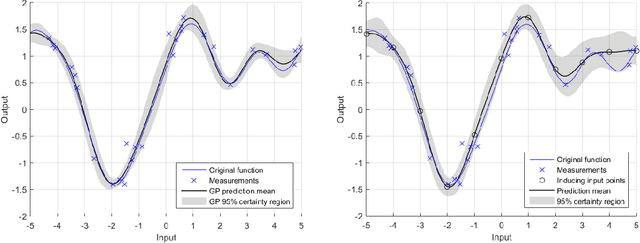
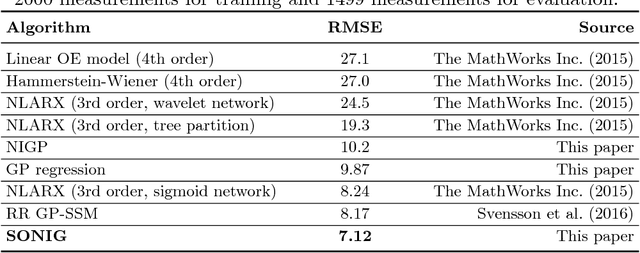
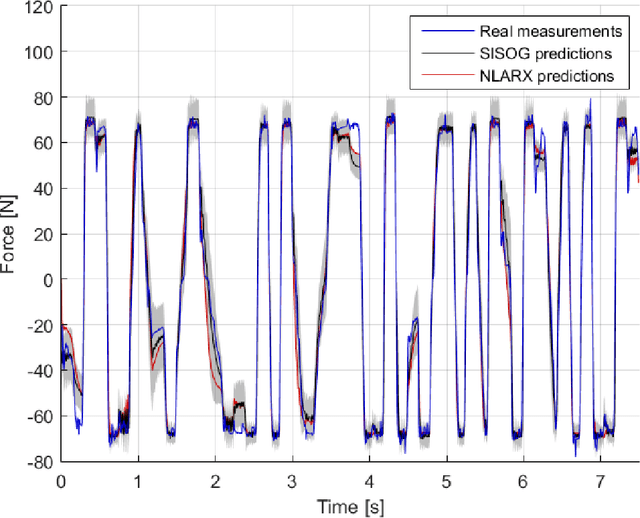
There has been a growing interest in using non-parametric regression methods like Gaussian Process (GP) regression for system identification. GP regression does traditionally have three important downsides: (1) it is computationally intensive, (2) it cannot efficiently implement newly obtained measurements online, and (3) it cannot deal with stochastic (noisy) input points. In this paper we present an algorithm tackling all these three issues simultaneously. The resulting Sparse Online Noisy Input GP (SONIG) regression algorithm can incorporate new noisy measurements in constant runtime. A comparison has shown that it is more accurate than similar existing regression algorithms. When applied to non-linear black-box system modeling, its performance is competitive with existing non-linear ARX models.

A sequential Monte Carlo approach to Thompson sampling for Bayesian optimization

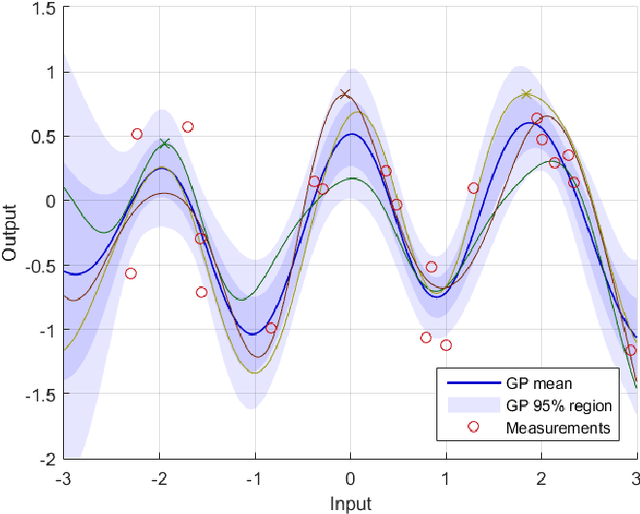
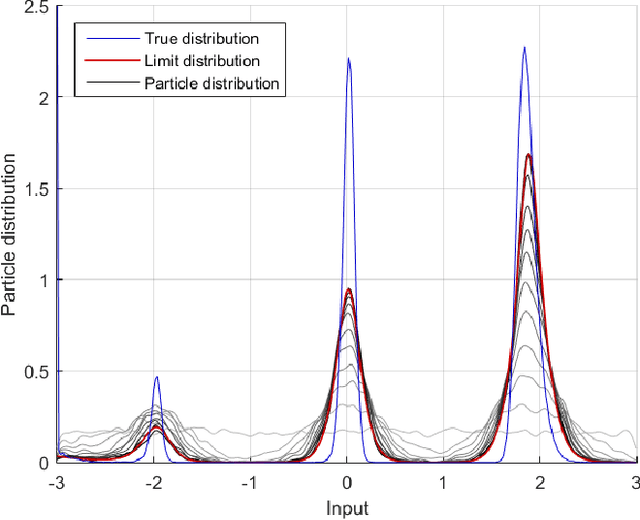
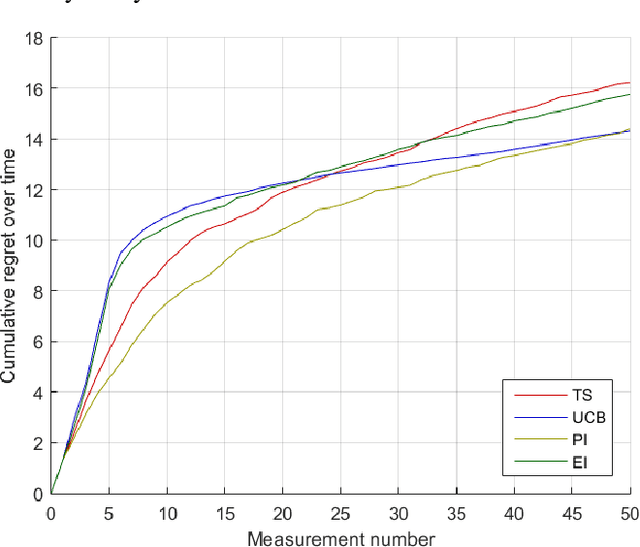
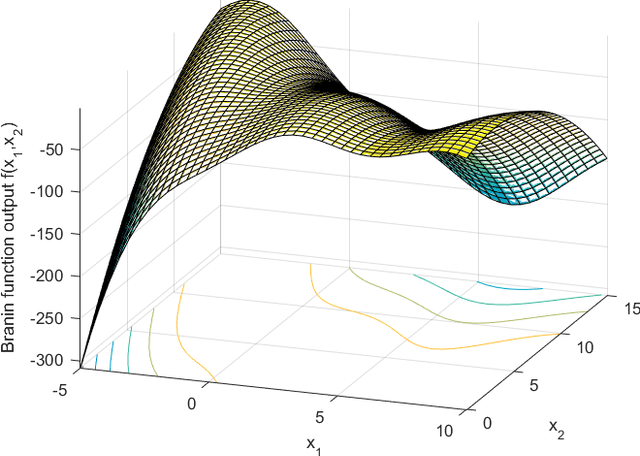
Bayesian optimization through Gaussian process regression is an effective method of optimizing an unknown function for which every measurement is expensive. It approximates the objective function and then recommends a new measurement point to try out. This recommendation is usually selected by optimizing a given acquisition function. After a sufficient number of measurements, a recommendation about the maximum is made. However, a key realization is that the maximum of a Gaussian process is not a deterministic point, but a random variable with a distribution of its own. This distribution cannot be calculated analytically. Our main contribution is an algorithm, inspired by sequential Monte Carlo samplers, that approximates this maximum distribution. Subsequently, by taking samples from this distribution, we enable Thompson sampling to be applied to (armed-bandit) optimization problems with a continuous input space. All this is done without requiring the optimization of a nonlinear acquisition function. Experiments have shown that the resulting optimization method has a competitive performance at keeping the cumulative regret limited.

Online Optimization with Costly and Noisy Measurements using Random Fourier Expansions

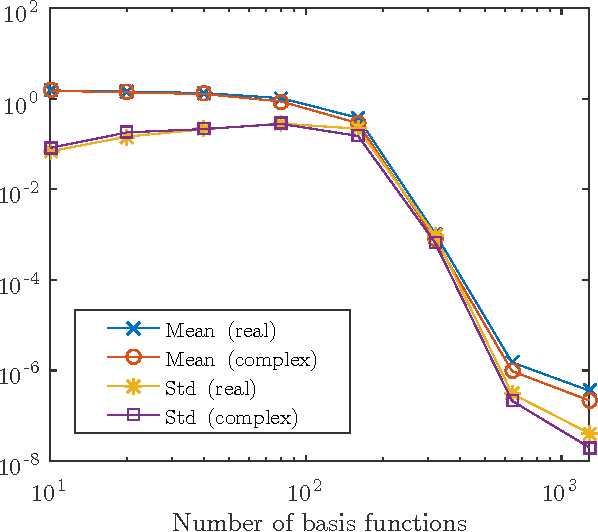
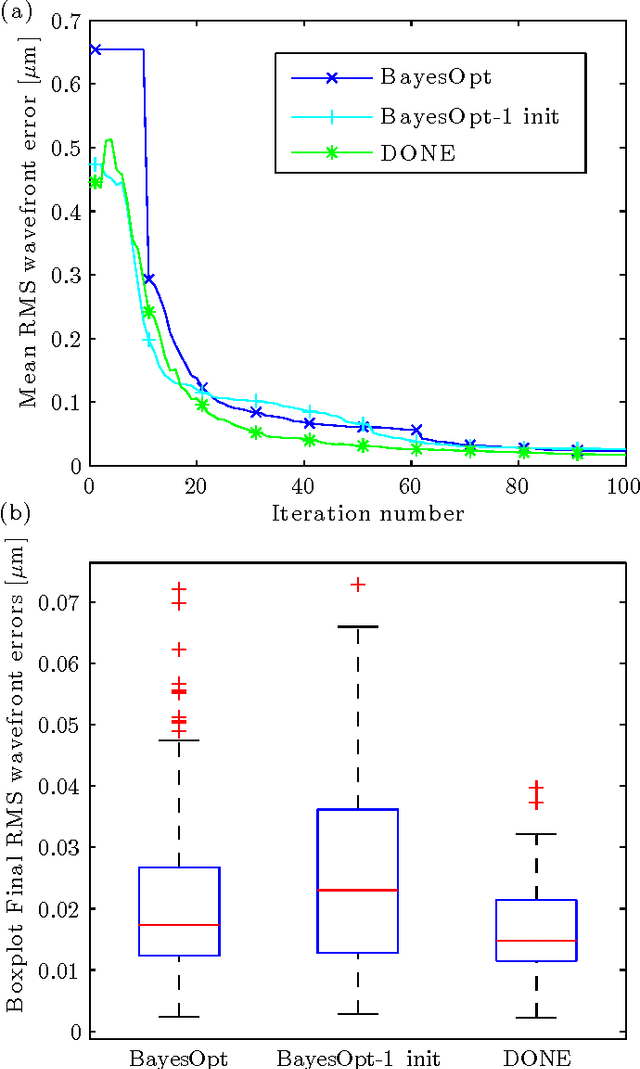
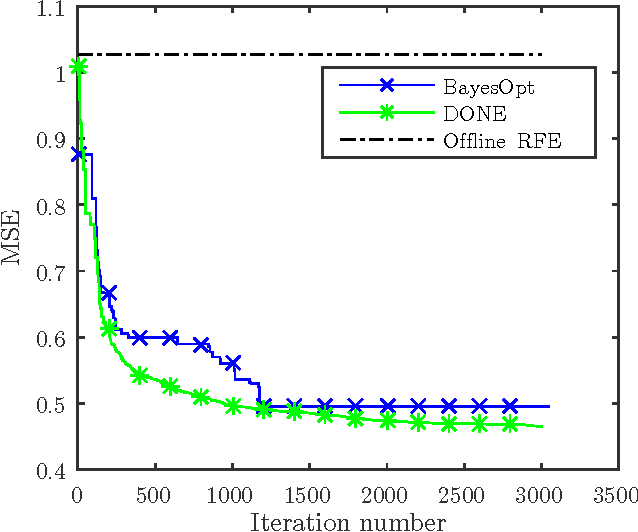
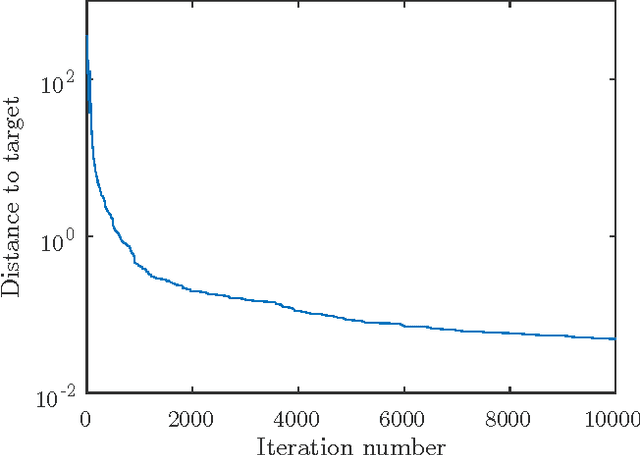
This paper analyzes DONE, an online optimization algorithm that iteratively minimizes an unknown function based on costly and noisy measurements. The algorithm maintains a surrogate of the unknown function in the form of a random Fourier expansion (RFE). The surrogate is updated whenever a new measurement is available, and then used to determine the next measurement point. The algorithm is comparable to Bayesian optimization algorithms, but its computational complexity per iteration does not depend on the number of measurements. We derive several theoretical results that provide insight on how the hyper-parameters of the algorithm should be chosen. The algorithm is compared to a Bayesian optimization algorithm for a benchmark problem and three applications, namely, optical coherence tomography, optical beam-forming network tuning, and robot arm control. It is found that the DONE algorithm is significantly faster than Bayesian optimization in the discussed problems, while achieving a similar or better performance.

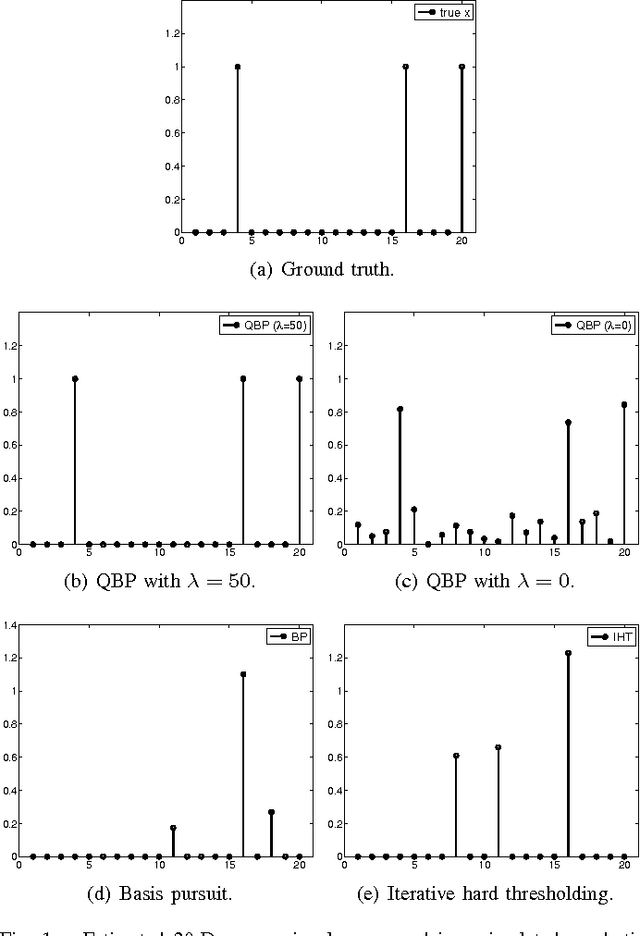
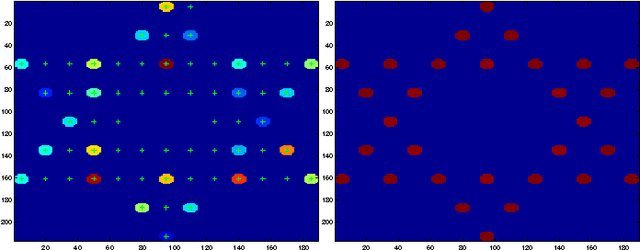
Quadratic Basis Pursuit

In many compressive sensing problems today, the relationship between the measurements and the unknowns could be nonlinear. Traditional treatment of such nonlinear relationships have been to approximate the nonlinearity via a linear model and the subsequent un-modeled dynamics as noise. The ability to more accurately characterize nonlinear models has the potential to improve the results in both existing compressive sensing applications and those where a linear approximation does not suffice, e.g., phase retrieval. In this paper, we extend the classical compressive sensing framework to a second-order Taylor expansion of the nonlinearity. Using a lifting technique and a method we call quadratic basis pursuit, we show that the sparse signal can be recovered exactly when the sampling rate is sufficiently high. We further present efficient numerical algorithms to recover sparse signals in second-order nonlinear systems, which are considerably more difficult to solve than their linear counterparts in sparse optimization.