Henrik Ohlsson
Time to Embed: Unlocking Foundation Models for Time Series with Channel Descriptions
May 20, 2025Abstract:Traditional time series models are task-specific and often depend on dataset-specific training and extensive feature engineering. While Transformer-based architectures have improved scalability, foundation models, commonplace in text, vision, and audio, remain under-explored for time series and are largely restricted to forecasting. We introduce $\textbf{CHARM}$, a foundation embedding model for multivariate time series that learns shared, transferable, and domain-aware representations. To address the unique difficulties of time series foundation learning, $\textbf{CHARM}$ incorporates architectural innovations that integrate channel-level textual descriptions while remaining invariant to channel order. The model is trained using a Joint Embedding Predictive Architecture (JEPA), with novel augmentation schemes and a loss function designed to improve interpretability and training stability. Our $7$M-parameter model achieves state-of-the-art performance across diverse downstream tasks, setting a new benchmark for time series representation learning.
Expert-guided Regularization via Distance Metric Learning
Dec 09, 2019



Abstract:High-dimensional prediction is a challenging problem setting for traditional statistical models. Although regularization improves model performance in high dimensions, it does not sufficiently leverage knowledge on feature importances held by domain experts. As an alternative to standard regularization techniques, we propose Distance Metric Learning Regularization (DMLreg), an approach for eliciting prior knowledge from domain experts and integrating that knowledge into a regularized linear model. First, we learn a Mahalanobis distance metric between observations from pairwise similarity comparisons provided by an expert. Then, we use the learned distance metric to place prior distributions on coefficients in a linear model. Through experimental results on a simulated high-dimensional prediction problem, we show that DMLreg leads to improvements in model performance when the domain expert is knowledgeable.
Finding sparse solutions of systems of polynomial equations via group-sparsity optimization
Jul 16, 2014



Abstract:The paper deals with the problem of finding sparse solutions to systems of polynomial equations possibly perturbed by noise. In particular, we show how these solutions can be recovered from group-sparse solutions of a derived system of linear equations. Then, two approaches are considered to find these group-sparse solutions. The first one is based on a convex relaxation resulting in a second-order cone programming formulation which can benefit from efficient reweighting techniques for sparsity enhancement. For this approach, sufficient conditions for the exact recovery of the sparsest solution to the polynomial system are derived in the noiseless setting, while stable recovery results are obtained for the noisy case. Though lacking a similar analysis, the second approach provides a more computationally efficient algorithm based on a greedy strategy adding the groups one-by-one. With respect to previous work, the proposed methods recover the sparsest solution in a very short computing time while remaining at least as accurate in terms of the probability of success. This probability is empirically analyzed to emphasize the relationship between the ability of the methods to solve the polynomial system and the sparsity of the solution.
Sparse phase retrieval via group-sparse optimization
Feb 24, 2014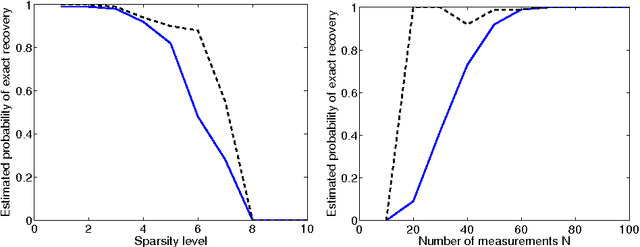
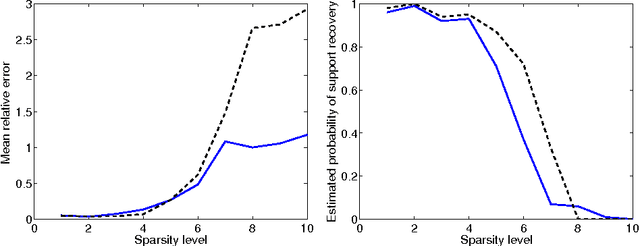
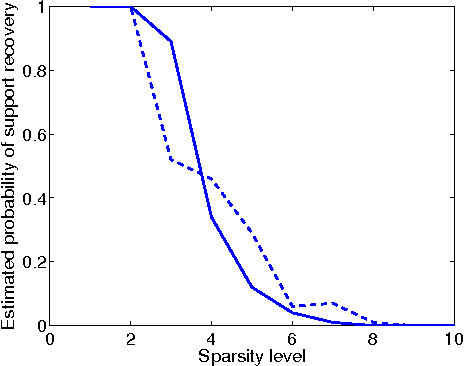
Abstract:This paper deals with sparse phase retrieval, i.e., the problem of estimating a vector from quadratic measurements under the assumption that few components are nonzero. In particular, we consider the problem of finding the sparsest vector consistent with the measurements and reformulate it as a group-sparse optimization problem with linear constraints. Then, we analyze the convex relaxation of the latter based on the minimization of a block l1-norm and show various exact recovery and stability results in the real and complex cases. Invariance to circular shifts and reflections are also discussed for real vectors measured via complex matrices.
Robust Subspace System Identification via Weighted Nuclear Norm Optimization
Dec 07, 2013


Abstract:Subspace identification is a classical and very well studied problem in system identification. The problem was recently posed as a convex optimization problem via the nuclear norm relaxation. Inspired by robust PCA, we extend this framework to handle outliers. The proposed framework takes the form of a convex optimization problem with an objective that trades off fit, rank and sparsity. As in robust PCA, it can be problematic to find a suitable regularization parameter. We show how the space in which a suitable parameter should be sought can be limited to a bounded open set of the two dimensional parameter space. In practice, this is very useful since it restricts the parameter space that is needed to be surveyed.
Scalable Anomaly Detection in Large Homogenous Populations
Sep 20, 2013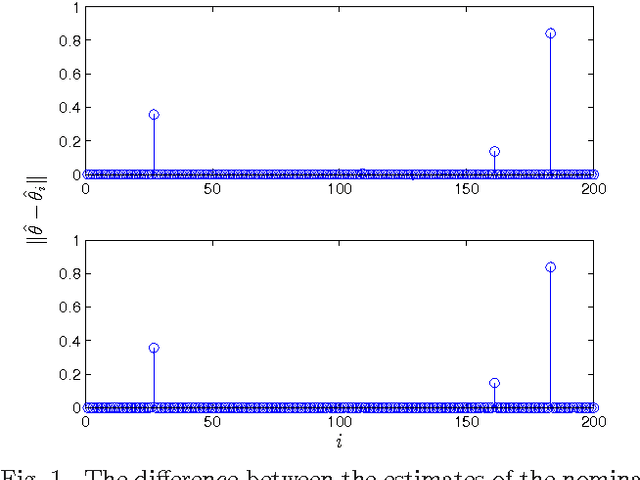
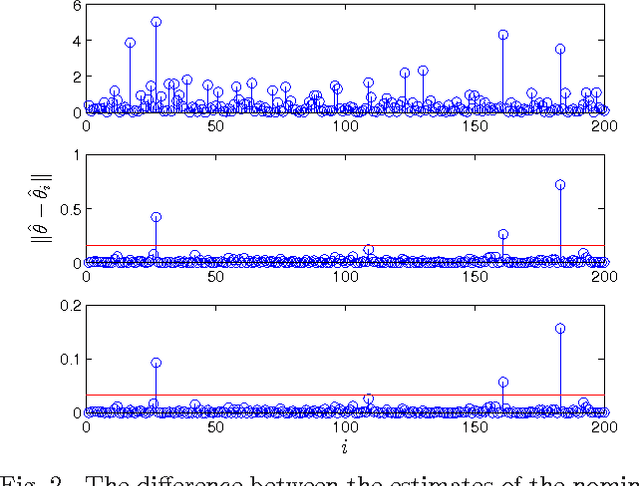
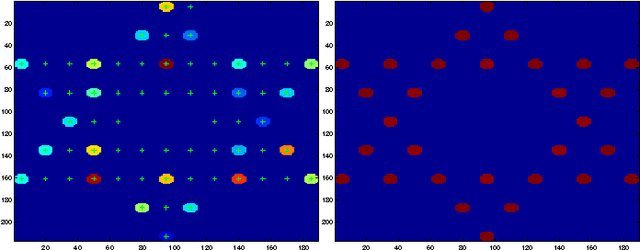
Abstract:Anomaly detection in large populations is a challenging but highly relevant problem. The problem is essentially a multi-hypothesis problem, with a hypothesis for every division of the systems into normal and anomal systems. The number of hypothesis grows rapidly with the number of systems and approximate solutions become a necessity for any problems of practical interests. In the current paper we take an optimization approach to this multi-hypothesis problem. We first observe that the problem is equivalent to a non-convex combinatorial optimization problem. We then relax the problem to a convex problem that can be solved distributively on the systems and that stays computationally tractable as the number of systems increase. An interesting property of the proposed method is that it can under certain conditions be shown to give exactly the same result as the combinatorial multi-hypothesis problem and the relaxation is hence tight.
Compressive Shift Retrieval
Aug 03, 2013



Abstract:The classical shift retrieval problem considers two signals in vector form that are related by a shift. The problem is of great importance in many applications and is typically solved by maximizing the cross-correlation between the two signals. Inspired by compressive sensing, in this paper, we seek to estimate the shift directly from compressed signals. We show that under certain conditions, the shift can be recovered using fewer samples and less computation compared to the classical setup. Of particular interest is shift estimation from Fourier coefficients. We show that under rather mild conditions only one Fourier coefficient suffices to recover the true shift.
Quadratic Basis Pursuit
Feb 09, 2013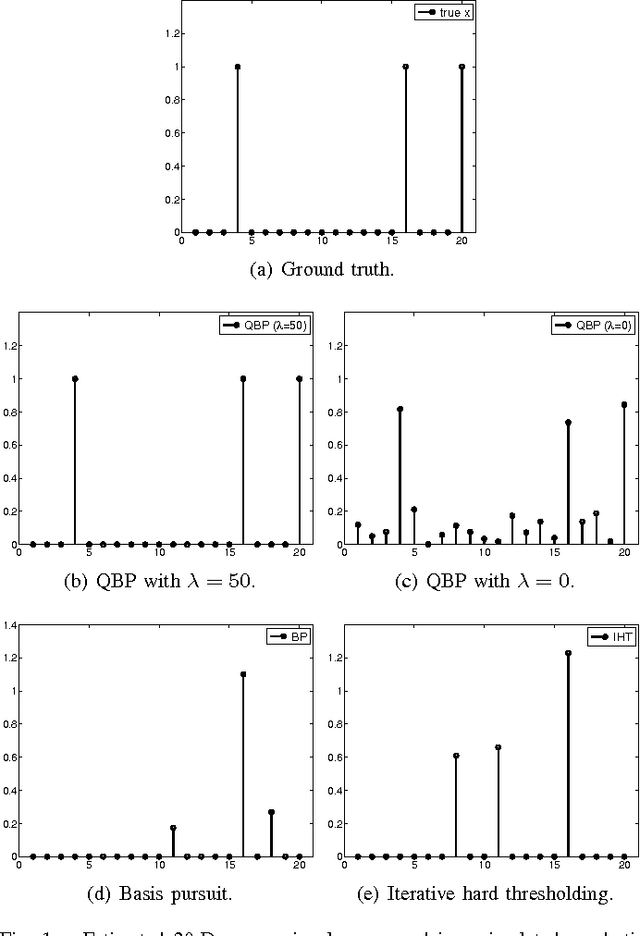


Abstract:In many compressive sensing problems today, the relationship between the measurements and the unknowns could be nonlinear. Traditional treatment of such nonlinear relationships have been to approximate the nonlinearity via a linear model and the subsequent un-modeled dynamics as noise. The ability to more accurately characterize nonlinear models has the potential to improve the results in both existing compressive sensing applications and those where a linear approximation does not suffice, e.g., phase retrieval. In this paper, we extend the classical compressive sensing framework to a second-order Taylor expansion of the nonlinearity. Using a lifting technique and a method we call quadratic basis pursuit, we show that the sparse signal can be recovered exactly when the sampling rate is sufficiently high. We further present efficient numerical algorithms to recover sparse signals in second-order nonlinear systems, which are considerably more difficult to solve than their linear counterparts in sparse optimization.
A Probabilistic Perspective on Gaussian Filtering and Smoothing
Jun 08, 2011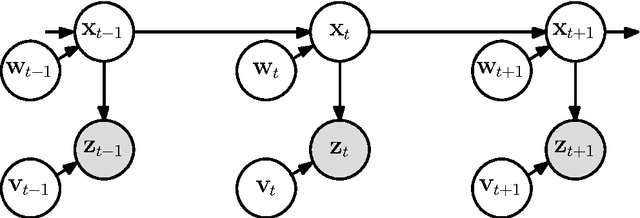
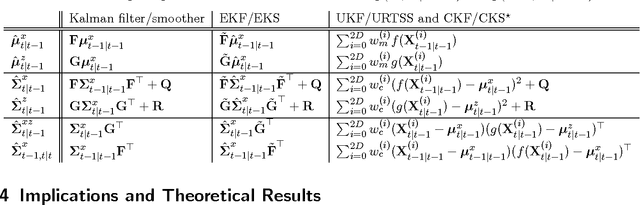

Abstract:We present a general probabilistic perspective on Gaussian filtering and smoothing. This allows us to show that common approaches to Gaussian filtering/smoothing can be distinguished solely by their methods of computing/approximating the means and covariances of joint probabilities. This implies that novel filters and smoothers can be derived straightforwardly by providing methods for computing these moments. Based on this insight, we derive the cubature Kalman smoother and propose a novel robust filtering and smoothing algorithm based on Gibbs sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge