Quadratic Basis Pursuit
Paper and Code
Feb 09, 2013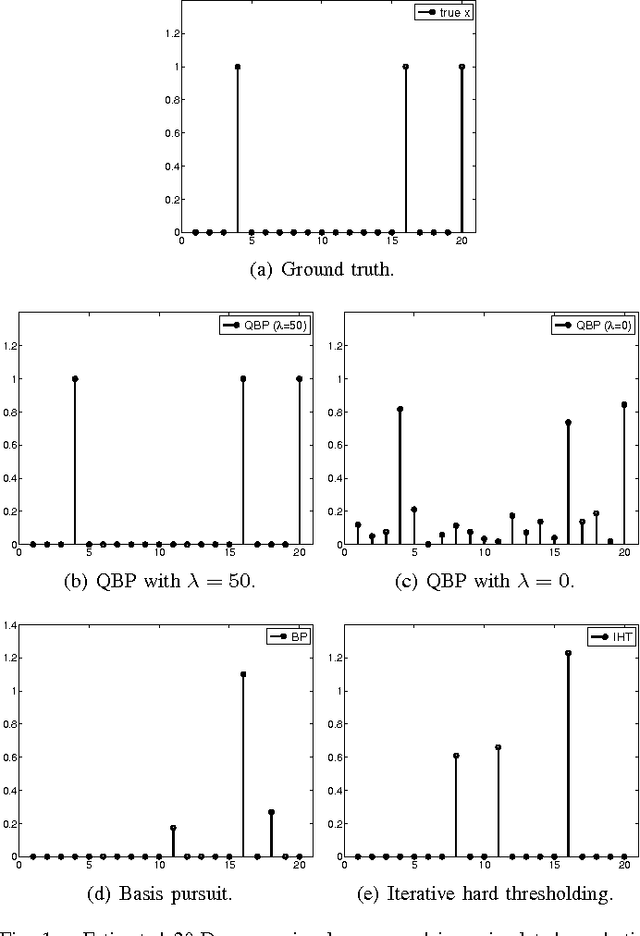


In many compressive sensing problems today, the relationship between the measurements and the unknowns could be nonlinear. Traditional treatment of such nonlinear relationships have been to approximate the nonlinearity via a linear model and the subsequent un-modeled dynamics as noise. The ability to more accurately characterize nonlinear models has the potential to improve the results in both existing compressive sensing applications and those where a linear approximation does not suffice, e.g., phase retrieval. In this paper, we extend the classical compressive sensing framework to a second-order Taylor expansion of the nonlinearity. Using a lifting technique and a method we call quadratic basis pursuit, we show that the sparse signal can be recovered exactly when the sampling rate is sufficiently high. We further present efficient numerical algorithms to recover sparse signals in second-order nonlinear systems, which are considerably more difficult to solve than their linear counterparts in sparse optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge